FUNCIONES MATEMÁTICAS EJERCICIOS RESUELTOS PDF
La función es uno de los conceptos más importantes en matemáticas.
- CLIC AQUÍ Ver PAR ORDENADO EJERCICIOS RESUELTOS
- Ver PRODUCTO CARTESIANO
- Ver SISTEMA BIDIMENSIONAL
- Ver RELACIONES
- Ver CORRESPONDENCIA
- Ver APLICACIÓN
- Ver QUÉ ES UNA FUNCIÓN
- Ver CONDICIÓN DE EXISTENCIA
- Ver REGLA DE CORRESPONDENCIA
- Ver DOMINIO
- Ver RANGO
- Ver LA GRÁFICA - PROPIEDAD GEOMÉTRICA
- Ver FUNCIONES ELEMENTALES
- Ver FUNCIÓN CONSTANTE
- Ver FUNCIÓN IDENTIDAD
- Ver FUNCIÓN VALOR ABSOLUTO
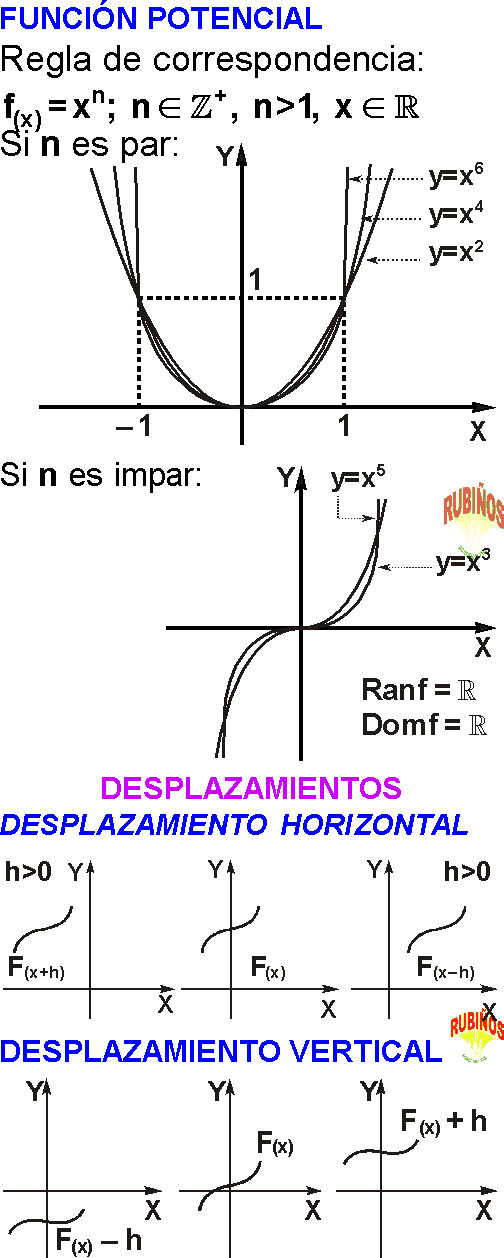
- Ver FUNCIÓN POTENCIAL
- Ver FUNCIÓN RAÍZ CUADRADA
- Ver FUNCIÓN INVERSO MULTIPLICATIVO
- Ver FUNCIÓN ESCALON UNITARIO
- Ver FUNCIÓN SIGNO
- Ver MÁXIMO ENTERO
- Ver FUNCIÓN MÁXIMO ENTERO
- Ver FUNCIÓN LINEAL
- Ver FUNCIÓN AFIN LINEAL
- Ver FUNCIÓN CUADRÁTICA
- Ver FUNCIÓN CÚBICA
- Ver FUNCIÓN POLINOMIAL
- Ver PROPIEDADES DE GRAFICACIÓN
- Ver FUNCIONES NOTABLES
- Ver FUNCIÓN PAR
- Ver FUNCIÓN IMPAR
- Ver FUNCIÓN PERIÓDICA
- Ver FUNCIONES CRECIENTES MONOTONAS
- Ver FUNCIÓN ACOTADA
- Ver FUNCIÓN INYECTIVA
- Ver FUNCIÓN SURYECTIVA
- Ver FUNCIÓN BIYECTIVA
- Ver FUNCIONES TRIGONOMÉTRICAS DIRECTAS
- Ver ÁLGEBRA DE FUNCIONES
- Ver COMPOSICIÓN DE FUNCIONES
- Ver FUNCIÓN INVERSA
- Ver FUNCIONES TRIGONOMÉTRICAS INVERSAS
- Ver MODELACIÓN
- Ver FUNCIÓN EXPONENCIAL
- Ver FUNCIÓN LOGARÍTMICA
- Ver TEORÍA BÁSICA DE FUNCIONES
- Ver PROBLEMAS RESUELTOS
- Ver PRACTICA CON RESPUESTAS
- Ver VIDEOS
PREGUNTA 1 :
Halle la ecuación de la recta cuya gráfica se da a continuación.
A) 2x+3y – 2=0
B) 2x+y – 6=0
C) 2x-3y – 6=0
D) 6x+2y – 3=0
E) 2x+3y – 6=0
RESOLUCIÓN :
Sea la ecuación: y=mx+b , donde b=2. Entonces, y=mx+2, luego reemplazando el punto (3;0) en la función, se tiene que x= – 2/3
Luego y= – 2/3x + 2
Que despejando es equivalente a 2x+3y – 6=0
Rpta. : "E"
PREGUNTA 2 :
Sea F(x) una función lineal en la cual se verifica:
• F(0) + F(1) = 3
• 3F(1) – F(0) = 13
Halle F( – 2).
A) 11
B) 12
C) –11
D) 13
E) 10
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 3 :
Dada la función cuadrática F que corta al eje de las abscisas en los puntos (5;0) y ( – 1;0), halle el punto de corte con el eje de las ordenadas, sabiendo que el mínimo valor que toma la función es – 3.
A) (0;–1/3)
B) (0; –3/2)
C) (0;1/2)
D) (0;– 1/4)
E) (0;– 5/3)
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 4 :
Se conoce la siguiente función lineal:
f(x)=Ax+B
De modo que los pares ordenados (3;7), (a – 1; a – 1) y (a; a – 3) pertenecen a dicha función.
Halle A+B.
A) 10
B) 11
C) 12
D) 13
E) 9
RESOLUCIÓN :
Dada la función f(x)=Ax+B
Como (3;7)∈ f ⇒ 3A+B=7 ... (I)
(a – 1; a – 1)∈ f ⇒ (a – 1)A+B= a – 1 ... (II)
(a; a – 3)∈ f ⇒ aA+B= a – 3 ... (III)
De (II) y (III) se tiene: A= – 2
Luego; en (I): 3(– 2)+B=7
⇒ B=13
Finalmente: A+B=11
Rpta. : "B"
PREGUNTA 5 :
Siendo F una función lineal tal que (1;2) y (4;6) son coordenadas que pertenecen a la función F y G(x)=– 2x+3, calcule la suma de las pendientes de las funciones lineales F y G.
A) –1/3
B) – 2/3
C) 1/5
D) 1/3
E) 2/5
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 6 :
Halle el rango de la función F: ℝ → ℝ, cuya regla de correspondencia es:
F(x)= – x2+4x
A) ] – ∞;+2]
B) [4; ∞[
C) ] – 4;+∞[
D) ] – ∞; – 4]
E) ] – ∞;+4]
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 7 :
Dada la siguiente gráfica de la función “F”
¿Cuántas de las siguientes proposiciones son verdaderas?
I. El rango de f es [ – 3;3[
II. La pendiente de f es – 3 en el intervalo ]0;3[
III. f(8) – f( – 8)=0
A) Solo I
B) Solo II
C) Solo III
D) Ninguna
E) Todas
RESOLUCIÓN :
I. (F), el rango es [ – 3;3]
II. (F), la recta está inclinada hacia la derecha en el intervalo ]0;3[ debe ser positiva
III. (F), f(8)=3 f( – 8)= – 3
⇒ f(8) – f( – 8)=6
Rpta. : "D"
Por largo tiempo, los matemáticos y cientificos buscaron una forma precisa de describir las relaciones que pueden existir entre dos variables. Resulta sorprendente que esta idea haya tardado tanto tiempo en cristalizar en un concepto claro y no ambiguo.
Al matemático francés P.G. Lejeune Dirichet (1805-1859) se le otorga el reconocimiento de la definición moderna de función. Una función es una regla que asigna a cada elemento de un conjunto (llamado el dominio de la función) exactamente un valor de otro conjunto.
El conjunto de todos los valores asignados se llama el rango de la función: Tres ejemplos ayudarán aclarar esta idea. Cuando un comerciante pone una etiqueta con el precio de venta de cada una de las peras, queda determinada una función el dominio es el conjunto de sandías, el rango es el conjunto de precios y la regla es el procedimiento que utiliza el comerciante para asignar precios (quizá una cantidad específica por kilo).
Cuando un profesor asigna una calificación a cada estudiante de una clase, está determinado una función.
El dominio es el conjunto de estudiantes y el rango el conjunto de calificaciones, pero ¿cuál es la regla? Esta cambia de profesor a profesor; algunos, prefieren mantenerla en secreto.
EJEMPLOS DE LAS FUNCIONES MATEMÁTICAS EN LA VIDA DIARIA
• Función lineal
Ejemplo:
El costo total de un viaje en taxi.
Aplicación:
Si una bajada de bandera cuesta $3 y cada kilómetro cuesta $2, la función sería: Costo(x) = 2x + 3, donde x es la cantidad de kilómetros.
• Función cuadrática
Ejemplo:
Trayectoria de un balón al patearlo.
Aplicación:
Al lanzar un balón, su trayectoria forma una parábola. La altura del balón según el tiempo sigue una función cuadrática.
• Función exponencial
Ejemplo:
Crecimiento de una población o interés compuesto en una cuenta de banco.
• Función inversa
Ejemplo:
Velocidad y tiempo de viaje.
Aplicación:
Si vas a una velocidad más alta, tardas menos tiempo. El tiempo es una función inversa de la velocidad: Tiempo(v) = Distancia / v
Función logarítmica
Ejemplo:
Escala Richter de terremotos o nivel de pH.
Aplicación:
Un terremoto de magnitud 6 es 10 veces más fuerte que uno de magnitud 5. El logaritmo mide cómo varía la magnitud con cada incremento.
• Función trigonométrica
Ejemplo:
Movimiento de una rueda o la marea.
Aplicación:
La posición de una rueda que gira o el nivel de agua por las mareas sigue patrones senoidales.
LA HISTORIA DE LAS FUNCIONES MATEMÁTICAS
1. ORÍGENES ANTIGUOS (EGIPTO, BABILONIA Y GRECIA)
Aunque no tenían el concepto formal de "función", ya usaban relaciones entre variables. Por ejemplo, los babilonios sabían cómo calcular el área de figuras geométricas, lo cual implicaba una relación entre medidas.
2. EDAD MEDIA Y MUNDO ISLÁMICO
Matemáticos islámicos como al-Khwarizmi (siglo IX) desarrollaron métodos algebraicos que implicaban relaciones entre cantidades, base de futuras funciones.
3. SIGLO XVII – NACIMIENTO DEL CÁLCULO
René Descartes introdujo el plano cartesiano, permitiendo representar funciones como curvas en un gráfico. Isaac Newton y Gottfried Leibniz desarrollaron el cálculo diferencial e integral, donde las funciones se volvieron fundamentales para describir cambios y movimientos.
4. SIGLO XVIII – FORMALIZACIÓN DEL CONCEPTO
Matemáticos como Leonhard Euler comenzaron a usar la notación f(x) para representar funciones. Se clasificaron funciones (lineales, polinómicas, trigonométricas, etc.) y se estudiaron sus propiedades.
5. SIGLO XIX – RIGOR MATEMÁTICO
Con Augustin Cauchy y Karl Weierstrass, se definió el concepto de función con más rigor. Se introdujeron funciones más generales y abstractas, como las funciones discontinuas.
6. SIGLO XX HASTA HOY – FUNCIONES EN TODAS PARTES
Las funciones se usan en física, estadística, informática, economía, biología, etc. Surgen funciones computables, funciones de varias variables y funciones en espacios abstractos (como en álgebra y análisis funcional).
¿QUÉ ES UNA FUNCIÓN (EN TÉRMINOS MODERNOS)?
Una función es una regla que asigna a cada elemento de un conjunto (dominio) exactamente un elemento de otro conjunto (codominio).