FUNCIONES SURYECTIVAS SOBREYECTIVA EPIYECTIVAS EJERCICIOS RESUELTOS
función sobreyectiva o suryectiva :
Se dice que una función es sobreyectiva cuando todos los elementos del conjunto de llegada (B) son imagen de algún elemento del conjunto de partida (A).
Esto equivale afirmar que es sobreyectiva la función cuyo rango es igual al conjunto de llegada. Cuando una función sobreyectiva se expresa en forma de pares ordenados, se observa que todos los elementos del conjunto de llegada aparecen, al menos una vez, como segunda componente de algún par.
DEFINICIÓN :
Una función f : es suryectiva (sobreyectiva o epiyectiva) si todo elemento del conjunto de llegada es imagen de , por lo menos, un elemento del dominio de f .
Es decir :
Existe sobreyección , si todos los elementos de Y tienen su preimagen en el conjunto de partida X , con la alternativa de que un elemento de Y puede ser imagen de varios elementos de X.
Ejemplos :
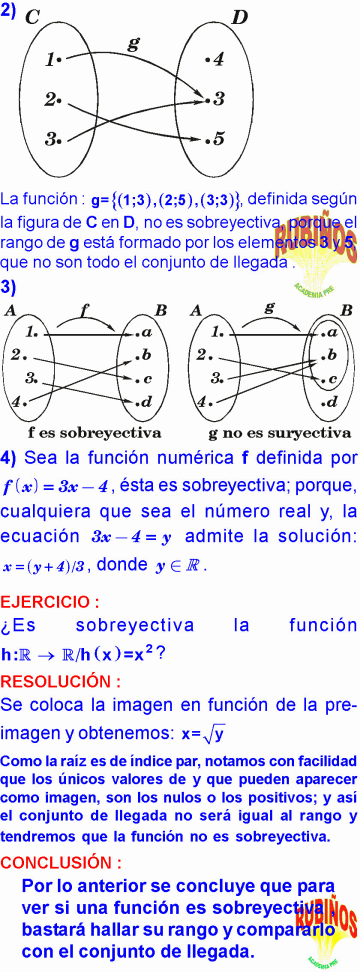
La función , definida de A en B según la figura es sobreyectiva , porque el rango de «f» está formado por el conjunto , que es todo el conjunto de llegada.
La función : , definida según la figura de C en D, no es sobreyectiva, porque el rango de g está formado por los elementos 3 y 5, que no son todo el conjunto de llegada . 3) 4) Sea la función numérica f definida por , ésta es sobreyectiva; porque, cualquiera que sea el número real y, la ecuación admite la solución: , donde . ejercicio :
¿Es sobreyectiva la función ?
Resolución : Se coloca la imagen en función de la pre-imagen y obtenemos:
Como la raíz es de índice par, notamos con facilidad que los únicos valores de y que pueden aparecer como imagen, son los nulos o los positivos; y así el conjunto de llegada no será igual al rango y tendremos que la función no es sobreyectiva.
CONCLUSIÓN :
Por lo anterior se concluye que para ver si una función es sobreyectiva , bastará hallar su rango y compararlo con el conjunto de llegada. Interpretación Gráfica : nota : Sea f : suryectiva con A y B conjuntos finitos , entonces : En aquellas funciones donde no se indica el conjunto de llegada, se les considera suryectiva. Ejercicio 1 : Sea la función f: , definida por Averigue si f es sobreyectiva. Resolución : Para que f sea sobreyectiva debe cumplirse que . Hallemos el Rango de f , como Luego Por tanto , f no es sobreyectiva Ejercicio 2 : Averiguar si : f: es sobreyectiva con Resolución : Ejercicio 3: Si f: es una función decreciente (estrictamente decreciente) y suryectiva tal que y f(0)= – a. Hallar b – a. Resolución : Como f es suryectiva como f es decreciente : f(1) = 2 ¿por qué? Resolvemos : Piden : b – a = 8 – (– 4) = 12 Ejercicio 4 : La función f: con es sobreyectiva (suryectiva), entonces se pide hallar B Resolución : ¿por qué? Como f es suryectiva nota : Toda función f es sobreyectiva sobre su rango.