MATEMÁTICA RECREATIVA EJERCICIOS RESUELTOS 2025 PDF

Los ejercicios que se proponen en las situaciones lógicas recreativas aportan diversión y desarrollo del pensamiento creativo. 
Para dar con las respuestas deberemos previamente plantearnos preguntas como: 
¿He comprendido bien el enunciado del problema?
¿he identificado claramente lo que me están pidiendo calcular, encontrar, discernir o resolver? ; entonces
¿ qué estrategia debo aplicar?
¿ qué pasos me conducirán hasta la respuesta?
PREGUNTA 1 : 
¿Cuántos colores como mínimo es necesario usar, para pintar toda la figura, si dos regiones con lados o segmentos de lado en común no deben tener el mismo color? 
A) 5 
B) 2 
C) 3 
D) 4 
E) 6 
RESOLUCIÓN :
La disposición de los colores se describe en la figura 
Rpta. : "D"
PREGUNTA 2 : 
Rosy tiene como tarea pintar la figura mostrada de modo que dos regiones simples con un lado o parte de un lado común no debe tener el mismo color. ¿Cuántos colores como mínimo debe usar? 


A) 2 
B) 3 
C) 4 
D) 5 
RESOLUCIÓN :
En la figura se muestra los cuatro colores que como mínimo se deben usar 
Rpta. : "C"
PREGUNTA 3 : 
¿Cuántos colores como mínimo es necesario usar, para pintar toda la figura, si dos regiones con lados o segmentos de lado en común no deben tener el mismo color? 
A) 2 
B) 3 
C) 4 
D) 5 
RESOLUCIÓN :
La disposición de los tres colores se describe en la figura 
Rpta. : "B"
PREGUNTA 4 : 
¿Cuántos colores como mínimo se necesitan para colorear un cubo cuyas caras han sido divididas en nueve cuadrados congruentes, de tal manera que dos cuadrados con lados comunes no tengan colores iguales? 
A) 2 
B) 3 
C) 4 
D) 5 
E) 6 
RESOLUCIÓN :
Trabajando en el cubo como en el siguiente gráfico se tiene que se necesitan 3 colores como mínimo. 
Rpta. : "B"
PREGUNTA 5 : 
Se tiene en una caja de cartón de base cuadrada sin tapa y 9 estrellas de cristal. ¿Cuántas cajas de base cuadrada como mínimo debe incluir dentro de dicha caja para que cada estrella este separada de las demás? 
A) 2 
B) 4 
C) 9 
D) 3 
E) 5 
RESOLUCIÓN :
Debe incluirse 2 cajas 
Rpta. : "A"
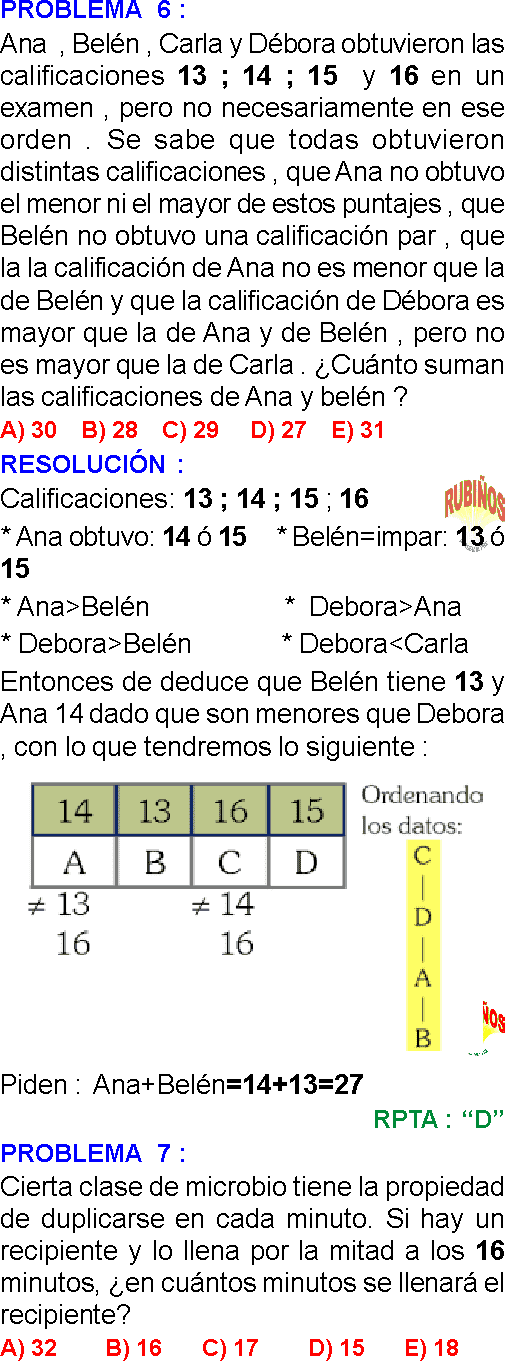
PREGUNTA 6 : 
¿Cuántas líneas rectas necesitarías trazar como mínimo para unir todos los asteriscos mostrados, si no debes levantar el lápiz ni tampoco repasar (si puede cruzar) por alguna línea ya trazada? 
A) 6 
B) 5 
C) 7 
D) 4 
RESOLUCIÓN :
En la figura se muestra la cantidad de líneas que se necesitaría realizar Se necesitaría 6 líneas rectas. 
Rpta. : "A"
PREGUNTA 7 : 
Bety tiene como tarea pintar el cuadro mostrado en la figura de modo que dos regiones simples con un lado (o parte de un lado) común no deben tener el mismo color. ¿Cuántos colores como mínimo debe usar? 
A) 2 
B) 6 
C) 3 
D) 4 
RESOLUCIÓN :
Se usan solo 3 colores. 
Rpta. : "C"
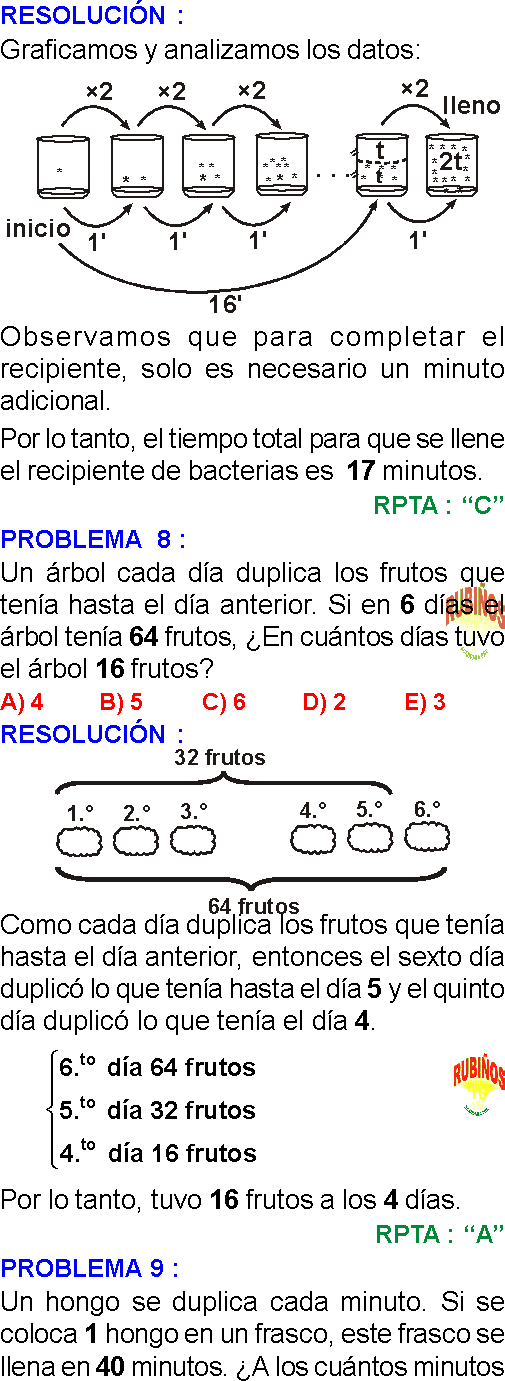
PREGUNTA 8 : 
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 9 : 
En el cuadro adjunto se escriben los números 1; 2; 3 y 4 sin repetición, en cada fila, cada columna y cada diagonal. Determine a – b. 
A) 3 
B) – 3 
C) 2 
D) – 2 
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 10 : 
Empleando cerillos de igual longitud se ha construido triángulos equiláteros, tal como se muestra en la figura. ¿Cuántos cerillos hay que retirar como mínimo para que no quede ninguno de dichos triángulos? 
A) 4 
B) 5 
C) 6 
D) 7 
RESOLUCIÓN :
Es suficiente retirar 6 cerillos Y la figura queda como se indica. 
Rpta. : "C"
PREGUNTA 11 : 
Renato tiene varias fichas de madera como muestra la Figura I y la Figura II, además estas fichas están formadas por cuadraditos de 1 cm de lado. Si quiere formar el cuadrado más pequeño juntando, en igual cantidad ambas fichas y sin dejar espacios vacíos, ¿cuántas fichas, como mínimo en total, utilizará? 
A) 10 
B) 12 
C) 14 
D) 16 
RESOLUCIÓN :
En la figura se muestran las fichas de cada tipo que se necesitan como mínimo 
Total, de fichas que se usan: 6+6 = 12 
Rpta. : "B"
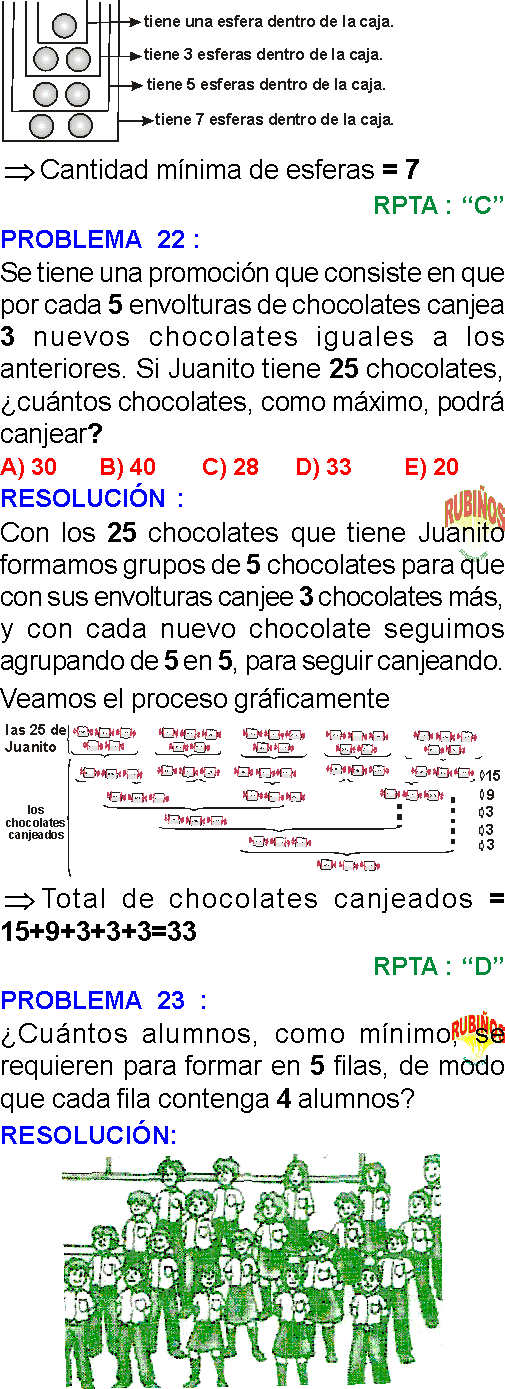
PREGUNTA 12 : 
Elva está muy contenta pues se enteró de la promoción que por cada tres envolturas de galletas vacías, puede canjear una nueva galleta. ¿Cuál es la máxima cantidad de galletas que podrá comer, si ella ha comprado 31 galletas? 
A) 47 
B) 45 
C) 44 
D) 41 
E) 46 
RESOLUCIÓN :
Primero come 31 galletas, le salen 31 envolturas = 10 galletas + 1 envoltura 
Luego come 10 galletas, le salen 10 envolturas = 3 galletas + 1 envoltura 
Luego come 3 galletas, le salen 3 envolturas = 1 galleta 
Luego come 1 galleta, le sale 1 envoltura, juntando con las otras 2 envolturas anteriores, equivale a otra galleta. 
Por lo tanto come como máximo: 31 + 10 + 3 + 1 + 1 = 46 
Rpta. : "E"
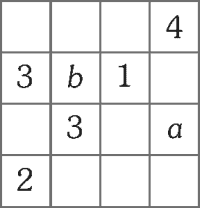
PREGUNTA 13 : 
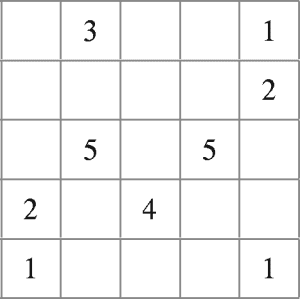
En la figura, se muestra el plano de un terreno, el cual ha sido lotizado en 25 lotes cuadrados con la intención de que en algunos lotes se construyan casas y en los demás, se plante árboles. Los números indican cuántos lotes alrededor de dicho lote se van a destinar para la plantación de árboles. Si en los lotes numerados no se van a sembrar árboles, ¿cuántas casas se construirán en dicho terreno? 
A) 18 
B) 15 
C) 10 
D) 17 
E) 12 
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 14 : 
En la figura se tiene un trozo de madera, el cual puede ser dividido en 12 cubitos. Si solo se desea separar los 3 cubos sombreados, ¿cuántos cortes rectos como mínimo deberá realizarse con una sierra eléctrica? 
A) 2 
B) 3 
C) 4 
D) 5 
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 15: 
Sobre una mesa hay vasos transparentes idénticos en fila: 32 están vacíos y 32 están llenos de vino tinto y en la disposición que muestra la figura. ¿Cuál es el mínimo número de vasos que deben ser movidos para que aparezcan todos los vasos llenos en un lado y todos los vacíos en el otro? 
A) 14    
B) 18    
C) 20    
D) 16
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 16 : 
Un herrero tenía una cadena continua de oro, de 32 eslabones, un día llega a una posada y quiere hacer efectivo el pago de la habitación con la cadena teniendo que pagar por adelantado cada día un eslabón. Para ello decide cortar y soldar algunos eslabones y durante los 32 días que estuvo no hubo ningún problema con el pago, ¿cuántos eslabones como mínimo tuvo que cortar de uno en uno y luego soldar el herrero? 
A) 31 
B) 2 
C) 4 
D) 3 
E) 14 
RESOLUCIÓN :
Hace como mínimo 3 cortes: corta y suelda aparte el eslabón 3, el eslabón 9 y el eslabón 21. 
De tal manera que le quedan: 7 trozos de 1, 1, 1, 2, 5, 11 y 11 eslabones. 
Con estos pedazos pagando de forma adecuada se consigue lo que se pide. 
Rpta. : "B"
PREGUNTA 17 : 
Tom observa sobre una mesa 4 monedas de cinco soles (ver figura). Si empieza a colocar monedas de cinco soles tangencialmente entre sí alrededor de las que están sobre la mesa, ¿cuántas monedas como máximo puede colocar? 
A) 4 
B) 9 
C) 10 
D) 6 
E) 12 
RESOLUCIÓN :
Número de monedas: 10 
Rpta. : "C"
PREGUNTA 18 : 
La figura 1 muestra un recipiente abierto en P, Q y R con cinco bolos numerados. Si una operación consiste en sacar solo un bolo por Q o R e inmediatamente introducirlo por P, ¿cuántas operaciones, como mínimo, se deben realizar con los bolos de la figura 1 para obtener la disposición de bolos de la figura 2? 
A) 5 
B) 8 
C) 4 
D) 7 
E) 3 
RESOLUCIÓN :
Rpta. : "E"

Ejercicios resueltos de examen de admisión a la Universidad