FUNCIONES TRIGONOMÉTRICAS INVERSAS EJERCICIOS RESUELTOS PDF
¿Qué son las funciones trigonométricas inversas?
Una función trigonométrica inversa es un conjunto de pares ordenados de números reales (x;y), en los cuales la primera componente X es el valor de alguna razón trigonométrica y la segunda componente Y es el arco cuya razón trigonométrica es X
☛ Función arco seno o seno inverso
☛ Función arco coseno o coseno inverso
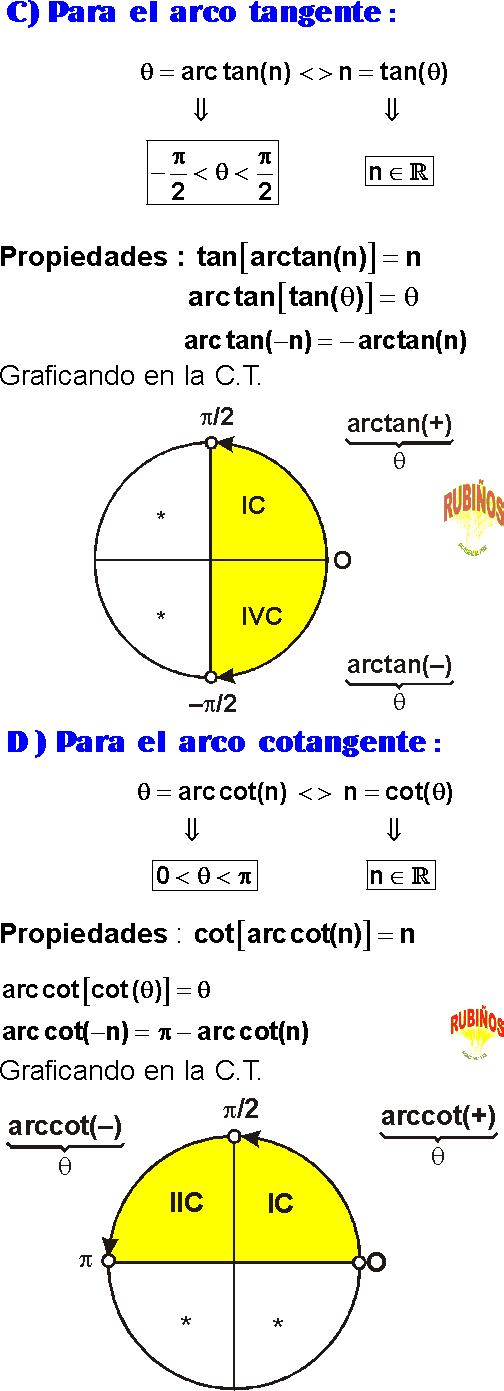
☛ Función arco tangente o tangente inversa
☛ Función arco cotangente o cotangente inversa
☛ Función arco secante o secante inversa
☛ Función arco cosecante o cosecante inversa
APRENDIZAJES ESPERADOS
• Interpretar y operar expresiones del tipo Arcsenx, Arccosx , etc; de manera rápida y concreta.
• Despejar ángulos incógnita cuando una razón trigonométrica de un ángulo se reconoce pero no es notable.
• Definir las funciones trigonométricas inversas.
En el capítulo anterior se estableció que una función asigna a cada elemento del dominio, una y solamente una imagen que desde luego puede ser común a varios o a todos los elementos del dominio.
Si la función tiene además la propiedad de que la imagen es exclusiva o sea que cada imagen en el recorrido lo es de un solo elemento del dominio, se dice entonces que esta función establece una correspondencia biunívoca o biyectiva entre los elementos del dominio y los del recorrido.
Cuando tal es el caso, se puede definir una nueva función, inversa de la función original, cuyo recorrido sea el dominio de la primera. Se dice entonces que cada función es la inversa de la otra.
FUNCIONES TRIGOMÉTRICAS INVERSAS
Como las funciones trigonométricas son periódicas, entonces no son inyectivas por lo tanto no tiene inversa en todo su dominio.
Para que existan las inversas de dicha funciones, se debe restringir el dominio de modo que sean inyectivas.
NOTACIONES PARA EL ARCO
Todo arco o ángulo puede ser expresado en términos del valor de sus razones trigonométricas; así por ejemplo si se tiene que: R.T.(θ)= n, entonces θ es el arco o ángulo cuya R.T. es igual a “n”.
Todo arco o ángulo se puede expresar de seis formas diferentes, todas ellas equivalentes entre sí, esto se debe a que son seis razones trigonométricas del ángulo arco , que se puede calcular
Ahora bien, esto ha sido una interpretación bastante simple, sin restricciones; lo cual no es lo más correcto, pero si lo más adecuado para recién exponer sus aspectos teóricos básicos con la rigurosidad que contiene.
VALORES PRINCIPALES PARA LOS ARCOS
Se denomina así a aquel valor del arco que satisface una determinada igualdad y que está dentro del intervalo donde se define la función trigonométrica inversa correspondiente
Para la solución de los problemas es necesario tener presente algunos valores de ángulos notables
MÉTODO DEL CAMBIO DE VARIABLE
Cuando los valores de las funciones trigonométricas inversas no son conocidos es frecuente hacer un cambio
PRACTICA PROPUESTA
EJERCICIO 1 :
Calcula: tan(arccos1/5)
a) √3
b) 2√6
c)√2
d) √7
e) √5
Rpta. : "B"
EJERCICIO 2 :
Calcula.
Sec²(ArcTg3)+ Csc²(ArcCtg5)
a) 34
b) 36
c) 28
d) 8
e) 24
Rpta. : "B"
EJERCICIO 3 :
Calcula: Tan(2arctan1/3)
a) 1/2
b) 3/2
c) 3/4
d) 3/5
e) 3/7
Rpta. : "C"
EJERCICIO 4 :
Calcula:
Cos(arcsen4/5+arccos12/13)
a) 16/13
b) 16/15
c) 17/14
d) 15/14
e) 13/17
Rpta. : "B"
EJERCICIO 5 :
Calcula:
Tan(arctan3/5+arcsen3/5)
a) 25/13
b) 29/13
c) 27/11
d) 16/15
e) 14/11
Rpta. : "C"
EJERCICIO 6 :
Calcula: Sen(2arctan2/3)
a) 12/11
b) 12/7
c) 12/13
d) 13/11
e) 13/17
Rpta. : "C"
EJERCICIO 7 :
Calcula: Cos(3arccos1/3)
a) 25/26
b) –27/28
c) –23/27
d) 27/29
e) 29/25
Rpta. : "C"
EJERCICIO 8 :
Dada la ecuación:
ArcTg(x+1) – ArcTg(x–1) = ArcTg2
Indica la suma de soluciones:
a) – 2
b) –1
c) 0
d) 2
e) 1
Rpta. : "C"
PROBLEMAS RESUELTOS
PREGUNTA 1 :
Determine si es verdadera (V) o falsa (F) cada una de las proposiciones siguientes:
• El dominio de la función arcoseno es igual al rango de la función seno.
• arcsen(sen𝛑/2)=𝛑/2
• arcos(cos𝛑/2)=𝛑/2
• Las funciones seno y coseno son par e impar, respectivamente.
• El dominio de la función arcotangente es ]–𝛑/2;𝛑/2[
A) VFFVV
B) VVFVF
C) FVFVV
D) VVVFF
E) FFVVV
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 2 :
La regla de correspondencia que representa a la gráfica adjunta, es:
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 3 :
Calcular el rango de la siguiente función:
h(x) =2𝜋+ 5arcsen(4x) + 4arccos(4x)
A) [ 5𝛑/2 ; 7𝛑/2 ]
B) [ 3𝛑/2 ; 5𝛑/2 ]
C) [ 9𝛑/2 ; 11𝛑/2 ]
D) [ 7𝛑/2 ; 9𝛑/2 ]
E) [ 11𝛑/2 ; 13𝛑/2 ]
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 4 :
Indique el valor de veracidad (V) o falsedad (F) de las siguientes proposiciones:
A) FVV
B) FFV
C) VFF
D) VFV
E) VVV
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 5 :
¿Cuál de las siguientes funciones es inyectiva?
A) | arctgx|
B) |arcsenx|
C) |arccscx|
D) |arctgx + arcctgx|
E) |arccosx|
RESOLUCIÓN :
Es inyectiva, uno a uno, si a elementos distintos del conjunto X (dominio) les corresponden elementos distintos en el conjunto Y (codominio) de f. Es decir, cada elemento del conjunto Y tiene a lo sumo una preimagen en X, o, lo que es lo mismo, en el conjunto X no puede haber dos o más elementos que tengan la misma imagen.
De acuerdo a la definición la función que cumple es: |arcsenx|
Rpta. : "B"
