FUNCIONES TRIGONOMÉTRICAS EJERCICIOS RESUELTOS PDF
☛ Función seno
☛ Función coseno
☛ Función tangente
PRACTICA
PREGUNTA 1 :
Determine el dominio de la función f(x)= senx + cos(x–1)
A) ℝ
B) ℝ – {1}
C) ℝ – { –1}
D) ℝ – {0}
Rpta. : "D"
PREGUNTA 2 :
La edad de Edu es el triple de la edad de Pedro. Si la edad de Pedro está determinada por el mínimo valor que toma la función real f definida por f(t) = sec4t + csc4t en años, halle la edad de Edu.
A) 21 años
B) 18 años
C) 24 años
D) 27 años
E) 15 años
Rpta. : "C"
PREGUNTA 3 :
Indique qué valor no pertenece al dominio de la función f definida por
f(x)=sen2x+cos²x+ tanx
A) 0
B) 𝛑/6
C) 𝛑/4
D) 3𝛑/2
Rpta. : "D"
PREGUNTA 4 :
En una ciudad la temperatura del día en grados centígrados está dada por la función T definida por
T(t) = 10( ctg(𝛑t/48) − ctg(𝛑t/24) ) , donde t es el tiempo en horas. Si el registro de la temperatura se inicia desde la medianoche, ¿a qué hora la temperatura será de 10°C?.
A) 10 : 00am
B) 09 : 00am
C) 11: 00am
D) 12 : 00m
E) 08 : 00am
Rpta. : "D"
PREGUNTA 5 :
Determine el rango de la función f definida por f(x) =senx.cosx+3
A) [ –1/2; 1/2]
B) [ 5/2; 7/2]
C) [ –1; 1]
D) [ –1; 2]
Rpta. : "B"
PREGUNTA 6 :
El desplazamiento de una partícula está determinada por la función real f definida por
f(t) = csc²t −2csct + 6 en metros, donde t denota el tiempo en minutos tal que t∈ [𝛑/6;2𝛑/3] .
¿Cuál es la diferencia entre la máxima y mínima distancia que se puede alejar la partícula con respecto al eje horizontal?
A) 1 m
B) 2 m
C) 0,5 m
D) 1,5 m
E) 2,5 m
Rpta. : "A"
PREGUNTA 7 :
Determine el rango de la función f definida por
f(x)=2cos(x+ 30º)cos(x – 30º)
A) [ –1/2; 3/2]
B) [ – 2; 2]
C) [ –1; 1]
D) [ –2; 1/2]
Rpta. : "A"
PREGUNTA 8 :
En una ciudad, la temperatura del día en °C está dada por la función real T definida
T(t) = 3ctg²t + 5, 𝛑≤t ≤5𝛑 , donde t es el tiempo en horas.
Calcule la diferencia entre la máxima y mínima temperatura en °C.
A) 11 °C
B) 7 °C
C) 8°C
D) 10 °C
E) 9 °C
Rpta. : "E"
PREGUNTA 9 :
Señale la secuencia correcta de verdad (V) o falsedad (F) según corresponda.
I. La función f(x)=senx, en el intervalo 〈0;𝛑〉 tiene un máximo valor.
II. La función f(x)=senx es creciente en el intervalo ] 𝛑/2;3𝛑/2[
III. La función f(x)=senx interseca al eje x en 3 puntos en el intervalo [0;2𝛑].
A) VVV
B) VFF
C) FFF
D) VFV
Rpta. : "D"
PREGUNTA 10 :
La fuerza electromotriz (en voltios) aplicada a un circuito eléctrico está dada por la función real
E(t) =110sec²(𝛑t/4) + 2 , donde t denota el tiempo en segundos. Si t∈[1;2〉 , ¿cuál será la mínima fuerza electromotriz aplicada al circuito eléctrico?,
A) 225 voltios
B) 215 voltios
C) 210 voltios
D) 222 voltios
E) 220 voltios
Rpta. : "D"
PREGUNTA 11 :
La función real f definida por
f(t)=10csc(𝛑t/8) describe la oscilación de una pesa en centímetros, donde t denota el tiempo en segundos. Halle el periodo de f.
A) 15
B) 16
C) 14
D) 18
E) 13
Rpta. : "B"
PREGUNTA 12 :
En un laboratorio de biología la función real P definida por
P(t) = 5 + 3sec(𝛑t/24) representa el número de bacterias en miles y t el tiempo en días. Si inicio de la observación, ¿cuál es la población de bacterias al octavo día?.
A) 13 000
B) 9 000
C) 10 000
D) 11 000
E) 12 000
Rpta. : "D"
PREGUNTA 13 :
Si [ c;d] es el rango de la función real f definida por halle c+d .
f(x) = 2csc²2x + 4csc2x + 5
𝛑<x ≤ 5𝛑/12
A) 30
B) 28
C) 32
D) 34
E) 29
Rpta. : "C"
PREGUNTA 14 :
Halle el rango de la función real f definida por
f(x)=(sec3x+csc3x−3)(sec3x+csc3x+3)
A) [ −1, +∞〉
B) [ − 8, +∞〉
C) [ − 9, +∞〉
D) [ 9, +∞〉
E) 〈 − ∞, − 9]
Rpta. : "C"
PROBLEMAS RESUELTOS
PREGUNTA 1
Determina el dominio de la función:
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 2 :
Halle el rango de la función
F(x)=sen²x+2senx+𝛑
A) [𝛑; 𝛑+3]
B) [𝛑−1; 𝛑+3]
C) [𝛑−1; 𝛑+4]
D) [𝛑+1; 𝛑+3]
RESOLUCIÓN :
Agregando y quitando 1 :
F(x)=sen²x+2senx+1+𝛑−1
⇒ F(x)=(senx+1)²+𝛑−1
⇒ −1 ≤ senx ≤ 1
⇒ 0 ≤ senx+1 ≤ 2
⇒ 0 ≤ (senx+1)² ≤ 4
⇒ 𝛑 ≤ (senx+1)²+𝛑 ≤ 4+𝛑
⇒ 𝛑 −1 ≤ (senx+1)²+𝛑−1 ≤ 4+𝛑−1
⇒ 𝛑−1 ≤ F(x) ≤ 𝛑 + 3
Rpta. : "B"
PREGUNTA 3
La gráfica que representa a la función definida por:
h(x) =sen2x·cscx , es:
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 4 :
Hallar la suma del mínimo y máximo valor de la función:
y = sen²x + 2senx + 3 ;∀x∈ℝ
A) 2
B) 4
C) 6
D) 7
E) 8
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 5 :
Determinar el rango de la función:
A) [0 ;4]
B) [–4;0]
C) [0 ;2]
D) [–2;4]
E) [2 ;4]
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 6 :
Dada la función:
0<x ≤ 𝛑. Halle el rango de la función f.
A) ]0; 1]
B) [0; 2]
C) ℝ
D) [–1; 1]
E) [–1; 0]
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 7 :
Sea la función, y=f(x)=tgx
Se sabe que:
Dom∈ [0;a] ∪ [b;𝛑]
Ran ∈ [–√3 ;√3 ].
Hallar: a+b
A) 𝛑/4
B) 𝛑/3
C) 𝛑
D) 2𝛑
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 8 :
Calcular el periodo de la siguiente función real:
h(x) = 5sen6(4x+𝛑/3)
A) 𝛑/3
B) 2𝛑/3
C) 𝛑/4
D) 𝛑/2
E) 𝛑
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 9 :
El proceso rítmico de la respiración consiste en periodos alternantes de inhalación y exhalación. Cada 5 segundos se lleva a cabo un ciclo completo (inhalación y exhalación). Si F(t)=asen(bt) representa el flujo de aire en el tiempo t (en litros por segundo) y si la máxima intensidad de flujo de aire es de 0,6 litros/s , obtenga una fórmula que represente este proceso.
A) F(t)=0,6sen(πt/5)
B) F(t)=6sen(πt/9)
C) F(t)=5sen(πt/3)
D) F(t)=4sen(πt/3)
E) F(t)=0,6sen(2πt/5)
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 10 :
Calcular los puntos donde la función es discontinua:
A) 2n, n∈ℤ
B) 2n+ 1, n∈ℤ
C) 2n, n∈ℤ
D) n, n∈ℤ
E) n/2 ,n∈ℤ
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 11 :
Calcule el periodo mínimo de la función f definida por
f(x) =|cos(x)|+|sen(x)|
A) 𝛑/4
B) 𝛑/2
C) 𝛑
D) 3𝛑/2
E) 2𝛑
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 12 :
Calcular el periodo de la siguiente función real:
h(x)=sen2x + cos3x + cos5x
A) 𝛑
B) 2𝛑
C) 2𝛑/3
D) 2𝛑/5
E) 3𝛑
RESOLUCIÓN :
Rpta. : "B"
☛ Función cotangente
☛ Función secante
☛ Función cosecante
APRENDIZAJES ESPERADOS
• Explicar la idea de función trigonométrica.
• Definir dominio, rango y gráfica de una función trigonométrica de variable real.
• Reconocer las características principales de las funciones trigonométricas ; como su dominio , rango, gráfica , periodo , etc .
• Utilizar las gráficas de las funciones trigonométricas para explicar el comportamiento de ciertos fenómenos de la vida diaria.
¿ QUÉ SON DE LA FUNCIONES TRIGONOMÉTRICAS ?
Las funciones trigonométricas son el conjunto no vacío de pares ordenados (x;y) tal que la primera componente es un valor angular expresado en radianes (número real) y la segunda componente es el valor obtenido mediante una dependencia funcional.
¿ QUÉ ES EL DOMINIO DE UNA FUNCIÓN TRIGONOMÉTRICA?
Es el conjunto que tiene como elementos a los valores de la variable “x”(en radianes); de tal manera que la función exista.
¿ QUÉ ES EL RANGO DE UNA FUNCIÓN TRIGONOMÉTRICA ?
Es el conjunto que tiene como elemento a los valores de la variable “y” tal que y=F.T(x). Los criterios que se tiene para calcular el rango de una función trigonométrica es dependiendo de la forma y tomando en cuenta los criterios de las funciones reales.
FUNCIÓN SENO
El dominio de la función y=senx son todos los números reales.
DETERMINACIÓN DEL PERIODO PRINCIPAL
Sabemos que las funciones trigonométricas son periódicas (sen , cos , sec , csc: 2𝛑 ; tan , cot:𝛑); sin embargo este periodo es susceptible de ser modificado cuando sobre la función se efectúa algún tipo de operación o sobre la variable.
Aquí vamos a dar un criterio de análisis del periodo de una función.
En muchos de nuestros que haceres cotidianos las relaciones entre los elementos de dos conjuntos juega un papel muy importante. Como por ejemplo; un padre relaciona la edad de sus hijos con su peso, un agricultor relaciona su producción con sus ingresos, el desgaste de una máquina con el número de horas trabajadas. Estos ejemplos se pueden representar matemáticamente a través del concepto de función, que al parecer fue introducida por René Descartes (1596 - 1650).
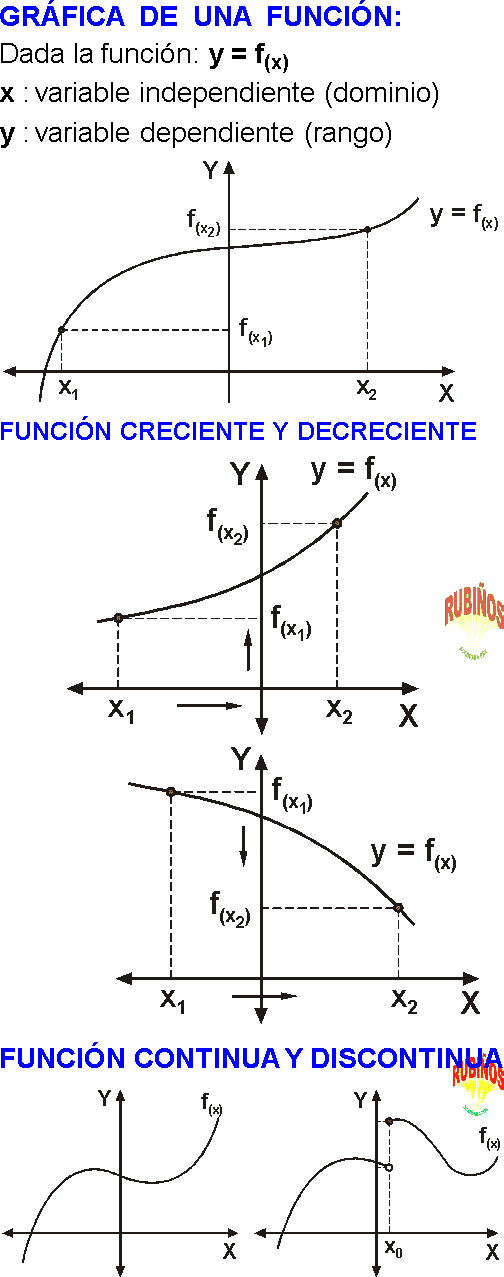
El concepto de función es algo abstracto, sin embargo la representación gráfica de una función (Gráfica de una función), nos muestra con claridad el comportamiento de este tipo de relaciones, en diferentes problemas reales como: la simulación del crecimiento anual de una población, desplazamiento de un móvil en un tiempo dado, reproducción de una bacteria, fenómenos económicos (oferta y demanda, consumo, ingresos) y muchos otros fenómenos como en la medicina, física, electrónica, psicología, etc.
Las funciones reales de variable real son las que dependen de una sola variable (como en el caso de la longitud de la circunferencia que depende solo de su respectivo radio).
La idea de función la entendemos también como la relación que existe entre dos conjuntos, donde a cada elemento de un conjunto le corresponde uno y solo un elemento del otro conjunto. Así por ejemplo, en esta aula , si en un primer conjunto A colocamos a todos sus integrantes y en otro conjunto B colocamos los nombres y apellidos de dichos integrantes, tendremos en consecuencia que a cada elemento del conjunto A le corresponde un solo elemento del conjunto B.
Formalmente una función real de variable real, queda definida por su regla de correspondencia
y = f(x) donde a cada elemento de la variable independiente (x) le corresponde uno y sólo un elemento de la variable dependiente (y).
En el estudio de las funciones trigonométricas directas observamos que su propiedad fundamental es la periodicidad, ya que es un instrumento matemático para describir todos los fenómenos periódicos como los latidos del corazón (mediante el electrocardiograma) y las ondas sonoras.
La mayoría de animales obtienen información del medio ambiente que los rodea detectando algunos tipos de ondas, y se comunican entre sí, produciendo otros tipos de ondas; por ejemplo, el hombre detecta la frecuencia de la luz y el sonido, con los oídos, y la radiación infrarroja con la piel.
