SIMULACRO AGRARIA 2025 RESUELTO INGRESO UNIVERSIDAD PDF

Prueba de ensayo de preparación para afrontar el examen de ingreso a la universidad nacional agraria
RAZONAMIENTO MATEMÁTICO
PREGUNTA 1 : 
Determine el número que sigue en la siguiente sucesión : 
19 ; 20 ; 22 ; 25 ; . . . 
A) 28 
B) 29 
C) 27 
D) 26 
E) 30 
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 2 : 
¿De cuántas formas diferentes se puede ir de A hacia B sin retroceder? 
A) 6 
B) 8 
C) 10 
D) 12 
E) 14 
RESOLUCIÓN :
Rpta. : "B"
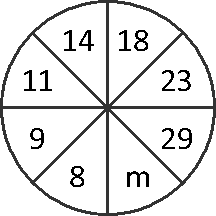
PREGUNTA 3 :
Calcular m en la siguiente figura :
A) 35 
B) 36 
C) 42 
D) 34 
E) 40 
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 4 : 
Halla x+y en la siguiente secuencia :
3 ; 11 ; x; 27; 35 ; y 
A) 62 
B) 52 
C) 42 
D) 82 
E) 32 
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 5 : 
Halla la suma del número de cuadriláteros y el número de triángulos. 
A) 9 
B) 10 
C) 11 
D) 12 
E) 13 
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 6 : 
A) 3 
B) 2 
C) 0 
D) 1 
E) 5 
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 7 : 
Se define una operación matemática en cada caso 
A) 5 
B) 7 
C) 9 
D) 11 
E) 13 
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 8 :
Determinar x en la siguiente distribución :
A) 56 
B) 64 
C) 60 
D) 50 
E) 55 
RESOLUCIÓN :
• (7+2)×3=27 
• (6+4)×5=50 
• (5+3)×7=x=56 
Rpta. : "A"
PREGUNTA 9 : 
En un evento se reúnen 126 profesores; de los que enseñan en la capital, 18 son varones y 12 son mujeres. De cada 24 profesores que son de provincia, 15 son mujeres. ¿En qué relación se encuentra el número de varones y mujeres? 
A) 3: 4 
B) 2: 3 
C) 1: 3 
D) 1: 2 
E) 1: 4 
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 10 : 
Determinar el número total de segmentos que hay en la siguiente figura :
A) 62 
B) 64 
C) 56 
D) 66 
E) 60 
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 11 : 
Un kilogramo de manzanas contiene de 5 a 8 unidades; un kilogramo de naranjas contiene de 4 a 6 unidades. ¿Cuál es el máximo peso que puede tener una decena de manzanas más una decena de naranjas? 
A) 4,0 kg 
B) 4,9 kg 
C) 5,1 kg 
D) 2,4 kg 
E) 5,0 kg 
RESOLUCIÓN :
1 kg de manzanas contiene de 5 a 8 unidades: 
5 manzanas → 1 kg 
12 manzanas → 2,4 kg 
1 kg de naranjas contiene de 4 a 6 unidades: 
4 naranjas → 1 kg 
10 naranjas → 2,5 kg 
Por lo tanto, el peso máximo que puede tener una docena de manzanas más una decena de naranjas es 2,4+2,5 = 4,9kg. 
Rpta. : "B"
PREGUNTA 12 : 
El gráfico muestra las inversiones en cuatro rubros de una cuenta de 50 000 soles. 
Si la suma de las inversiones en los rubros B y C es 8000 soles, ¿cuánto se invirtió en el rubro A? 
A) 25 000 soles 
B) 22 000 soles 
C) 15 000 soles 
D) 20 000 soles 
E) 4000 soles 
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 13 : 
Sobre una mesa, Carlos ordena sus fichas en filas de modo que en la primera fila coloca 7; en la segunda, 13; en la tercera, 24; en la cuarta, 45; y así sucesivamente. ¿Cuántas fichas utilizó Carlos hasta la quinta fila? 
A) 155 
B) 185 
C) 195 
D) 165 
E) 175 
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 14 : 
Calcule el área de la región sombreada. 
A) 6𝛑 m2
B) 8𝛑 m2
C) 10𝛑 m2
D) 18𝛑 m2
E) 28𝛑 m2
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 15 :
Sea: 
A=1+2+3+...+21 
B=2+4+ 6+...+20 
C=1+3+5+...+17 
De como respuesta A+B+C 
A) 420 
B) 520 
C) 422 
D) 522 
E) 622 
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 16 :
Si sabemos que: 
– Jorge es 3 cm más alto que Manuel. 
– Nataly es 2 cm más baja que Manuel. 
– Raúl es 5 cm más bajo que Jorge. 
– Vanessa es 3 cm más baja que Manuel. 
Podemos afirmar que: 
I) Raúl y Nataly son de la misma talla. 
II) Vanessa es la más baja. 
III) Manuel es el más alto. 
A) Todas 
B) I y II 
C) I 
D) II y III 
E) I y III 
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 17 : 
Una compañía de renta de autos cobra $30 al día y $0,15 por kilómetro para rentar un auto. Ernesto renta un auto durante dos días y su cuenta llega a $108. Determine cuántos kilómetros recorrió si se sabe que dicha renta sigue el modelo: 
0,15x+2(30)=108 
(x: Número de km recorridos durante dos días) 
A) 310 
B) 320 
C) 330 
D) 340 
E) 350 
RESOLUCIÓN :
0,15x+60=108 
0,15x=48 
15x/100=48 
15x=4800 
x=320 
∴ Ernesto recorrió 320 km. 
Rpta. : "B"
PREGUNTA 18 :
Manuel tiene el triple de la edad de Sara que tiene 12 años. ¿Cuántos años pasarán para que la edad de Manuel sea el doble de la edad de Sara? 
A) 17 años 
B) 20 años 
C) 25 años 
D) 15 años 
E) 12 años 
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 19 : 
En la figura tenemos el cuadrado ABCD y una semicircunferencia con centro en O y radio 2u. Halla el perímetro de la región sombreada. 
A) 2(6+𝛑)u 
B) 2𝛑+3 u 
C) 2(𝛑+3) u 
D) 2(5+𝛑) u 
E) 3𝛑+4 u 
RESOLUCIÓN :
El perímetro de la región sombreada está conformado por 3 lados del cuadrado y la longitud de la semicircunferencia. 
Rpta. : "A"
PREGUNTA 20 :
En una mesa circular con seis asientos simétricamente colocados, se sientan seis amigos para almorzar. Si Luis no está sentado el lado de César ni de Raúl; Pancho no está al lado de César ni de Mario, Antonio está junto y a la derecha de Pancho. Además, al frente de Antonio no se sienta Mario. ¿Quién está junto y a la derecha de Mario? 
A) Pancho 
B) Raúl 
C) César 
D) Mario 
E) Antonio 
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 21 : 
En una granja dedicada a la crianza de aves se tiene un tanque lleno de agua hasta sus 2/7 partes de su capacidad. Si se añade 516 litros, el nivel del agua sube hasta los 9/10 de su capacidad. ¿Cuántos litros faltan para llenar el tanque? 
A) 84 
B) 204 
C) 304 
D) 104 
E) 94 
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 22 : 
Reina va de compras durante 7 días seguidos, el primer día gasta a soles, el segundo a–6 soles, el tercero a–9 soles y así sucesivamente. Si los gastos diarios están en progresión geométrica, ¿cuánto gastó en los primeros 4 días? 
A) 2,50 soles 
B) 27,50 soles 
C) 20,00 soles 
D) 18,00 soles 
E) 22,50 soles 
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 23 :
Pedro dice: “si hubiera nacido 18 años después, entonces mi edad sería la tercera parte de la edad que tendría si hubiera nacido 8 años antes”. ¿Qué edad tendrá Pedro dentro de 7 años? 
A) 31 
B) 20 
C) 46 
D) 38 
E) 39 
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 24 : 
Pocho repartió billetes de S/ 50, S/ 100, S/ 20 y S/ 10 entre sus cuatro amigas, un billete a cada una. Se sabe que cada una dijo: 
– Carla: “Yo recibí S/ 50”. 
– Andrea: “Yo recibí S/ 100”. 
– Juana: “Carla recibió S/ 10”. 
– Vicky: “Yo recibí S/ 10”. 
Si solo una de ellas miente y las demás dicen la verdad, ¿cuánto suman las cantidades que recibieron Andrea y Vicky? 
A) 120 
B) 110 
C) 70 
D) 30 
E) 150 
RESOLUCIÓN :
Carla: “Yo recibí S/50”    (V) 
Andrea: “Yo recibí S/100”    (V) 
Juana: “Carla recibió S/10”    (F) 
Vicky: “Yo recibí S/10”    (V) 
Se observa que Juana y Vicky se contradicen, por lo tanto una de ellas miente. Además, Carla y Andrea dicen la verdad (V). Luego, como Carla recibe S/50, el enunciado de Juana es falso (F); por lo que Vicky recibí S/10 y Juana S/20. 
Luego: Andrea+Vicky= 100+10= 110 soles 
Rpta. : "B"
PREGUNTA 25 : 
Un insecto se traslada desde el punto B hasta el punto D siguiendo la trayectoria representada por las líneas punteadas. Halla la longitud de dicha trayectoria, si ABCD es un cuadrado y los arcos BO , OD son cuartos de circunferencias. (O es centro del cuadrado). 
A) (2𝛑+3)u 
B) 3𝛑u 
C) 𝛑u 
D) (𝛑+4)u 
E) 2𝛑u 
RESOLUCIÓN :
La longitud de la trayectoria está determinada por la suma de la longitud del cuarto de circunferencia BEO y la longitud del cuarto de circunferencia OFD. 
Rpta. : "E"
ARITMÉTICA
PREGUNTA 1 :
Un granjero tiene 750 huevos. El 4% de estos se rompen y se encuentra que el 5% de los restantes son defectuosos. ¿Cuántos huevos pueden venderse en el mercado? 
A) 300 
B) 450 
C) 675 
D) 684 
E) 692 
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 2 :
Una pelota cae desde cierta altura y en cada rebote pierde 1/3 de la altura de donde cayó. Si cae desde 27m, ¿qué altura alcanza luego del tercer rebote? 
A) 6 m 
B) 8 m 
C) 5 m 
D) 12 m 
E) 16 m
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 3 :
Si la suma de 2 números es M y la diferencia es N. ¿Cuál es la razón geométrica entre el mayor y menor? 
A) (M–N)/(M+N) 
B) (M+N)/(M–N) 
C) (M+N)/2 
D) (M–N) / 2 
E) (M+N)/M
RESOLUCIÓN :
Rpta. : "B"
COMPRENSIÓN DE LECTURA
TEXTO
El sistema beneficiario y el municipal se contraponían en Roma. Mientras el primero beneficiaba a individuos que pertenecían a la nobleza de sangre , el otra a magistrados y ricos. Además , aquel estuvo regido por una autoridad paternalista y al servicio de los aristócratas. Las normas jurídicas establecían el sistema municipal y la tierra era común a todos los munícipes , a su vez la autoridad descansada en la asamblea. Sin embargo , al no poder encontrar una definición exacta para estos sistemas , nos parece llamarlos democráticos. 
PREGUNTA 1 :
Esencialmente el texto pone en contraste : 
A) El estado beneficiario y el aristocrático 
B) Dos formas de autoridades gubernamentales 
C) Las autoridades constituidas por asambleas 
D) El sistema beneficiario y el municipal 
E) El paternalismo en la sociedad romana 
RESOLUCIÓN :
En el texto se señalan una serie de caracteres distintivos tanto del sistema beneficiario como del municipal. Las ideas secundarias que desarrollen dicha idea muestran a los personajes constitutivos de cada sistema así como sus intereses y los órganos en los que descansaba su poder. 
Rpta. : "D"
PREGUNTA 2 :
En el sistema municipal la autoridad descansaba en : 
A) Todos los miembros 
B) Los paternalistas 
C) Los asambleistas 
D) Altos funcionarios 
E) Los de raza noble
RESOLUCIÓN :
En el texto se señala que la autoridad del sistema municipal descansaba en la asamblea. Evidentemente , quienes integraban este órgano supremo eran los asambleistas. 
Rpta. : "C"
PREGUNTA 3 :
Mientras el sistema municipal se establecía por normas jurídicas , en el aristocrático se hacía por: 
A) El sistema beneficiario 
B) Los munícipes 
C) La autoridad paternalista 
D) El sistema democrático 
E) La asamblea 
RESOLUCIÓN :
En el texto se dice: ‘‘aquel (elemento referencial que alude al primer sistema , es decir , el aristocrático) estuvo regido por una autoridad paternalista’’. Esta última expresión es correspondiente con la alternativa C , por transcripción. 
Rpta. : "C"
PREGUNTA 4 :
¿A quién beneficiaba la tierra en el sistema municipal? 
A) A los que la trabajaban. 
B) A poderosos y magistrados. 
C) A los que la heredaban. 
D) A los demócratas. 
E) A todos los individuos. 
RESOLUCIÓN :
La respuesta se remite a una aseveración expuesta por transcripción. 
Rpta. : "B"
PREGUNTA 5 :
En el sistema municipal la aristocracia estaba conformada por: 
A) Dueños de la tierra. 
B) Magistrados y poderosos. 
C) Los protectores con autoridad paternal. 
D) Nobles de aristocracia. 
E) Municipales y aristócratas.
RESOLUCIÓN :
La respuesta se remite a una información expuesta por transcripción. 
Rpta. : "B"
TEXTO II 
Gracias a las jergas, podemos comunicarnos más rápido y nuestra vida ya no se hace tan “lenteja”, “habla al toque, choche, que me veo con Apurímac”. Y es que la jerga dejó de ser comprendida solo como propiedad de grupos marginales para ser abordada como una expresión de todos los estratos sociales y edades, así también invade en distintos ámbitos, como la política. Alguien que ya está “tío” todavía dice que está “carreta”, pero es probable que su nieto le cuente que para enviando “emilios” a través de la red a todos sus “brothers”. Así, es posible seguir con más ejemplos, entonces mejor dejemos el “floro” del lado y pongámonos “seriales”: Óscar Quezada, semiólogo muy conocido en el ámbito académico, establece una génesis de la jerga en los diferentes contextos y refiere lo siguiente: “El medio ambiente, la ecología en la que se mueve la jerga al nacer es la lengua oficial. Su aparición tiene que ver con la permutación, por ejemplo, el paso de la palabra “baño” a “ñoba”. En ese sentido, se parte de la alternación fonológica y/o semántica de un habla establecida. La jerga se reconoce como tal por diferenciarse de la norma, al quebrarla, desarticularla y establecer una forma de expresión particular”. 
PREGUNTA 6 :
¿Cuál sería el mejor título para el texto? 
A) ¿Qué sería de nosotros sin la jerga? 
B) Las jergas de ayer y hoy 
C) Las jeringas en la comunidad 
D) La diferencia entre las jergas y la lengua oficial 
E) La génesis de las jergas por los semiólogos 
RESOLUCIÓN :
El mejor título para el texto es la diferencia entre las jergas y la lengua oficial. El texto explica que las jergas surgen a partir de la alteración fonológica y/o semántica de un habla y se diferencian de la norma de una lengua oficial al desarticularla y establecer una forma particular de expresión.
Rpta. : "D"
PREGUNTA 7 :
Si el individuo no empleara las cargas, entonces 
A) viviría relegado de la sociedad. 
B) el idioma español no se “contaminaría”. 
C) se conservaría la “pureza” del español. 
D) habría más inteligibilidad en la comunicación. 
E) el léxico sería menos numeroso. 
RESOLUCIÓN :
Si el individuo no empleara las jergas, entonces el léxico sería menos numeroso. Esto debido a que en el texto se explica, mediante diversos ejemplos, las nuevas construcciones de palabras a partir de la alteración fonológica y/o semántica de un habla. Entonces, desde un enfoque cuantitativo, las jergas incrementan el léxico de una lengua oficial, y si esas no se emplearan, sería menor el bagaje lexical.
Rpta. : "E"
ELIMINACIÓN DE ORACIONES 
A continuación encontrará , para cada pregunta , cinco oraciones que se refieren a un determinado asunto , numeradas del I al V. Luego de leerlas atentamente , elija la alternativa de respuesta correcta (A, B, C, D o E) que contenga la oración que no es pertinente en el conjunto de oraciones o que repite innecesariamente una idea. 
PREGUNTA 1 :
Elegir la oración que debe eliminarse por ser impertinente. 
I) En el capitalismo surge la separación entre el productor y los medios de producción. 
II) Se desarrolla ampliamente la división social del trabajo. 
III) El capitalismo origina un desarrollo vertiginoso de las ciencias.
IV) Además, el objetivo no es satisfacer necesidades, sino individualidades. 
V) La caza de ganancias es la fuerza motriz. 
A) I 
B) IV 
C) III 
D) II 
E) V 
RESOLUCIÓN :
La oración que se elimina del ejercicio es la III. El tema central del ejercicio es la naturaleza individualista del capitalismo, en tal sentido, se elimina la tercera oración, ya que alude a un tema disociado, esto es, el desarrollo de las ciencias en el capitalismo. 
Rpta. : "C"
PREGUNTA 2  :
Señalar qué oración del texto es eliminable porque patentiza una inclusión evidente. 
(1) El mensaje de la abeja exploradora es comunicado a través de pautas de movimiento, llamadas danza, en las paredes verticales del panal. (2) Dependiendo de la situación de la fuente de alimento con respecto al panal, se dan dos tipos de danza: la danza en círculo y la danza de la cola. (3) Si la fuente se encuentra a una distancia comprendida dentro de 10 metros a la redonda del panal, la abeja ejecuta la danza en círculo. (4) Para distancias que superan los 10 metros, la abeja ejecuta la danza de la cola. (5) En un panal, la abeja exploradora comunica sus mensajes a través de danzas. 
A) 4 
B) 2 
C) 1 
D) 5 
E) 3 
RESOLUCIÓN :
La oración que debe eliminarse por patentizar una inclusión evidente es la 5. El ejercicio versa sobre la comunicación de las abejas a través de la danza. La oración 5 redunda en lo expresado por la oración 1; además, esta posee más información que la oración que se elimina. 
Rpta. : "D"
MATEMÁTICA
PREGUNTA 1 : 
Dos cirios de igual altura pero de diferente calidad se encienden simultáneamente: el primero se consume en 4 h y el segundo en 3 h. ¿Cuántas horas después de haber encendido los cirios la altura del primero es el doble de la del segundo?
A) 2 h 
B) 3 h 
C) 4 h
D) 2,5 h 
E) 2,4 h
Rpta. : "E"
PREGUNTA 2 : 
Dos obreros pueden realizar un trabajo en 15 días. Si uno de ellos se demora 16 días más que el otro cuando trabaja solo, ¿en qué tiempo haría la obra el otro solo?
A) 40 días
B) 35 días         
C) 16 días
D) 24 días
E) 18 días
Rpta. : "D"
PREGUNTA 3 : 
Una persona recibe viáticos por 4 días. El primer día gastó 1/5, el segundo día 1/8 del resto, el tercer día los 5/3 del primer día, el cuarto día el doble del segundo día y aún le quedan S/.150. ¿Cuál fue la cantidad entregada?
A) 150 
B) 900 
C) 850
D) 250 
E) 750
Rpta. : "C"
PREGUNTA 4 : 
Una persona decide ir al hipódromo después de perder la tercera parte de su dinero, la cuarta parte del resto y la quinta parte del nuevo resto. Luego ella decide apostar todo lo que le queda, de modo que logra ganar el doble y se retira con una ganancia de S/.25 000. ¿Con cuánto dinero fue al hipódromo?
A) S/.100 000 
B) S/.105 000 
C) S/.125 000
D) S/.150 000 
E) S/.200 000
Rpta. : "C"
PREGUNTA 5 : 
A y B pueden hacer una obra en 70 días, B y C en 84 días y A y C en 140 días. ¿Qué tiempo empleará A en hacer el trabajo solo?
A) 210 h 
B) 105 h 
C) 80 h
D) 100 h 
E) 95 h
Rpta. : "A"
PREGUNTA 6 : 
En cuánto tiempo se llenaría un estanque si un caño lo llena en 4 horas y otro lo vacía en 6 h; además, la llave del desagüe empieza a funcionar una hora después de abierta la primera.
A) 9 h 
B) 8 h 
C) 11 h
D) 7 h 
E) 10 h
Rpta. : "E"
PREGUNTA 7 : 
Ricardo pesaba 120 kg y después de una dieta pesó 84 kg. ¿Qué porcentaje de su peso bajó?
A) 30
B) 40
C) 50
D) 60
E) 70
PREGUNTA 8 : 
Una persona quiere rifar una calculadora, emitiendo para esto cierto número de boletos. Si vende a S/.2 cada boleto perderá S/.30 y si vende a S/.3 cada boleto ganará S/.70, ¿cuál es el costo de la calculadora?
A) 180
B) 200
C) 230
D) 300
E) 370
Rpta. : "C"
PREGUNTA 9 : 
Si Camilo después de jugar con sus amigos se dio cuenta de que su dinero se vio afectado y mencionó: Me falta para tener 28 soles el doble de lo que me falta para tener 22 soles. ¿Cuánto dinero tiene Camilo?
A) S/.13
B) S/.14
C) S/.15
D) S/.16
E) S/.17
Rpta. : "D"
PREGUNTA 10 : 
Calcule el precio de un rollo de alambre si se sabe que su mitad, sumada con sus 2/3 partes y sus 5/8 cuestan S/.3870. Dé como respuesta la suma de sus cifras.
A) 8
B) 9
C) 10
D) 11
E) 12
Rpta. : "B"
PREGUNTA 11 : 
Si se sabe que 140 excede al doble de un número en tanto como el triple de dicho número excede a su tercera parte, halle los dos tercios de dicho número.
A) 20
B) 21
C) 22
D) 23
E) 24
Rpta. : "A"
PREGUNTA 12 : 
Se emplean 12 hombres durante 5 días trabajando 6 horas diarias para cavar una zanja de 10 m de largo, 4 m de ancho y 4 m de profundidad. ¿Cuántos días necesitarán 9 hombres trabajando 5 horas diarias para cavar una zanja de 15 m de largo, 3 m de ancho y 3 m de profundidad, en un terreno que ofrece doble dificultad que el primero?
A) 11,0
B) 13,5
C) 12,0
D) 8,0
E) 10,5
PREGUNTA 13 : 
Las bases de un trapecio están en la relación de 1 a 4. Halle la relación que existe entre el segmento que une los puntos medios de sus diagonales y la mediana del trapecio.
A) 3/5
B) 2/5
C) 1/4
D) 2/3
E) 5/3
PREGUNTA 14 : 
Se tiene una bolsa con 7 caramelos de limón, 5 caramelos de fresa y 9 caramelos de menta. ¿cuál es el mínimo número de caramelos que se deben extraer al azar para tener la seguridad de haber extraído por lo menos uno de cada sabor?
A) 16
B) 20
C) 18
D) 17
E) 19
PREGUNTA 15 : 
En una sucesión geométrica, se cumple que el producto del primer término con el tercer término es 36. Si el producto del tercer término con el quinto término es 576, halle la suma de cifras del producto del primer término con el quinto término. Considere que la razón es entera positiva.
A) 7
B) 8
C) 9
D) 10
E) 111
PREGUNTA 16 : 
Se sabe lo siguiente.
– Muchos que han escrito libros son marxistas.
– Nadie que escriba un libro es apolítico.
A partir de lo anterior, se concluye que
A) algunos marxistas son políticos.
B) algunos marxistas son de derecha.
C) muchos no marxistas son apolíticos.
D) todo marxista es político.
E) nadie que sea apolítico ha escrito libros.
PREGUNTA 17 : 
Teresa menciona a su comadre Patricia una mujer muy supersticiosa, la cual tiene una deuda en soles en el banco, cuya cantidad es un número impar, que, si la deuda se multiplica por 16, la cantidad de divisores positivos del producto aumenta en 292. La comadre Patricia aprovecha para solicitar a Teresa la cantidad de divisores positivos impares de su deuda. A lo cual responde Teresa diciendo que es igual a: 
A) 81 
B) 76 
C) 73 
D) 66 
PREGUNTA 18 : 
Carla obtuvo por la venta de mascarillas KN95 de igual precio S/3500 en enero, S/4500 en febrero y S/5500 en marzo. Si el precio de cada mascarilla KN95 es una cantidad entera de soles comprendida entre S/4 y S/8, ¿cuántos soles recaudó en abril si vendió 400 mascarillas KN95? 
A) 2000 
B) 1600 
C) 2400 
D) 2800
PREGUNTA 19 : 
Julián le pide a su hijo Mario que halle el MCD del mayor numeral de 39 cifras en base 16 y del mayor numeral de 52 cifras en base 32; y luego que dicho MCD lo convierta a base 4, para finalmente determinar la suma de sus cifras. ¿Cuál es la respuesta correcta obtenida por Mario? 
A) 39 
B) 45 
C) 72 
D) 78 
PREGUNTA 20 : 
Adán le dice a su abuelo paterno Moisés, la suma de nuestras edades es 132 años y el mínimo común múltiplo de estas es 336, además cuando nací mi padre Jesús tenía 19 años. ¿Cuántos años tenía Moisés cuando nació su hijo Jesús? 
A) 17 
B) 20 
C) 15 
D) 19 
PREGUNTA 21 : 
Al calcular el MCD de los números que representan la cantidad de soles que tienen Alfredo y Ramón, mediante el algoritmo de Euclides se obtuvo como cocientes sucesivos: 3, 1, 2 y 2, en ese orden, resultando el MCD un número primo impar. Si la suma de los divisores positivos de la suma de todos los residuos obtenidos es 60, ¿cuántos soles más tiene Alfredo que Ramón? 
A) 57 
B) 63 
C) 28 
D) 47 
PREGUNTA 22 : 
Un comerciante desea empaquetar en cajas cúbicas 1200 unidades de pan de molde y cada pan tiene la forma de un paralelepípedo cuyas dimensiones son 20 cm, 15 cm y 12 cm. ¿Cuántas cajas cúbicas como máximo podrá utilizar, si estas deben estar completamente llenas? 
A) 25 
B) 30 
C) 20 
D) 35 
PREGUNTA 23 : 
Pedro acostumbra a visitar a sus primas María, Jenny y Paola cada 5, 7 y 4 días respectivamente y en forma permanente. Si el 15 de mayo de 2021 visitó a sus tres primas, ¿cuál será la fecha más próxima en la que Pedro visitará nuevamente a las tres en el mismo día? 
A) 2 de octubre 2021 
B) 1 de octubre 2021 
C) 3 de octubre 2021 
D) 4 de octubre 2021
PREGUNTA 24 : 
En una caja de dulces hay 12 caramelos, 14 chupetines y 16 chocolates. ¿Cuál es el menor número de dulces que se debe sacar para tener con seguridad nueve dulces iguales? A)30 
B) 29 
C) 28 
D.) 25 
E) 27
PREGUNTA 25 : 
¿Cuántos números de 5 cifras existen tal que el producto de sus cifras sea igual a 18? 
A) 90 
B) 70 
C) 100 
D) 110 
E) 120 
PREGUNTA 26 : 
Una pareja de esposos y sus cuatro hijas van al cine y encuentran seis asientos vacíos en la misma fila. Si las cuatro hijas siempre quieren sentarse juntas, ¿de cuantas maneras diferentes puede sentarse toda la familia? 
A) 72 
B) 120 
C) 36 
D) 144 
E) 48 
PREGUNTA 27 : 
¿De cuántas maneras diferentes se pueden ubicar siete personas alrededor de una mesa que tiene forma circular, si dos de ellos nunca se sientan juntos? 
A) 720 
B) 600 
C) 540 
D) 480 
E) 5040 
PREGUNTA 28 : 
A una conferencia asistieron 9 argentinos y 5 peruanos. Se desea formar un grupo de trabajo conformado por 7 de estas personas, ¿de cuántas maneras diferentes se puede formar el grupo si deben estar presentes por lo menos 3 peruanos y por lo menos 3 argentinos? 
A) 1640 
B) 1680 
C) 1029 
D) 1025 
E) 1260 
PREGUNTA 29 : 
Un ómnibus viajó de Lima a Ica y recaudó S/. 528 al cobrar los pasajes de los adulto y S/. 108 por los niños. Para cualquier recorrido el pasaje adulto es de S/.8 y S/.4 el de niños. Si cada vez que un adulto bajó subieron dos niños y cada vez que bajó un niño subieron tres adultos y llegaron a Ica 55 adultos y 11 niños, ¿cuántos adultos y niños partieron de Lima respectivamente? 
A) 20; 8 
B) 18; 5 
C) 22; 5 
D) 16; 6 
E) 17;6 
PREGUNTA 30 : 
Seis compañeras del centro Pre se encuentran en una charla vocacional. Determinar, cuantos saludos se intercambian entre todas como mínimo, si dos de ellas están enemistadas y no se saludan? 
A) 6 
B) 30 
C) 14 
D) 15 
E) 13 
PREGUNTA 31 : 
Si la probabilidad de ser hipertenso en una población es de 0,2, la de ser diabético es de 0,05 y la de ser simultáneamente hipertenso y diabético es 0,01, ¿cuál es la probabilidad de ser hipertenso o diabético pero no ambos? 
A) 0,36 
B) 0,15 
C) 0,23 
D) 0,53 
E) 0,42

Ejercicios resueltos de examen de admisión a la Universidad