RAZONAMIENTO MATEMÁTICO AGRARIA PRUEBA UNALM INGRESO UNIVERSIDAD LA MOLINA RESUELTA

PREGUNTA 1

Erica manifiesta, “si al doble de mi edad le quitamos 13 años, se obtiene lo que me falta para cumplir 50 años”. Determina la edad de Erica. 

A) 20 años 

B) 18 años 

C) 19 años 

D) 22 años 

E) 21 años 

Resolución

Sea x la edad de Erica 

Del dato: 2x –13=50 – x 

⇒ 3x=63 

⇒ x=21 

Por lo tanto, la edad de Erica es 21 años.

Rpta. : "E"

PREGUNTA 2

Halla el número que falta: 

A) 41 

B) 45 

C) 31 

D) 39

E) 51 

Resolución

Observamos las siguientes operaciones: 

Rpta. : "A"

PREGUNTA 3

Se mezclan 20 kg de arroz de 6 soles, con 10 kg de arroz de 3 soles. Calcula el precio de la mezcla. 

A) 3 soles 

B) 4 soles 

C) 5,50 soles 

D) 4,50 soles 

E) 5 soles 

Resolución

De los datos, se tiene: 

20 kg de arroz de 6 soles 

→ Precio: 20 ×6= 120 soles 

10 kg de arroz de 3 soles 

→ Precio: 10 ×3= 30 soles 

Entonces, se tiene en total: 

Cantidad total: 30 kg 

Precio total: 150 soles 

Precio por kg de la mezcla: 

Precio total÷Cantidad total 

= 150÷30=5 

Por lo tanto, el precio por kilo de la mezcla es de 5 soles. 

Rpta. : "E"

PREGUNTA 4

En la sucesión siguiente: 4; 8; 15; 30; 37; 74; 81; X; determina el valor de X. 

A) 88 

B) 162 

C) 158 

D) 132 

E) 138 

Resolución

Rpta. : "B"

PREGUNTA 5

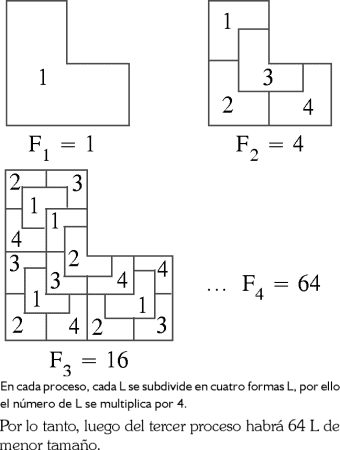
Una figura en L es hecha uniendo tres cuadrados congruentes. La L es subdividida en cuatro formas L como se muestra. Cada uno de los L resultantes es subdividido de la misma forma. Se pregunta cuántas L del menor tamaño existen en la tercera vez que se hace este proceso. 

A) 64 

B) 256 

C) 128 

D) 512 

E) 216 

Resolución

Rpta. : "A"

PREGUNTA 6

Si aαb = a – b + 1, calcule el valor de 

A) a – b 

B) a 

C) b 

D) a + b 

E) 2(a – b) 

Resolución

Rpta. : "A"

PREGUNTA 7

Si la siguiente figura es doblada para formar un cubo, establezca cuál es la figura que se genera. 

Resolución

Rpta. : "A"

PREGUNTA 8

A) 8 

B) 9 

C) 11 

D) 12 

E) 14 

Resolución

Rpta. : "C"

PREGUNTA 9

En el taller mecánico Los Tigres se hace una convocatoria para 2 técnicos especialistas en motores. Se presentaron 5 candidatos y se obtuvieron los siguientes resultados: Luis obtuvo 4 puntos menos que Brayan; Ernesto, 5 menos que Luis; y Justo, 5 más que Piero. Si Piero obtuvo 6 puntos más que Brayan, ¿quiénes fueron contratados? 

A) Piero y Ernesto 

B) Brayan y Piero 

C) Justo y Piero 

D) Justo y Luis 

E) Luis y Piero 

Resolución

Rpta. : "C"

PREGUNTA 10

Sean a, b y c dígitos distintos de cero, tales que 

A) 11 

B) 12 

C) 13 

D) 14 

E) 15 

Resolución

Rpta. : "D"

PREGUNTA 11

Si m*n = 2n² – 3m, calcule el valor de 

A) 6 

B) 5 

C) 4 

D) 3 

E) 2 

Resolución

Rpta. : "D"

PREGUNTA 12

La figura muestra el techo de un edificio, el cual se debe cubrir con material sellador que cuesta S/18 el metro cuadrado. 

¿Cuánto será el costo total del material? 

A) S/1894 

B) S/1796 

C) S/2124 

D) S/1944 

E) S/2016 

Resolución

Área sombreada=10×12 – 4×3

=108 m² 

∴ Costo total =108(18)=S/1944

Rpta. : "D"

PREGUNTA 13

Un triángulo equilátero y un hexágono regular tienen perímetros iguales. Si el triángulo tiene un área de 12 u², ¿qué área tiene el hexágono? 

A) 16 u²

B) 17 u²

C) 12 u² 

D) 18 u² 

E) 19 u²

Resolución

Rpta. : "D"

PREGUNTA 14

Para a y w, números enteros positivos diferentes y menores que 20, tales que a³=w, calcule w². 

A) 64 

B) 81 

C) 100 

D) 76 

E) 49 

Resolución

Rpta. : "A"

PREGUNTA 15

En el sistema de base 8, ¿cuántos números diferentes de cinco cifras pueden escribirse, sin que se repita ninguna y sin que ninguno de ellos tenga la cifra 0? 

A) 2250 

B) 8! 

C) 2520 

D) 21 

E) 720 

Resolución

De acuerdo al enunciado, buscamos los números de 5 cifras diferentes en base 8 que no posean la cifra cero.

Aplicando el principio de multiplicación, se tiene 

Total de números = 7×6×5×4×3=2520 

Por lo tanto, la cantidad de números diferentes es 2520

Rpta. : "C"

PREGUNTA 16

Establezca cuál de las siguientes figuras continúa la sucesión. 

Resolución

Rpta. : "A"

PREGUNTA 17

Calcular el perímetro de la región sombreada si O es el centro del cuadrado ABCD. 

Resolución

Rpta. : "D"

PREGUNTA 18

Un agricultor divide su terreno de forma cuadrada en parcelas como se observa en la siguiente figura: 

Determina cuántos triángulos se puede contar. 

A) 164 

B) 152 

C) 148 

D) 196 

E) 182 

Resolución

Se observa que cada cuadrado de la figura tiene su diagonal y, por lo tanto, se cuenta 2 triángulos; entonces para contar la cantidad de triángulos bastará contar el total de cuadrados y multiplicar por 2. 

Total de cuadrados :

 6² + 5² + 4² + 3² + 2² + 1²= 91 

Total de triángulos = 2(Total de cuadrados)

= 2(91)=182 

Rpta. : "E"

PREGUNTA 19

Qué fracción representa la región sombreada de (I) y (II) respecto a la región no sombreada de (I) y (II). Si la región (II) es el doble de la región (I). 

A) 3/5 

B) 3/4 

C) 2/3 

D) 4/5 

E) 1/3 

Resolución

Rpta. : "D"

PREGUNTA 20

Si la proposición (∼ p ∧ q)→ r≡ F, entonces los valores de verdad de p; q; r, respectivamente, son 

A) FFF 

B) FVF 

C) FVV 

D) VFF 

E) VVF 

Resolución

Del dato, se tiene:

Por lo tanto, los valores de verdad de p, q y r son, respectivamente, FVF

Rpta. : "B"

PREGUNTA 21

Calcule el mayor número de dos dígitos tal que si invertimos los dígitos (decenas en unidades y unidades en decenas) el nuevo número es 75% mayor al número original. 

Indique como respuesta la suma de los dígitos del número. 

A) 10 

B) 12 

C) 9 

D) 6 

E) 3 

Resolución

Rpta. : "B"

PREGUNTA 22

La edad de Pepe está dado por la siguiente suma: P + E + P + E 

Determina dicha edad. 

A) 26 

B) 24 

C) 18 

D) 22 

E) 20 

Resolución

Rpta. : "E"

PREGUNTA 23

Sea el operador * definido en la tabla 

Calcule (x^–1* y^–1) * z, conociendo que b^–1 = a 

A) b * c 

B) a 

C) c * a 

D) a * c 

E) y

Resolución

Sea e: elemento neutro de la operación matemática 

→ b * b^–1=e 

Del dato: b^–1=a, tenemos: 

b * a=e 

→ y=e 

Entonces a^–1=b ; b^–1=a ; c^–1= c (elemento neutro) 

Como c es elemento neutro, se deduce que:

z =a; x=b; y= c 

Reemplazamos en lo que nos piden: 

(x^–1 * y^–1) * z = (b^–1) * c^–1) * a 

= (a * c) * a

=a * a

=x

=b 

Damos forma según las alternativas: 

∴ (x^–1* y^–1) * z =b * c

Rpta. : "A"

PREGUNTA 24

De 7 números positivos y 6 números negativos, se escogen al azar tres números y se multiplican. Calcular el número de combinaciones en que se pueden multiplicar, de tal forma que el resultado sea un número negativo. 

A) 161 

B) 181 

C) 190 

D) 172 

E) 146 

Resolución

Rpta. : "E"

PREGUNTA 25

Luego de interrogar a cinco sospechosos de un crimen, se concluye que hay cuatro culpables y un inocente, quién es el único que dice la verdad. Se sabe que los sospechosos declararon lo siguiente: 

• Samuel : Yo no fui

• Pablo: Samuel miente 

• Jorge: Pablo miente 

• Roberto: Pablo fue 

• Cesar: Roberto dice la verdad 

¿Cuál es el nombre del inocente? 

A) Samuel 

B) Pablo 

C) Jorge 

D) Roberto 

E) Cesar

Resolución

Rpta. : "B"