SOLUCIONARIO EXAMEN SAN MARCOS ÁREA C 2022 II INGENIERÍAS PRUEBA DESARROLLADA DE ADMISIÓN A LA UNIVERSIDAD 2022-2 CLAVES RESPUESTAS SOLUCIONES PDF

HABILIDAD LÓGICO MATEMÁTICA

PREGUNTA 16 :

Un grifo tiene un tanque que contiene gasolina hasta los 4/11 de su capacidad. Cuando llega un camión surtidor y agrega 340 galones de gasolina, la cantidad de gasolina que ahora contiene el tanque alcanza el 75 % de su capacidad. A partir de ese instante, se vende la totalidad de gasolina que tiene el tanque a razón de 20 soles el galón. ¿Cuál fue el ingreso que se obtuvo?

A) S/.12 560

B) S/.13 120

C) S/.13 200

D) S/.10 290

PREGUNTA 17 :

En la tabla se muestra algunos resultados de la final de un torneo disputado por los equipos Alpe, Bizo y Flash, jugando todos contra todos en una sola ronda. Por partido ganado se asignó· 3 puntos al ganador; por partido empatado, 1 punto para cada equipo y por partido perdido, 0 puntos. Además, los goles a favor de cada equipo coincidieron con sus respectivos puntajes. Si ningún partido tuvo el marcador final 1–1, y la diferencia de goles en el partido Flash vs Bizo es 1, ¿cuántos goles en contra tuvo Bizo en el torneo?

A) 5

B) 2

C) 7

D) 4

PREGUNTA 18 :

Las tres balanzas de la figura están en equilibrio. Si los objetos idénticos tienen el mismo peso, ¿cuántos objetos hexagonales pesan lo mismo que un objeto cuadrado?

A) 1

B) 4

C) 3

D) 2

PREGUNTA 19 :

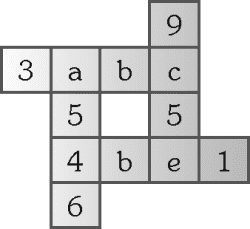
En el arreglo numérico que se muestra en la figura, se cumple que, al sumar los números de · las filas o columnas formadas por cuatro casillas, se obtiene siempre el mismo resultado. Halle el valor de b ÷ c

A) 7

B) 6

C) 5

D) 4

PREGUNTA 20 :

Ofelia tiene un balde lleno de 10 litros de emoliente y dos jarras vacías, una de 7 litros y otra de 5 litros de capacidad. El balde y las dos jarras no tienen marcas que permitan hacer mediciones. Usando solo el balde y las dos jarras y sin desperdiciar emoliente en ningún momento, ¿cuántos trasvases, como mínimo, debe realizar Ofelia para obtener cuatro litros de emoliente en la jarra de siete litros?

A) 5

B) 7

C) 6

D) 8

PREGUNTA 21 :

Dado el siguiente arreglo, considerando igual distancia mínima de una letra a otra en cada lectura, indique de cuántas maneras diferentes se puede leer la palabra CASA.

A) 14

B) 16

C) 8

D) 10

PREGUNTA 22 :

El reloj de mi hermano Aldo se atrasa un minuto cada hora, y el de mi hermana Matilde se adelanta un minuto cada dos horas. Al salir de casa, sincronicé ambos relojes a la misma hora y les dije a mis hermanos que volvería cuando la diferencia de tiempo que marcan sus relojes sea exactamente 30 minutos. ¿Cuántas horas estaré fuera de casa?

A) 40

B) 10

C) 12

D) 20

PREGUNTA 23 :

En la siguiente secuencia de figuras, determine la figura 63.

PREGUNTA 24 :

Manuel, quien entrega pedidos a domicilio, realiza el siguiente recorrido desde su tienda: primero recorre 600 m en dirección N30ºE, hasta la casa de Alex; luego recorre 1200√3 m, en dirección S60°E, hasta la casa de Belén; y finalmente recorre 1800 m en dirección oeste, hasta la casa de Carlos. ¿Qué dirección debe tomar Manuel, desde la casa de Carlos, para retornar a la tienda realizando un recorrido mínimo?

A) N30ºO

B) N60°O

C) NO

D) N37ºO

PREGUNTA 25 :

La siguiente figura representa una estructura tridimensional de alambre. ¿De cuántas maneras distintas se puede ir desde el punto A hasta el punto B, en la estructura, transitando solo por las direcciones indicadas?

A) 64

B) 56

C) 60

D) 68

PREGUNTA 26 :

Un arquitecto está diseñando el plano de un edificio delimitado por el polígono ABCD, como se muestra en la figura. Debido a que en la zona se proyecta construir un centro comercial, al plano del edificio se le deben realizar dos simetrías consecutivas. La primera simetría se realiza tomando como eje de simetría al eje Y, y la segunda simetría se realiza tomando como eje de simetría al eje X. Halle la suma de las ordenadas de las coordenadas de los vértices que resultan de aplicar las dos simetrías a los puntos A, B, C y D.

A) –18

B) –10

C) –16

D) –21

PREGUNTA 27 :

Bill Gates nació el 28 de octubre de 1955 en Seattle (Washington). El 4 de abril de 1975 creó la empresa Microsoft Corporation. ¿Qué día de la semana su empresa cumplirá 100 años de creación?

A) Lunes

B) Martes

C) Sábado

D) Jueves

PREGUNTA 28 :

Manuel tiene una caja no transparente que contiene 27 bolos de igual forma y tamaño , 10 de estos están numerados con el numero 10; 8 están numerados con el número 20 y 9 están numerados con el número 50. ¿Cuántos bolos, como mínimo, debe extraer al azar Manuel, para tener con certeza 3 bolos cuya suma de sus números sea igual a 80?

A) 19

B) 20

C) 18

D) 21

PREGUNTA 29 :

Ocho amigos, cuatro hombres y cuatro mujeres, se sientan en ocho sillas colocadas alrededor de una mesa circular, como muestra la figura.

Se sabe lo siguiente:

► Felipe y Gladys se sientan juntos.

► Belén no se sienta junto a Daniel.

► Daniel se sienta junto y a la izquierda de Ana.

► Carlos no se sienta junto a Ana ni junto a Gladys.

► Héctor llegó un poco retrasado a la reunión.

► Ana está sentada a la izquierda de Luisa.

► Amigos del mismo sexo no se sientan juntos.

¿ Quién está sentada junto y a la izquierda de Héctor?

A) Ana

B) Gladys

C) Luisa

D) Belén

PREGUNTA 30 :

Se tiene las vistas horizontal, frontal y perfil derecho, de un poliedro de volumen máximo, como se muestra en la figura. ¿ Cuántas caras tiene dicho poliedro?

A) 9

B) 7

C) 10

D) 8

CLAVES DE RM : 16)C 17)B 18)C 19)A 20)C 21)A 22)D 23)B 24)A 25)B 26)C 27)D 28)B 29)A 30)C

CLIC AQUÍ Ver LO DE HABILIDAD LÓGICO MATEMÁTICA SOLUCIONES

ARITMÉTICA

PREGUNTA 31 :

Mariela crea una cuenta en Tik Tok el primer día de marzo. Al finalizar el día, ya cuenta con 2 seguidores, el segundo día, 3; tercer día, 14; cuarto día, 11, quinto día, 34; sexto día, 27; séptimo día, 62; octavo día, 51 y así sucesivamente. Determine la suma de cifras de la cantidad total de seguidores que Mariela tuvo el 31 de marzo.

A) 11

B) 5

C) 7

D) 15

PREGUNTA 32 :

Una juguetería que inicia sus ventas a las 08:00 horas con

juguetes por vender, el cambio del personal de cobranza de ese día se hizo a las ________ horas.

A) 13:00

B) 14:00

C) 16:00

D) 15:00

PREGUNTA 33 :

Doce obreros se comprometen a terminar una obra en 21 días. Después de haber trabajado 11 días, cinco obreros dejan el trabajo y solo después de 5 días se decide contratar más obreros con el doble de eficiencia que los anteriores para terminar la obra en la fecha señalada. ¿Cuántos obreros se contrató?

A) 5

B) 10

C) 6

D) 8

PREGUNTA 34 :

La probabilidad de que Raúl escuche la alerta de sismo es de 0,80; si la escucha, la probabilidad de que salga de su habitación a tiempo es de 0,90; y si no la escucha, la probabilidad disminuye a 0,50. Si Raúl llegó a salir a tiempo de su habitación, determine la probabilidad de que él haya escuchado la alarma del temblor.

A) 32/41

B) 36/41

C) 23/82

D) 35/82

CLIC AQUÍ Ver LO DE ARITMÉTICA SOLUCIONES

GEOMETRÍA

PREGUNTA 35 :

Se tiene un tablero de madera de forma triangular ABC; las longitudes de los lados AB; BC y AC son 24 cm, 21 cm y 36 cm respectivamente. A partir de estos datos, un carpintero desea obtener otros dos tableros, también de forma triangular. Para ello, se hará un corte a lo largo de siendo M un punto de AC, de tal forma que m∠ACB=m ∠ABM. Halle el menor perímetro de los tableros resultantes.

A) 54 cm

B) 55 cm

C) 48 cm

D) 51 cm

PREGUNTA 36 :

En una caja de cartón con tapa en forma e cubo, se introduce una esfera. Al cerrar la caja la superficie de cada cara del cubo intersecta en un único puto a la superficie esférica. Si la distancia entre dos caras opuestas del cubo es 6 dm, calcule el volumen de la esfera.

A) 32𝛑 dm³

B) 24𝛑 dm³

C) 36𝛑 dm³

D) 28𝛑 dm³

PREGUNTA 37 :

Con el objetivo de mejorar el orden y la limpieza de las calles, la municipalidad de un distrito ha optado por colocar tachos de basura en forma de un tronco de cilindro circular recto, tal como se muestra en la figura. Si la tapa del tacho tiene un diámetro de 60 cm y el área de la superficie lateral del tacho es 7200𝛑 cm², halle el volumen de dicho tacho.

A) 216000𝛑 cm³

B) 14000𝛑 cm³

C) 120000𝛑 cm³

D) 108000𝛑 cm³

PREGUNTA 38 :

En el interior de una copa que tiene la forma de un cono circular recto invertido, se introduce una esfera como se muestra en la figura. Si AB es diámetro y tangente en el punto T a la esfera y m∠CAB=60°, halle la relación entre las áreas de la superficie esférica y la superficie interior cónica.

A) 1/3

B) 2/3

C) 1/2

D) 3/4

CLIC AQUÍ Ver LO DE GEOMETRÍA SOLUCIONES

ÁLGEBRA

PREGUNTA 39 :

El área de una región cuadrada es

; sus cifras son las raíces del polinomio

P(x)=x³ – (n+3)x² + (5n+6)x – 8n

Calcule el volumen de la caja cuyas longitudes de largo, ancho y altura son (a+b) m, (a – 2) m y (b – 3) m respectivamente.

A) 260 m³

B) 250 m³

C) 290 m³

D) 280 m³

PREGUNTA 40 :

Un comerciante va al mercado mayorista con 3040 soles para abastecer su almacén con sacos de arroz y azúcar. El comerciante debe comprar, por lo menos, 15 y, a lo más 30 sacos de arroz; por lo menos 10 y a lo más 20 sacos de azúcar; y entre ambos productos, debe comprar, por lo menos, 32 sacos. Si cada saco de arroz y azúcar cuesta 90 y 100 soles, respectivamente, determine cuántos soles, como máximo, le quedarán al comerciante después de haber hecho sus compras.

A) 30

B) 40

C) 60

D) 10

PREGUNTA 41 :

Los datos para calcular la temperatura de cierta ciudad del norte del país fueron extraviados y solo se sabe que a las t horas está modelada en grados centígrados por la función T, cuya regla de correspondencia está definida por

T(t)=a|t – b|+c ; 0 ≤ t ≤ 24

Si se sabe que la temperatura a las 0, 12 y 24 horas del día es de 14 ; 34 y 24 grados centígrados respectivamente, y 12<b<24, determine la suma de los valores máximos y mínimo que toma la función.

A) 53

B) 39

C) 47

D) 49

PREGUNTA 42 :

La deformación de un objeto debido a la temperatura está modelada por la función f, definida por

f(x)=| 2x² – a|x|+b |; a>b, donde x está dada en grados Celsius.

Si f (– 4)=6 y f (2)=2, halle la suma del mayor valor positivo con el mayor valor negativo, para los cuales la gráfica de la función dada corta el eje de las abscisas.

A) 4

B) 2

C) 6

D) 8

CLIC AQUÍ Ver LO DE ÁLGEBRA SOLUCIONES

TRIGONOMETRÍA

PREGUNTA 43 :

Dos sonidos son representados y graficados en una pantalla, mediante un osciloscopio, por la función

de todos los valores de t ∈ [0,2] para que las funciones F y G tomen el mismo valor.

A) 11

B) 6

C) 13/2

D) 35/4

PREGUNTA 44 :

Dos veleros están ubicados en los puntos A y B respectivamente. Además, la vela ubicada en A se encuentra a 156 metros de un muelle ubicado en el punto C, tal como se muestra en la figura. Si se sabe que α y β son ángulos agudos, tal que senα =24/25 y senβ=416/425 , determine la distancia que separa los veleros.

A) 75 m

B) 80 m

C) 70 m

D) 153 m

PREGUNTA 45 :

En una ciudad, si la temperatura diaria, x horas después de las 8:00 a.m., está representada por

determine a qué hora del día la temperatura es mínima.

A) 12:00 m.

B) 2:00 p.m.

C) 3:00 p. m.

D) 1:00 p.m.

CLIC AQUÍ Ver LO DE TRIGONOMETRÍA SOLUCIONES

CLAVES DE MATEMÁTICA: 31)B 32)D 33)A 34)B 35)A 36)C 37)D 38)B 39)D 40)C 41)A 42)B 43)C 44)A 45)D

LENGUAJE

PREGUNTA 46 :

De acuerdo con la normativa ortográfica vigente establecida por la RAE, marque la alternativa que presenta empleo adecuado de este tipo de letras.

A) Mi amiga Juana me regaló un lindo gato Persa .

B) Ayer se festejó el Día Internacional de la Mujer.

C) La selección peruana de fútbol visitó El Vaticano.

D) El Presidente dialogó con el Ministro de Economía.

PREGUNTA 47 :

La frase nominal tiene por núcleo el nombre o pronombre; de acuerdo con las clases de modificadores que lo acompañan, ella puede clasificarse en compleja o incompleja. Conforme a esta premisa, identifique la alternativa que presenta una frase nominal incompleja.

A) Alberto, el nuevo joyero, regresó temprano.

B) El perro de los Ramírez ha ladrado sin cesar.

C) La señora que quería cantar se retiró molesta.

D) La niña pecosa viajaba frecuentemente sola.

PREGUNTA 48 :

La preposición es una categoría lexical invariable que funciona como nexo subordinante; su significado es contextual. De acuerdo con lo afirmado, cuantifique las preposiciones del enunciado «En plena fiesta, la esposa de Pedro adornó la torta con unas velas amarillas sobre la fresa gigante».

A) Cuatro

B) Cinco

C) Tres

D) Siete

PREGUNTA 49 :

Sintácticamente, las palabras o frases pueden cumplir diversas funciones en una oración: sujeto, objeto directo, objeto indirecto, atributo, etc. En el enunciado «Pedro recibió, nervioso, la medalla de oro en una grandiosa ceremonia de promoción», los elementos subrayados funcionan, respectivamente, como

A) sujeto y objeto indirecto.

B) predicativo y objeto directo.

C) vocativo y atributo.

D) atributo y predicativo.

PREGUNTA 50 :

Según las normas de la RAE, solo algunas palabras se escriben con tilde. De acuerdo con ello, identifique el enunciado correctamente escrito.

A) ¿Es aquí dónde está escondido mi sobrino?

B) Está en algun lugar de aquel recóndito país.

C) Honestamente, nunca dejé de pensar en ti.

D) Se percató de que en el patio no habia nadie.

PREGUNTA 51 :

Nos entendemos y nos definimos como seres humanos por el lenguaje. A continuación, señale la alternativa correcta respecto de las características del lenguaje.

I. Es universal porque es propio de la especie humana.

II. Es social porque relaciona a todas las personas.

III. Es mutable porque las lenguas cambian con el tiempo.

IV. Permite aprender cualquier lengua según el contexto.

A) Solo I

B) I, III

C) I, IV

D) Solo III

PREGUNTA 52 :

Las unidades léxicas se relacionan unas con otras tanto por su forma como por su significado. Tomando en cuenta esta afirmación, identifique, a partir del siguiente texto, la relación correcta entre los elementos.

Ernesto ha construido infraestructuras como el aeropuerto, con su singular torre de control, y el puente San lgor. El concejo optó por votar a favor de su continuidad en las labores y de que sea él quien construya el velódromo de la ciudad. «No es justo botar a un profesional altamente calificado», opinó un ciudadano.

I. Hiperonimia

II. Cohiponimia

III. Homonimia

IV. Meronimia

a. Aeropuerto - puente

b. Torre - aeropuerto

c. Votar - botar

d. Infraestructura - aeropuerto

A) la, IId, IIIc, IVb

B) Id, IIb, IIIa, IVc

C) lc, IId, IIIa, IVb

D) Id, IIa, IIIc, IVb

CLAVES DE LENGUAJE: 46)B 47)D 48)A 49)B 50)C 51)C 52)D

CLIC AQUÍ Ver LO DE LENGUAJE SOLUCIONES

LITERATURA

PREGUNTA 53 :

Edgardo Rivera Martínez es un escritor que combina creativamente lo andino y lo hispano en su obra narrativa. Ha publicado el cuento «Ángel de Ocongate», que desarrolla un extenso monólogo de carácter acerca ____________ de ______________________

A) circular - la identidad individual y cultural de un personaje sincrético

B) delirante - un orate que deambula extraviado por la inhóspita puna

C) religioso - un danzak solitario y sin familia en la sierra sur peruana

D) cultural - la naturaleza andina y la soledad de sus paisajes altiplánicos

PREGUNTA 54 :

Cual suele el ruiseñor con triste canto

quejarse, entre las hojas escondido,

del duro labrador, que cautamente

le despojó su caro y dulce nido

de los tiernos hijuelos, entre tanto

que del amado ramo estaba ausente,

y aquel dolor que siente

con diferencia tanta

por la dulce garganta

despide, y a su canto el aire suena,

y la callada noche no refrena

su lamentable oficio y sus querellas,

trayendo de su pena

al cielo por testigo y las estrellas.

En el poema «Égloga I», del escritor español Garcilaso de la Vega, sus versos tratan

A) del destino del hombre ante la adversidad.

B) del lamento ante la pérdida de lo amado.

C) de la soledad del hombre en la modernidad.

D) de la intensificación del sufrimiento del ser.

PREGUNTA 55 :

«- ¿Había salido a dar un paseo?

– Sí -susurró Sonia, confusa otra vez y con la mirada gacha.

– Según tengo entendido, Katerina lvánova la trataba de mala manera, casi a golpes. Sonia le miró casi asustada:

– ¡Qué va! ¿Qué dice usted? ¡En absoluto!

– De manera que la quiere usted, ¿no?

– ¿Qué si la quiero? ¡ Pues claro! - contestó Sonia con voz lastimera y juntando devotamente las manos-, ¡Ay, pero si usted ... si usted la conociera! Es igual que una criatura ... Parece enteramente como si hubiera perdido el juicio del dolor. ¡Tan inteligente como era, tan generosa ... tan buena! Usted no sabe ... no se puede imaginar ... ¡Ay!». ·

En el pasaje citado de la novela Crimen y castigo, del escritor ruso Fiódor Dostoievski, el personaje Sonia se caracteriza por

A) encarnar humildemente el símbolo de la práctica cristiana.

B) cumplir el rol de una sirvienta muy leal, sumisa y laboriosa.

C) ser cómplice en los crímenes que perpetraba Raskólnikov.

D) mostrar nobles sentimientos hacia quien la habría maltratado.

PREGUNTA 56 :

Entre los autores de la Generación del 50, Blanca Varela destaca por una poesía intelectual y sensorial. Su libro más relevante es Canto Villano, que constituye una experiencia cultural múltiple porque

A) usa imágenes de un surrealismo ortodoxo basado en la escritura automática.

B) emplea algunas letras de valses criollos para parodiarlas y resignificarlas.

C) recupera nostálgicamente la cosmovisión costeña criolla y tradiciones populares.

D) elije sobre todo temas asociados con la maternidad, la familia y lo femenino.

CLAVES DE LITERATURA: 53)A 54)B 55)D 56)D

CLIC AQUÍ Ver LO DE LITERATURA SOLUCIONES

PSICOLOGÍA

PREGUNTA 57 :

La teoría triangular del amor, de R. Sternberg. sostiene que el amor está compuesto por tres dimensiones que se manifiestan en cualquier relación amorosa. Identifique la alternativa que relaciona correctamente cada concepto con sus respectivas características.

I. Intimidad

II. Compromiso

III. Pasión

a. Necesidad de estar con la otra persona, y tener relaciones íntimas

b. Conexión estrecha de confianza, amistad y afecto hacia otra

c. Mantener la relación con esa persona con la que se comparte los buenos y malos momentos

A) Ia, IIb, IIIc

B) Ic, IIb, IIIa

C) Ia, IIc, IIIb

D) Ib, IIc, IIIa

PREGUNTA 58 :

Arturo, estudiante universitario, dice: «Me he matriculado en este curso con mucho interés, pero al revisar las lecturas respectivas, me he dado cuenta de que no logro entenderlas plenamente porque no conozco fa terminología. Por eso he decidido revisar un diccionario de la especialidad y, una vez conocidas las acepciones, las contextualizaré según las lecturas, para comprenderlas y posteriormente repasarlas». En este caso, Arturo está aplicando estrategias de aprendizaje

A) de ensayo.

B) afectivas.

C) metacognitivas.

D) de organización.

PREGUNTA 59 :

Cuando a Alonso, un niño de un año de edad, le dicen «despídete de tu papá», mueve su mano reproduciendo un gesto de adiós, pero sin articular palabra alguna. Esto revela que

I. la comprensión del lenguaje es anterior a la producción del lenguaje.

II. los componentes del lenguaje no se desarrollan de una manera uniforme.

III. a esa edad no hay expresión oral porque aún no se puede imitar palabras.

IV. el desarrollo del lenguaje es mucho más lento en los niños que en las niñas.

A) III y IV

B) I y II

C) I y III

D) II y IV

PREGUNTA 60 :

A sus 22 años, Enrique se ha graduado de ingeniero con altas calificaciones, pero no se siente feliz porque esa carrera la eligió su padre: él quería estudiar cine. Aun no consigue trabajo, por lo que se siente frustrado; desea disponer de su propio dinero para independizarse del hogar paterno y financiar la carrera que desea. Está pensando postular a una beca de estudios en el extranjero, pero viene postergando esta decisión porque evita enfrentarse a su padre. Según la teoría de Deci y Ryan, Enrique tiene insatisfecha la necesidad psicológica de

A) autorregulación.

B) autoeficacia.

C) autoestima.

D) autonomía.

CLAVES DE PSICOLOGÍA: 57)D 58)C 59)B 60)D

CLIC AQUÍ Ver LO DE PSICOLOGÍA SOLUCIONES

EDUCACIÓN CÍVICA

PREGUNTA 61 :

Guarido se hace alusión al mecanismo estatal encargado de articular esfuerzos, coordinar acciones y proponer políticas de corto, mediano y largo plazo dirigidas a prevenir y combatir la corrupción en el país, nos estamos refiriendo

A) a la Comisión de Alto Nivel Anticorrupción.

B) a la Comisión Nacional Anticorrupción.

C) al Sistema Nacional Anticorrupción.

D) a la Oficina de Transparencia y Anticorrupción.

PREGUNTA 62 :

La Constitución Política del Perú establece que todo peruano tiene derecho a usar su propio idioma ante cualquier autoridad mediante un intérprete y que los extranjeros tienen este mismo derecho cuando son citados por cualquier autoridad. Dado el caso, se les estaría garantizando principalmente el derecho a la

A) libertad de expresión.

B) identidad cultural.

C) diferencia cultural.

D) identidad psicológica.

PREGUNTA 63 :

El derecho de los ciudadanos a manifestar sus intereses y demandas a través de actos orientados a influir en la formulación y toma de decisiones gubernamentales con el fin de contribuir a mejorar la gestión pública y la calidad de vida de los ciudadanos es reconocido de la Constitución y se denomina

A) participación ciudadana.

B) consulta previa.

C) participación deliberativa.

D) control ciudadano.

PREGUNTA 64 :

Robles ha considerado que el concepto derechos humanos o derechos del hombre, llamados clásicamente derechos naturales y, en la actualidad, derechos morales, no son en realidad auténticos derechos -protegidos mediante acción procesal ante un juez- sino criterios morales de especial relevancia para la convivencia humana y que, en todo caso, «una vez que los derechos humanos, o mejor dicho, determinados derechos humanos, se positivizan, adquieren la categoría de verdaderos derechos protegidos procesalmente y pasan a ser derechos fundamentales, en un determinado ordenamiento jurídico».

Adaptado de Aguilar, G. (2010). Derechos fundamentales-derechos humanos. ¿Una distinción válida en el siglo XXI?

De acuerdo con el pasaje citado, ¿qué alternativa es verdadera?

I. La noción de derechos naturales carece de eficacia jurídica y ha quedado obsoleta.

II. El concepto de derechos fundamentales protege jurídicamente a las personas.

III. La categoría de derechos humanos debe ser abandonada por su ineficacia jurídica.

A) Solo I y III

B) Solo I y II

C) Solo II y III

D) I,II y III

CLAVES DE CÍVICA: 61)C 62)C 63)B 64)C

CLIC AQUÍ Ver LO DE CÍVICA SOLUCIONES

HISTORIA DEL PERÚ

PREGUNTA 65 :

Terminada la guerra contra Chile, la población andina de la sierra norte inició una insurrección al saber que el alcalde del pueblo de Marian, del departamento de Ancash, había recibido como respuesta el encarcelamiento por elevar un memorial a las autoridades de la capital. Esta medida generó un descontento incontrolable en la población indígena al enterarse que se había decretado

A) el incremento del precio de los alimentos.

B) el restablecimiento del tributo indígena.

C) la prohibición de los cultivos y venta de coca.

D) la reducción de las tierras de su comunidad.

PREGUNTA 66 :

Con los acontecimientos en las salitreras de Antofagasta, se inicia una etapa trágica para la historia del Perú que condujo a la guerra contra Chile. Las crisis de toda naturaleza y sus impactos siempre han sido motivo y justificación para concretar decisiones de intereses ocultos de Estado para tomar una iniciativa bélica. En estas circunstancias,

B) Chile promovió la misión José Antonio de Lavalle.

B) Juan de la Cruz Benavente negocia la alianza secreta con Argentina.

C) José de la Riva-Agüero firma la alianza defensiva con Bolivia.

D) La declaratoria de guerra de Chile al Perú se publicó en La Abeja Republicana.

PREGUNTA 67 :

Transcurría un año desde que estalló en los Estados Unidos de Norteamérica la primera gran crisis del capitalismo de comienzos del siglo XX (1929), mientras en el Perú,

A) el presidente Augusto Leguía cerraba el congreso.

B) se iniciaba una revuelta popular en Trujillo.

C) se inauguraba en Lima la plaza San Martín.

D) el gobierno de Luis Sánchez Cerro se consolidaba.

HISTORIA UNIVERSAL

PREGUNTA 68 :

La revolución de 1848 fue un amplio movimiento político que abarcó gran parte de Europa. Tuvo reivindicaciones sociales y políticas que buscaban consolidar los ideales planteados por la Revolución francesa, así como democratizar sus respectivas sociedades. Dos de esas reivindicaciones fueron

A) el reconocimiento legal de las asociaciones de obreros y la ampliación del derecho de sufragio.

B) la eliminación de los privilegios de la nobleza y la abolición del derecho a la propiedad privada.

C) el reconocimiento legal de los sindicatos de obreros y la abolición de la esclavitud en Europa.

D) el establecimiento del derecho al sufragio censitario y el reconocimiento de la libertad de imprenta.

PREGUNTA 69 :

Después de la Primera Guerra Mundial, se firmó el Tratado de Saint-Germain-en-Laye, entre las potencias aliadas y Austria. En este acuerdo, se estableció el desmembramiento de la antigua monarquía de los Habsburgo y la prohibición de revisar o revocar la independencia de Austria, esto con el fin de impedir

A) la creación de los estados de Eslovaquia y Yugoslavia.

B) una terrible unión política y económica con Alemania.

C) una posible alianza con países germanos, como Bulgaria.

D) el dominio del Imperio Austro-Húngaro sobre Alemania.

CLAVES DE HISTORIA: 65)B 66)C 67)D 68)A 69)B

CLIC AQUÍ Ver LO DE HISTORIA SOLUCIONES

GEOGRAFÍA

PREGUNTA 70 :

Se requiere saber la distancia que un bote recorrerá de ida y vuelta entre dos pueblos de Loreto. En un mapa a escala 1:75,000, la longitud del río con sus meandros totaliza 60 cm. El motor del bote emplea 12 gl. de combustible por hora de funcionamiento y se estima que en la ida (contra corriente) el bote irá a una velocidad media de 15 km/h y, en el retorno, a 20 km/h. El combustible cuesta S/15.00 el galón. La distancia entre los pueblos es de ___ km, el tiempo de ida y vuelta es de _____ , y el costo total del combustible ___ soles.

A) 75 - 10 h 10 m - 790

B) 60 - 4 h 05 m - 1,260

C) 90 - 10 h 30 m - 1, 890

D) 45 - 5 h 15 m - 945

PREGUNTA 71 :

El cambio climático (CC) que se experimenta en las últimas décadas se prevé como un proceso que puede resultar catastrófico para la humanidad en su conjunto. Se caracteriza en gran parte por un aumento rápido y global de las temperaturas, proceso que se debe a una serie de factores y hechos concomitantes. Marque la alternativa que contiene características propias y consecuencias de este proceso.

I. El CC se debe al aumento del contenido de gases de efecto invernadero y, tiene entre sus consecuencias, la reducción de los hielos cuaternarios y el permafrost.

II. El CC generará un aumento del nivel marino, que afectará directamente a países como Indonesia, Fiji, Holanda, Paraguay y Suiza, entre otros.

III. En las punas altas de los Andes, el CC puede causar el retroceso y desaparición de glaciares, pero a la vez puede hacer que se cultive en zonas cada vez más altas.

lV. El CC va a causar, en todo el mundo, un aumento de inundaciones, nuaycos, erosión de tierras y movimientos de masa de alto riesgo.

A) Solo I y III

B) I, II y III

C) II, III y IV

D) I y IV

PREGUNTA 72 :

Los meridianos y paralelos permiten ubicar, geográficamente, cualquier punto o área sobre la superficie terrestre, calcular distancias, extensiones, etc. mediante las coordenadas de latitud y longitud. Al respecto, identifique la alternativa que contiene las características del sistema de ubicación por coordenadas geográficas.

I. La latitud de un punto en la superficie terrestre es el arco de meridiano que hay entre ese punto y la línea ecuatorial.

II. La longitud de un punto en la superficie terrestre es el arco de paralelo que hay entre ese punto y el meridiano de Greenwích.

III. Hay infinitos meridianos y todos son circunferencias máximas.

IV. Hay infinitos paralelos y todos son circunferencias máximas.

A) I, II y III

B) II, III y IV

C) Solo III y IV

D) Solo I y II

PREGUNTA 73 :

En relación con los procesos y hechos geográficos del Perú, marque la respuesta correcta.

A) El alto riesgo sísmico de la costa se debe a su cercanía y a la convergencia de placas, siendo mayor en los sectores de las ciudades en montañas rocosas que en los suelos arenosos.

B) Los suelos aluviales de la costa son más fértiles y productivos que los suelos aluviales de la selva, ya que estos últimos se tornan muy ácidos por el lavado que le ocasionan las lluvias.

C) El crecimiento económico que se requiere generará una mayor demanda de energía. Al respecto, nuestro país es uno de los más altos en reservas comprobadas de petróleo.

D) El extremo centralismo peruano, se expresa en que la capital tiene tres veces más población que la segunda, tercera y cuarta ciudades del interior (Arequipa, Trujillo y Chiclayo).

CLAVES DE GEOGRAFÍA: 70)D 71)A 72)D 73)B

CLIC AQUÍ Ver LO DE GEOGRAFÍA SOLUCIONES

ECONOMÍA

PREGUNTA 74 :

En los primeros días del año 2022, Apple logró ser la primera empresa a nivel mundial en valer US$3 billones. El hecho de que en la mayoría de los países se impusieran confinamientos para frenar el coronavirus, generó que los usuarios incrementaran sus gastos en dispositivos como computadoras portátiles, tabletas y teíéfonos inteligentes, así es que en solo dieciséis meses, Apple logró que su valoración bursátil aumentara en un billón. Sobre la base de lo planteado, cada una de las medidas de confinamiento obligatorio decretada por los gobiernos puede ser considerada para Apple como

A) una aplicación del teorema de Coase.

B) un caso de reducción de costes de transacción.

C) una externalidad negativa en el consumo.

D) una externalidad positiva en la producción.

PREGUNTA 75 :

El 2 de enero del 2020. el diario La República publicó la siguiente nota: «Del total de 4266 investigadores con calificación Renacyt (Registro Nacional de .Ciencia, Tecnología y de Innovación Tecnológica) a nivel nacional, 386 corresponden a docentes investigadores de la Universidad Nacional Mayor de San Marcos (UNMSM). Gracias a ello, la Decana de América lidera el top de las 5 universidades que ostentan los mayores números de investigadores». Algunas de las investigaciones de la comunidad sanmarquina están orientadas, por supuesto, a generar actividades productivas, lo que implica un conocimiento de las etapas de un proyecto de inversión. A continuación, seleccione el pareado correcto.

I. Idea

II. Preinversión

III. Inversión

IV. Operación

a. Ejecución de la inversión ya materializada, el negocio está en marcha, generando el bien o servicio

b. Materialización antes de inicio de actividades, proceso de implementación del proyecto

c. Estudio de viabilidad económica con información estadística, proyección de costos y beneficios

d. Estudios preliminares. Se busca consolidar la idea del proyecto y limitar los márgenes de la inversión

A) Id, IIc, IIIb, IVa

B) la, IId, IIIc, IVb

C) la, IIc, IIIb, IVd

D) lb, IIc, IIId, IVa

PREGUNTA 76 :

Un organismo regulador y una empresa monopólica natural encargada de brindar un servicio de mucha importancia para la población, acuerdan establecer una tarifa o precio en un nivel tal que la empresa obtenga sólo beneficios contables mas no beneficios económicos. En dicho escenario, si se generase un aumento en la demanda de mercado, en cumplimiento del citado acuerdo, el Organismo regulador dispondría

A) aumentar la tarifa.

B) mantener la tarifa.

C) reducir la producción.

D) reducir la tarifa.

PREGUNTA 77 :

De acuerdo con el tema de la informalidad, establezca la relación correcta entre los conceptos y las definiciones correspondientes.

I. Sector informal

II. Economía informal

III. Empleo informal

a. Compuesto por el sector informal y el empleo informal

b. Unidades productivas no registradas en la SUNAT

c. Trabajadores y empleadores dueños de su propia empresa del sector informal

d. Empleo sin beneficios (seguridad social, licencia por enfermedad, etc.)

A) Ia, IIb, IIIc, IVd

B) Ib, IIa, IIId, IVc

C) Ic, IId, IIIa, IVb

D) Id, IIc, IIIb, IVa

CLAVES DE ECONOMÍA: 74)D 75)A 76)D 77)B

CLIC AQUÍ Ver LO DE ECONOMÍA SOLUCIONES

FILOSOFÍA

PREGUNTA 78 :

Yo no he sido jamás maestro de nadie. Si cuando yo estaba hablando y me ocupaba de mis cosas, alguien deseaba escucharme, jamás se lo impedí. Tampoco dialogo cuando recibo dinero, ni dejo de dialogar si no lo recibo, antes bien, me ofrezco para que me pregunten, tanto al rico como al pobre, y lo mismo si alguien prefiere escuchar y responder mis preguntas. Si alguno de estos es, luego, un hombre honrado o no lo es, no podría yo, en justicia, incurrir en culpa; les gusta oírme examinar a los que creen ser sabios y no lo son, este trabajo me ha sido encomendado por el dios.

Adaptado de Platón (2021) Apología de Sócrates, en Platón 1, Gredas

Determine el valor de verdad (V o F) de los enunciados.

I. Sócrates rechaza la enseñanza remunerada de los sofistas.

II. La actividad filosófica para Sócrates es interrogativa y crítica.

III. La responsabilidad ética es personal e intransferible.

A) VVV

B) VVF

C) FVV

D) VFV

PREGUNTA 79 :

En la actualidad, muchos jóvenes piensan que la felicidad consiste en llevar una vida sensual y en acumular riquezas. En eso consiste para ellos, además, una vida exitosa y plena. En cambio, Aristóteles sostuvo que la felicidad humana consiste en

A) contemplar la idea del bien y gobernar la ciudad.

B) alcanzar la imperturbabilidad de la propia alma.

C) recibir los honores y reconocimiento de los demás.

D) vivir las pasiones bajo el gobierno de la razón.

PREGUNTA 80 :

En la Suma Teológica, Tomás de Aquino propuso cinco vías para demostrar la existencia de Dios. En la tercera vía, parte de la existencia de entes contingentes, es decir, de entes que pueden ser o no ser. Hay entes que alguna vez no fueron y han llegado a ser, y entes que son y dejarán de existir alguna vez. Si todos los entes fueran contingentes, alguna vez no existieron y nada existiría ahora. Por lo tanto, tiene que existir un ser no contingente sino necesario y a tal ser los hombres le llaman Dios.

En esta demostración, la conclusión se apoya en

A) la crítica tomista a la eternidad del mundo.

B) la autoridad dogmática de los escolásticos.

C) la reducción al absurdo.

D) la ontología escolástica del siglo XIII.

PREGUNTA 81 :

Luis lee con mucha atención las Meditaciones metafísicas de Descartes y queda fascinado con el proceso de la duda presentado por este autor en la primera parte del texto. A diferencia de la duda ordinaria, la duda cartesiana es un

A) medio para desechar lo probable y acceder a una verdad absoluta.

B) proceso para alcanzar el ideal ético de la imperturbabilidad del alma.

C) ejercicio que pretende afirmar nuestras creencias y voliciones.

D) método para validar y fortalecer nuestras opiniones empíricas.

CLAVES DE FILOSOFÍA: 78)A 79)D 80)C 81)A

CLIC AQUÍ Ver LO DE FILOSOFÍA SOLUCIONES

FÍSICA

PREGUNTA 82 :

El pistón de un dispositivo eléctrico oscila con un movimiento armónico simple de modo que su posición varía de acuerdo con la ley x(t) = (√2cm)cos(ωt+π/4), donde x está dado en centímetros y t en segundos. Si la velocidad media del pistón para un intervalo de tiempo varia entre t = 0,0 s y t = 1,0 s es –1,0 cm/s, determine el valor de la frecuencia angular de la oscilación.

A) (π/2) rad/s

B) (π/4) rad/s

C) (3π/4) rad/s

D) (3π/2) rad/s

PREGUNTA 83 :

La temperatura de tres líquidos diferentes, A, B y C, de masas iguales, es 12, 18 y 28 °C respectivamente. Cuando A y B sean mezclados, la temperatura final de equilibrio es 16 °C. Cuando B y C sean mezclados, la temperatura de equilibrio es 23 °C. ¿Cuál será la temperatura de equilibrio cuando A y C sean mezclados?

A) 20,0 °C

B) 22,7 °C

C) 17,3 °C

D) 25,4 °C

PREGUNTA 84 :

El corazón humano bombea, según la Fundación Española del Corazón, 5 litros de sangre por minuto. Según el Texas Heart Institute, si el corazón fuese una fuente, su potencia haría que la sangre alcance los 10 metros de altura. A partir de estos datos, estime la potencia del corazón humano.

Datos: g = 10 m/s²; ρsangre = 1,05 g/cm³

A) 17,5 W

B) 12,5 W

C) 8,75 W

D) 4,38 W

PREGUNTA 85 :

Una moneda pesada cae al fondo de un recipiente, el cual contiene dos líquidos A y B no miscibles (ρA = 800 kg/m³ ; ρB = 1200 kg/m³ ), como muestra el gráfico. Si se conoce que la presión atmosférica local es de 100 kPa, determine lo siguiente: la presión absoluta que la moneda experimentará y la altura que el líquido B debería tener para que la moneda experimente la misma presión en ausencia del líquido A.

Dato: g = 10 m/s²

A) 106,4 kPa y 4/30 m

B) 6,4 kPa y 8/15 m

C) 6,4 kPa y 4/30 m

D) 106,4 kPa y 8/15 m

PREGUNTA 86 :

Durante una clase de laboratorio, dos alumnos conectan dos condensadores 6 μF cada uno, en serie, y los cargan a una diferencia de potencial de 12 V. Al releer el manual, se dan cuenta de que debieron conectar los condensadores en paralelo, pero, para no desconectar todo, deciden cambiar la diferencia de potencial para llegar a almacenar la misma energía que con el montaje original. ¿Cuál debería ser dicha diferencia de potencial?

A) 24 V

B) 6 V

C) 26 V

D) 48 V

PREGUNTA 87 :

Una partícula de 100 g de masa se mueve sobre la parte interior de una superficie semiesférica lisa de radio r, como muestra la figura. La trayectoria de la partícula es una circunferencia que está en un plano horizontal cuya distancia al punto más bajo de la superficie es 0,1 m. Si la partícula gira con rapidez constante, identifique la afirmación o afirmaciones correctas.

Dato: g = 10 m/s²

I. La fuerza centrípeta sobre la partícula es 0,75 N.

II. La velocidad angular de la partícula es 3,0 rad/s.

III. La componente vertical de la fuerza de reacción del piso es 1,0 N.

A) II y III

B) Solo I

C) I y III

D) I y II

PREGUNTA 88 :

De acuerdo con el principio de incertidumbre, es imposible medir, simultáneamente, la posición y la cantidad de movimiento de una partícula con precisión. En este contexto, si una bala de masa m = 0,02 kg, velocidad de magnitud 500 m/s, medida con una precisión dentro de 0,010%, ¿en qué límites es posible determinar la posición de la bala con los datos?

Dato: h/2𝛑 = h = 1,00 × 10−³⁴ J · s

A) 5,00 × 10−³¹ m

B) 5,00 × 10−³² m

C) 1,00 × 10−³¹ m

D) 5,00 × 10−³³ m

CLAVES DE FÍSICA: 82)B 83)B 84)C 85)D 86)A 87)C 88)B

CLIC AQUÍ Ver LO DE FÍSICA SOLUCIONES

QUÍMICA

PREGUNTA 89 :

Para preparar soluciones, en los laboratorios de química, se usan solutos como el hidróxido de calcio. Determine la concentración molar de una solución de este soluto si se disuelve en agua 1,48 gramos de Ca(OH)₂ para obtener 10 litros de solución.

Dato: P.F. Ca(OH)₂ = 74

A) 2,0 × 10−³

B) 1,0 × 10−³

C) 4,0 × 10−³

D) 3,0 × 10−³

PREGUNTA 90 :

Indique el nombre correcto del siguiente compuesto orgánico oxigenado:

A) Ácido 3 – fenilhexanoico

B) Ácido 4 – fenilpentanoico

C) Ácido 4 – ciclohexilhexanoico

D) Ácido 3 – ciclohexilpentanoico

PREGUNTA 91 :

En el Perú, con el fin de obtener metales como oro, plata, cobre, zinc, plomo, molibdeno, entre otros, se procesan diferentes tipos de minerales y, para concentrarlos, se desarrollan procesos físicos, químicos, fisicoquímicos y biológicos. Identifique los principales procesos que se realizan, en nuestro país, para la extracción del oro.

A) Tostación - calcinación

B) Cianuración - amalgación

C) Biolixiviación - electrólisis

D) Molienda - flotación

PREGUNTA 92 :

Cuando la temperatura y la presión cambian al mismo tiempo, es posible calcular el nuevo volumen. En tal sentido, si un gas que inicialmente ocupa 50 litros a 2,50 atmósferas y 27 °C es sometido a 1,50 atmósferas y 177 °C, ¿qué volumen, en litros, ocupará?

A) 100

B) 150

C) 175

D) 125

PREGUNTA 93 :

La hematita (Fe₂O₃) es utilizada como materia prima para la obtención del hierro elemental. En la industria, se procesa en hornos eléctricos a temperaturas elevadas.

1 Fe₂O₃ + 3CO → 2Fe + 3CO₂

Considerando la ecuación química, complete, en forma secuencial, los espacios libres de cada uno de los enunciados.

I. Al reaccionar 800 gramos de Fe₂O₃ con 20 mol CO, se tiene un exceso de ________.

II. Se produce 6 mol de CO₂, cuando el rendimiento es de 80%, al añadir ________.

III. En el proceso óxido-reducción, el CO es el reactante considerado como ________.

Dato: P.F. Fe₂O₃=160

A) 200 g Fe₂O₃ - 256 g Fe₂O₃ - agente oxidante

B) 5 mol CO - 400 g Fe₂O₃ - agente reductor

C) 200 g Fe₂O₃ - 400 g Fe₂O₃ - agente oxidante

D) 5 mol CO - 256 g Fe₂O₃ - agente reductor

PREGUNTA 94 :

Mediante la electrólisis, un proceso no espontáneo, se convierte la energía eléctrica en energía química. Determine el número de moles de átomos obtenidos en cada una de las tres celdas dispuestas en serie y en cuyo circuito se hace circular 10 faraday: en el ánodo de la celda que contiene cloruro de magnesio fundido, en el cátodo de la celda que contiene sulfato cúprico acuoso y en el ánodo de la celda que contiene agua acidulada respectivamente.

A) 5 - 10 - 5

B) 20 - 10 - 10

C) 10 - 20 - 10

D) 10 - 5 - 5

CLAVES DE QUÍMICA: 89)A 90)C 91)B 92)D 93)B 94)D

CLIC AQUÍ Ver LO DE QUÍMICA SOLUCIONES

BIOLOGÍA

PREGUNTA 95 :

Las bacterias son células procariotas que pueden desarrollar estructuras de resistencia que les permiten subsistir en condiciones ambientales diversas, como en el intestino de un insecto atrapado en ámbar por más de 300 años. ¿Qué estructura les confiere esa capacidad?

A) La espora

B) La cápsula

C) La pared celular

D) Los pilis

PREGUNTA 96 :

Cuando se analizan los restos fósiles hallados en diferentes partes del mundo, se puede inferir la morfología y las características del ambiente en que vivieron los organismos extintos, lo que permite la reconstrucción del pasado. Por ello se denominan

A) mecanismos de evolución.

B) evidencias de evolución.

C) patrones de evolución.

D) macroevolución.

PREGUNTA 97 :

Con respecto a la circulación de la sangre en el corazón y pulmones, seleccione la alternativa correcta sobre los enunciados.

I. La válvula tricúspide se abre para que la sangre venosa pase al ventrículo derecho.

II. La válvula mitral se abre para que la sangre arterial pase al ventrículo izquierdo.

III. La válvula pulmonar se abre para que la sangre arterial se dirija a los pulmones.

A) VFF

B) VVF

C) VVV

D) FVF

PREGUNTA 98 :

Para graduarse de ingeniero ambiental, José investiga una bacteria aislada de aguas residuales que oxida el sulfuro de hidrógeno (H₂S) proveniente de la descomposición de materia orgánica y obtiene así la energía sin utilizar la luz del Sol. El tipo de nutrición empleado por esta bacteria es

A)· heterótrofa y saprofítica.

B) autótrofa y fotosintética.

C) autótrofa y quimiosintética.

D) autótrofa y saprofítica.

PREGUNTA 99 :

Durante una excursión a la selva central, los estudiantes observaron unas plantas que flotaban sobre las aguas de una laguna. Tomaron algunas muestras y las llevaron al laboratorio para examinar sus tejidos. Descubrieron que, desde las hojas hasta la raíz, había un tejido con grandes espacios vacíos entre las células. ¿Qué tipo de tejido observaron los estudiantes?

A) Epidermis acuífera

B) Parénquima de reserva

C) Parénquima acuífero

D) Aerénquima

PREGUNTA 100 :

En la selva peruana, existen distintas poblaciones humanas autóctonas que conviven con diversas poblaciones de animales, plantas y microorganismos de distintas especies. Todas ellas comparten áreas de suelo para tomar sus nutrientes, aprovechan el agua de los ríos y lagunas cercanas y se abastecen de los mismos frutos y especies. ¿En qué nivel de organización biológica podemos considerar a la selva peruana?

A) Biósfera

B) Ecosistema

C) Comunidad

D) Población

CLAVES DE BIOLOGÍA: 95)A 96)B 97)B 98)C 99)D 100)B

CLIC AQUÍ Ver LO DE BIOLOGÍA SOLUCIONES

HABILIDAD VERBAL

TEXTO 1

TEXTO A

La naturaleza ya no es palpable ni intuitiva, aunque ello no preocupa al científico que quiere saber cómo funciona —o sea, su ley— y que hoy, además de buscar leyes cada vez más precisas y abarcadoras, apunta a lo radicalmente nesesario. En efecto, antes anhelaba descubrir leyes cuya contingencia, empero, dejaba a Dios el papel de demiurgo, quien las había creado a su antojo, pero ahora busca una ley de leyes que sea absolutamente necesaria. Por ejemplo, la partícula de Dios, la partícula elemental llamada también Bosón de Higgs, que corrobora el modelo básico del universo para la física, es un pilar de la teoría que pretende reducir a cero el libre albedrío divino, al demostrar que no vivimos en el mejor mundo posible, sino en el único, ya que es necesariamente así.

Adaptado de Arenas, G. (2014). «Una Brújula defectuosa». En Lo real puesto al día, en el siglo XXI. EOL.

TEXTO B

La ciencia, desde luego, impone la dictadura de sus criterios sobre lo real, con los cuales quiere liberarse del malentendido y llegar a una universalización respecto de cómo entenderlo. Sin embargo, al mismo tiempo, encuentra dificultades para precisar qué es real. Si se escucha a los científicos o a los epistemólogos contemporáneos, la materia ha estallado y ahora falla todo lo que antes definía lo real de modo unívoco. A pesar de las tentativas de afirmar que, si es científico, es verdad, un cierto caos se hace evidente como resultado de los hallazgos actuales de investigación, abriendo nuevamente la pregunta por la verdad. Esto me hace decir que es el fin de la doxa cartesiana. [...] hoy la epistemología es poscartesiana. ¿Qué funciona ahora como criterio de verificación de lo real?

Adaptado de Brousse, M-H. (2014). «Atraparlo por los trozos». En Lo real puesto al día, en el siglo XXI. EOL.

PREGUNTA 1 :

En relación con la ciencia, la diferencia entre los dos textos radica en que el

A) segundo añade que esta disciplina se enfrenta a una crisis respecto de la posibilidad de la univocidad.

B) primer texto asume que esta disciplina, la ciencia, es actualmente de tendencia postcartesiana.

C) objetivo de la disciplina ha virado su propósito: de la búsqueda de certeza al hallazgo de incertidumbres.

D) segundo texto propone que las leyes generales y necesarias es el objetivo de la disciplina científica.

PREGUNTA 2 :

En el texto A, la palabra ANTOJO adquiere el sentido de

A) capricho pasajero.

B) decisión arbitraria.

C) juicio insuficiente.

D) deseo vehemente.

PREGUNTA 3 :

Ambos textos coinciden en presentar el carácter de la ciencia como una actividad

A) relacionada con la religión.

B) dogmática en sus leyes.

C) que ya no busca certezas.

D) de constante investigación.

PREGUNTA 4 :

Cabe inferir que, según el texto A, «la partícula de Dios» forma parte del proyecto científico que tiene por objetivo

A) anular o, por lo menos, disminuir la apelación a lo aleatorio en las explicaciones científicas.

B) conocer más profundamente las implicaciones de los fenómenos aleatorios del universo.

C) replicar los distintos elementos subátomicos de la materia y establecer una teoría unificada.

D) cuestionar la idea de la intervención divina en los procesos físicos que hoy son explicados.

PREGUNTA 5 :

Cabe inferir que, desde la perspectiva del texto B, en la ciencia se aloja una contradicción entre

A) los propósitos teóricos y los descubrimientos de la física actual.

B) la creencia en la autoridad científica y las posibilidades de explicación.

C) el afán por leyes unívocas y el caos o la dispersión de los hallazgos.

D) el imperativo cognitivo y las posibilidades instrumentales actuales.

TEXTO 2

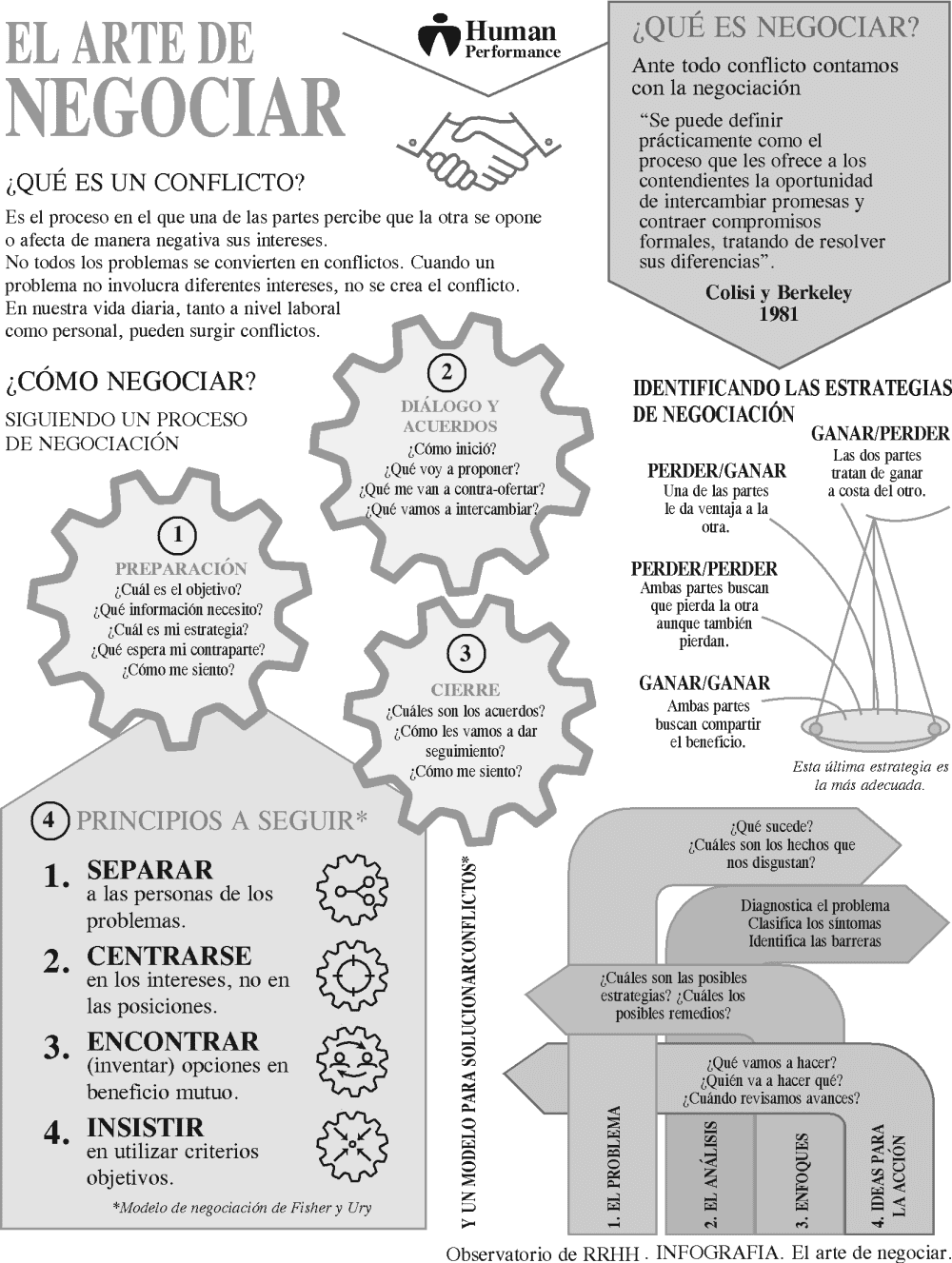
PREGUNTA 6 :

El principal propósito de la infografía es

A) contribuir a que las dos partes de un conflicto salgan siempre favorecidas.

B) analizar las distintas fases durante el proceso de una negociación.

C) identificar las preguntas frecuentes antes de resolver un conflicto.

D) señalar los aspectos relevantes a tomar en cuenta en una negociación.

PREGUNTA 7 :

De acuerdo con lo planteado en la infografía, se infiere que, para enfrentar exitosamente los conflictos, deberíamos

A) sopesar lo que vamos a ganar y lo que la otra parte perderá en la contienda.

B) aprender a expresar nuestros puntos de vista y escuchar los de los demás.

C) apartar las cuestiones emocionales, pues afectan la objetividad del propósito.

D) comprobar que una de las partes involucradas afecta los intereses de la otra.

PREGUNTA 8 :

En el título del material informativo, la palabra ARTE se emplea para

A) comparar el ingenio con la invención de estrategias de negociación.

B) llamar la atención de un público aficionado a la actividad artística.

C) destacar que la negociación es una capacidad o habilidad humana.

D) proponer que negociar también puede ser una actividad creativa.

PREGUNTA 9 :

El uso del engranaje como elemento organizador de la información tiene como propósito

A) hacer un paralelo con la manera en que las partes encajan para lograr mover un mecanismo.

B) establecer una correspondencia entre el arte de negociar y la organización dentro de una fábrica.

C) brindar la idea de negociar como un proceso cíclico en el que las dos partes se retroalimentan.

D) utilizar una forma atractiva para que la composición tenga un mayor impacto visual para el lector.

PREGUNTA 10 :

Determine el valor de verdad (V o F) de los siguientes enunciados

I. Respecto del modelo para solucionar conflictos, es erróneo sostener que las contingencias no están contempladas como parte de los enfoques.

II. La lectura de la infografía permite conocer las posibles maneras de solucionar conflictos laborales que impliquen dos puntos de vista distintos.

III. Entre las estrategias para resolver una negociación se considera que la más adecuada es la que logra como resultado el equilibrio entre las partes.

A) FVV

B) VFV

C) VVF

D) VVV

INGLÉS

TEXTO 3

Scientists are particularly interested in the brains of people who speak more than one language fluently because that skill is hard to acquire after about age seven. In one of Kuhl's studies, for example, native Mandarin Chinese speakers spoke Chinese to nine-month-old American babies for twelve sessions over four weeks. Each session lasted about 25 minutes. At the end of the study, the American babies responded to Mandarin sounds just as well as did Chinese babies who had been hearing the language their entire lives. (English-speaking teenagers and adults would not perform nearly as well.)

If a child regularly hears two languages, his brain forms a different pathway for each language. However, once the brain solidifies those electrical language pathways by around age seven, it gets harder to form new ones. By then, a baby's brain has disposed of, or pruned, all the unnecessary connections that the infant was born with. So, if you don’t start studying Spanish or Russian until middle school, you must struggle against years of brain development, and progress can be frustrating. A twelve-year-old’s brain has to work much harder to forge language connections than an infant’s brain does. “We ought to be learning new languages between ages zero and seven, when the brain does it naturally”, Kuhl says.

Adapted from Lee, L. and Gundersen, E. (2011). Select Readings Intermediate (2nd Ed.). Oxford University Press.

PREGUNTA 11 :

The passage is primarily concerned with which of the following statements?

A) Foreign language learning is a very difficult task to do.

B) Spanish and Russian have to be learnt when you are a child.

C) American babies are more intelligent than Chinese babies.

D) It’s easy to learn a foreign language when you are very young.

PREGUNTA 12 :

As it is used in the text, the term FORGE can be best described as to

A) cut off something.

B) to clean it to make it work.

C) make something work.