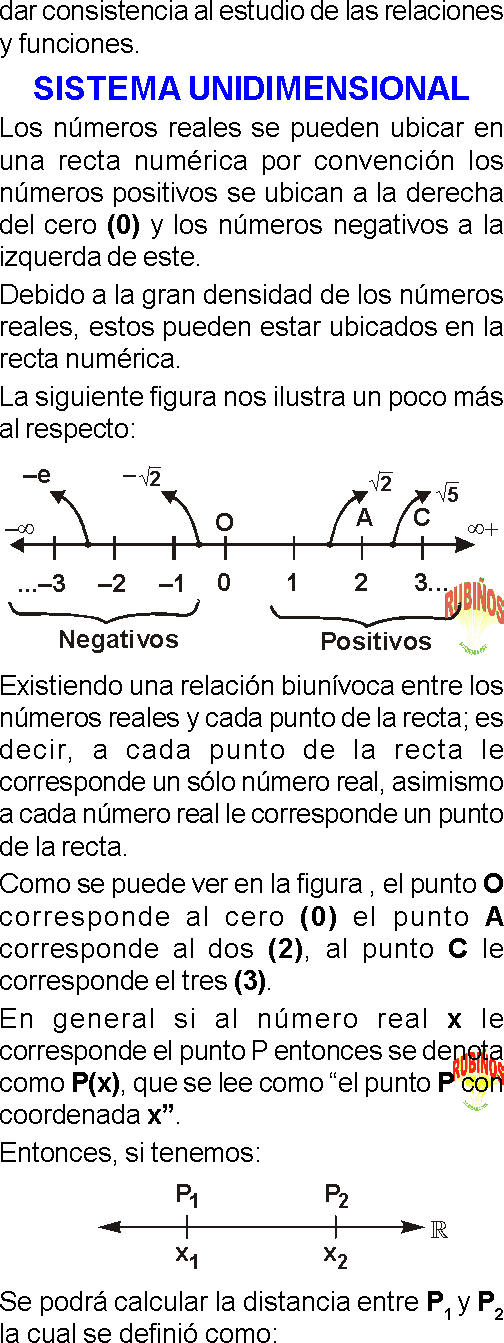
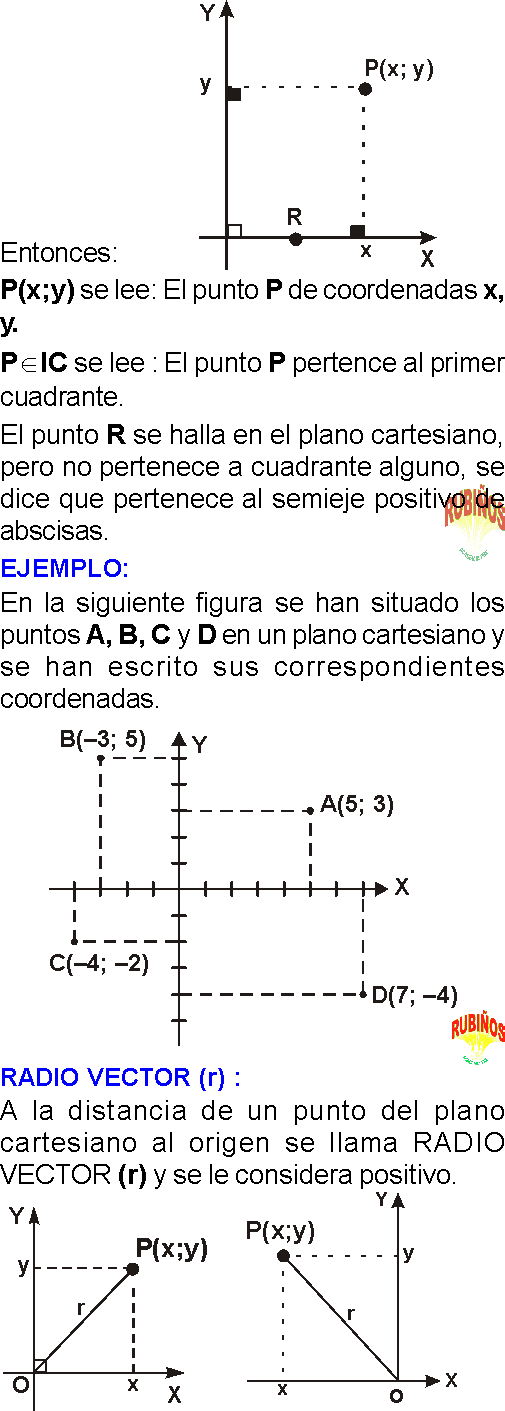
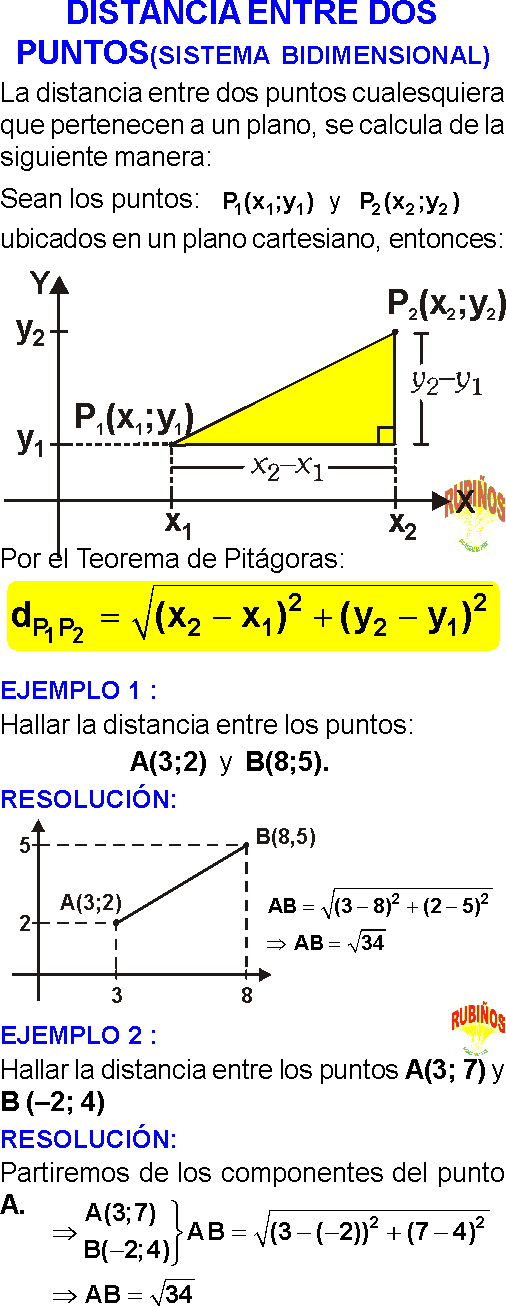
GEOMETRÍA ANALÍTICA EJERCICIOS RESUELTOS PDF

La geometría analítica es una rama de las matemáticas que combina el álgebra y la geometría para estudiar figuras y relaciones en un plano o en el espacio, utilizando un sistema de coordenadas. Este enfoque permite representar gráficamente ecuaciones algebraicas y resolver problemas geométricos mediante cálculos algebraicos.
RELACIÓN ENTRE ÁLGEBRA Y GEOMETRÍA: 
Las ecuaciones algebraicas (como líneas rectas, parábolas, circunferencias) pueden representarse en un plano cartesiano. Las propiedades geométricas de figuras se analizan a través de ecuaciones. 

APLICACIONES DE LA GEOMETRÍA ANALÍTICA: 
• Análisis de trayectorias y movimientos en física. 
• Diseño y cálculo de estructuras en ingeniería. 
• Representación de datos en ciencias y economía. 
• La geometría analítica es fundamental para estudiar cómo las figuras y las ecuaciones están interrelacionadas.
PROBLEMAS RESUELTOS
PREGUNTA 1 : 
Hallar la distancia entre los puntos, cuyas coordenadas son: (0;3) y (– 4;1)
A) 2√3 
B) 2√5 
C) 3 
D) 5 
E) 3√2 
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 2 : 
Un triángulo ABC tiene por coordenadas A(– 5;1) , B(– 5;4) y C( 2;4). 
Calcular el área del triángulo. 
A) 10,5 u² 
B) 12,5 u² 
C) 14,5 u² 
D) 16 u² 
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 3 : 
Si A(1;3) y B(2;–5) son los puntos extremos del segmento AB, halle la suma de las coordenadas del punto de trisección más próximo al extremo A. 
A) –1/3 
B) 5/3 
C) –2/3 
D) –5/3 
E) 2/3 
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 4 :
Sean los puntos A(1;3), B(5;2). El punto C está ubicado en el primer cuadrante, sobre la recta ℒ de ecuación y=x+3, de modo que el área de la región triangular ABC es 9,5 u². Calcule la suma de las coordenadas del punto C. 
A) 11 
B) 9 
C) 13 
D) 15 
E) 17 
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 5 : 
Las rectas
se intersecan formando una región triangular. Halle su área en m². 
A) 4 
B) 6 
C) 3 
D) 5 
E) 2 
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 6: 
En la figura dada, halle la ecuación de la recta L2 que pasa por el punto A(2;6) y es perpendicular a la recta L1. 
A) 4x + 3y= 26 
B) 3x + 4y = 26 
C) 4x − 3y = 23 
D) 3x − 4y = 23 
E) 5x − y = 26 
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 7 : 
¿ Cuál es la ecuación de la recta que pasa por el origen y es perpendicular a la recta 
3x–2y = 6 ? 
A) 2x + 3y = 0 
B) 3x + 2y = 1 
C) 2x – 3y = 6 
D) 3x + 4y = 2 
E) 2x – 3y = 4 
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 8 : 
Una recta pasa por el diámetro de la circunferencia 
x² + y² – 6x + 4y –12 = 0 y biseca a la cuerda cuya ecuación es x+3y – 6= 0. 
La ecuación de dicha recta es: 
A) –2x+y –1=0 
B) –x+3y –11=0 
C) –2x+3y –11=0 
D) 3x–y –11=0 
E) 3x+2y – 6=0 
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 9 : 
Si las rectas 
ℒ1 : x – 4y + 3 = 0
ℒ2 : 4x + y – 5 = 0
son tangentes a una circunferencia en los puntos P1(5;2) y P2(2;–3) respectivamente, entonces la suma de las coordenadas del centro de la circunferencia es: 
A) 3 
B) 4 
C) 5 
D) 6 
E) 7
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 10 : 
En la figura se representa un pozo de agua que tiene forma parabólica, donde A(8;y) , B(12;0), C( –12;0) y el vértice de la parábola V(0;– 18). 
Halle el valor de y.
A) – 8 
B) – 12 
C) – 9 
D) – 10 
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 11 : 
La recta ℒ : x – 2y + 4 = 0 interseca a la parábola P: y²=4px en el punto (a;4). 
Calcule la distancia del foco de P a la recta ℒ. 
A) 3 u 
B)√5 u 
C) 2 u 
D) 2√5 u 
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 12 : 
La ecuación de la elipse es 
La distancia del centro de la elipse a una cuerda AB paralela al eje mayor y de longitud a es
A) √3b/2
B) √5b/7
C) 3b/2
D) b/2
E) b/4
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 13 : 
La figura representa un parque de forma elíptica. Colocamos su centro en el origen de coordenadas y su eje mayor contenido en el eje X. Si se sabe que el borde elíptico pasa por los puntos P(10√6; −10) y Q(20; 10√2) , halle su ecuación. 
A)  [x²/800 ] + [y²/400 ] =1
B)  [x²/800 ] + [y²] =1
C)  [x²/400 ] + [y²/200 ] =1
D)  [x²/300 ] + [y²/900 ] =1
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 14 : 
Las rectas 3y–x–6=0, x=0, y=0 determinan una región triangular. 
Al hacer girar esta región alrededor del eje X se genera un sólido de revolución. 
Calcule el volumen de dicho sólido. 
A) 24𝛑u³ 
B) 6𝛑u³ 
C) 8𝛑u³ 
D) 18𝛑u³  
RESOLUCIÓN :
Rpta. : "C"
Para llegar al actual proceso de resolución de la ecuación ax+b=c han pasado más de 3000 años. 
Los egipcios nos dejaron en sus papiros (sobre todo en el de Rhind –1650 a.n.e. y el de Moscú –1850 a.n.e.), multitud de problemas matemáticos resueltos. 

La mayoría de ellos son de tipo aritmético y respondían a situaciones concretas de la vida diaria; sin embargo, encontramos algunos que podemos clasificar como algebraicos, pues no se refiere a ningún objeto concreto. 

En éstos, de una forma retórica, obtenían una solución realizando operaciones con los datos de forma análoga a como hoy resolvemos dichas ecuaciones. 

Las ecuaciones más utilizadas por los egipcios eran de la forma: 
x+ax=b 
x+ax+bx=c
Donde a, b y c eran números conocidos y x la incógnita que ellos denominaban aha o montón. 

Una ecuación lineal que aparece en el papiro de Rhind responde al problema siguiente:
 “Un montón y un sétimo del mismo es igual a 24”
Como alumno primero, como profesor después y como lector pertinaz de textos de ciencia, debo decir que hasta hoy la mejor bibliografía existente para el área de geometría se reduce a un conocido número de libros extranjeros: españoles, franceses, americanos y rusos. 

Ninguno de ellos brindó al docente la totalidad de temas que se desarrollan en nuestro país para efectos de una preparación preuniversitaria. 
Nosotros pretendemos que esta obra logre cubrir esta necesidad y aportar luces allí donde creemos que falta claridad en el debate y organicidad en la disciplina. 

Durante mucho tiempo, en nuestro país, se ha creído o se ha hecho creer que la geometría es una disciplina de la matemática cuya enseñanza puede hacerse omitiendo su estructura axiomática. 
Esto se revela principalmente en el listado de sus contenidos, en el orden de su desarrollo, en el método de su enseñanza y en el campo de su aplicación, en la mayoría de las instituciones educativas, sean estas colegios, academias o centros preuniversitarios de las propias universidades. 
La enseñanza actual de la geometría ha dejado de lado la formalidad y la demostración, acciones que redundan en una insuficiente información y formación por parte del educando. 
Lamentamos que esto esté ocurriendo y no se haya hecho nada hasta hoy para corregirlo. 

Estamos seguros que no es nada bueno, para la educación en general, prescindir de una importantísima herramienta matemática que, al margen de ayudarnos a comprender los cimientos de esta ciencia y resolver problemas, contribuye generosamente a desarrollar capacidades matemáticas en las personas que la estudian, habilidades que luego le permiten insertarse adecuadamente a)os niveles superiores del mundo intelectual y laboral.

Ejercicios resueltos de examen de admisión a la Universidad