HIPÉRBOLA EJERCICIOS RESUELTOS PDF
ECUACIÓN CANÓNICA ORDINARIA Y GENERAL APLICACIONES–GEOMETRÍA ANALÍTICA
PRIMERA PRACTICA
PREGUNTA 1 :
Halle la ecuación de la hipérbola equilátera con centro en el origen y que pasa por el punto (5; – 3).
A) x² – y² = 8
B) x² – y² = 10
C) x² – y² = 8
D) x² – y² = 1
E) ) x² – y² = 16
Rpta. : "E"
PREGUNTA 2 :
Halle las ecuaciones de las asíntotas de la curva : 144x² – 25y² = 3600
A) 2x ± 15y = 0
B) 5x ± 12y = 0
C)12x± 5y=0
D) 12x ± y = 0
E) 15x ± 7y = 0
Rpta. : "C"
PREGUNTA 3 :
La ecuación de una hipérbola es 4x² – y² + 2y + 3 = 0 , marcar lo incorrecto
A) Centro: (0; 1)
B) Vértices: (0; 3) y (0; – 1)
C) Focos: (0; 1+√5) y (0; 1–√5)
D) Excentricidad: /2
E) Lado recto: 2
Rpta. : "E"
PREGUNTA 4 :
Hallar la distancia de un foco de la hipérbola 16x² – 9y² = 144 a una cualquiera de sus asíntotas.
A) 3
B) 4
C) 5
D) 6
E) 8
Rpta. : "B"
PREGUNTA 5 :
Determine la longitud del lado recto de una hipérbola de excentricidad 2, si la distancia entre sus directrices es 2.
A) 8
B) 9
C) 10
D) 12
E) 15
Rpta. : "D"
PREGUNTA 6 :
Hallar la ecuación del lugar geométrico de un punto que se mueve de manera que la diferencia numérica de sus distancias a (– 3; 0) y (3; 0) es siempre 4
A) 5x² – 4y² = 20
B) 5y² – 4x² = 20
C) 4y² – 5x² = 20
D) 4x² – 5y² = 20
E) 4x² – y² = 4
Rpta. : "A"
PREGUNTA 7 :
Hallar la ecuación de la hipérbola con vértices en (2; 3), (2; 9) y pasa por (0; 0)
A) 4(x + 2)² – 9(y + 6)² = 36
B) 4(y – 6)² – 27(x – 2)² = 36
C) 9(x – 2)² – 4(y + 6)² = 36
D) 4(y + 2)² – 9(x + 6)² = 36
E) 4(x – 2)² – 27(y – 6)² = 36
Rpta. : "B"
PREGUNTA 8 :
Una hipérbola con centro en el origen tiene un vértice en el punto (– 4; 0) y un foco en el punto (6;0). Según esto, determine la longitud de su lado recto
A) 8
B) 9
C) 10
D) 12
E) 16
Rpta. : "C"
PREGUNTA 9 :
Hallar el centro de la hipérbola:
4y² – 16x² – 48x – 4y+1=0
A) (– 3/2; 1)
B) (– 3/2;1/2 )
C)(– 1/2; 3/2)
D) (3/2; 1/2)
E) (– 3/2; 3/2)
Rpta. : "B"
PREGUNTA 10 :
Hallar la ecuación de la hipérbola cuyos focos son (0;– 2) y (0;2) además cada uno de los lados rectos mide 6
A) x² – y²=1
B) x² –3y²=3
C)2y² –x²=2
D) 3y² –x²=3
E) 3x² – 4y²=12
Rpta. : "D"
PREGUNTA 11 :
Una hipérbola equilátera centrada en el origen pasa por el punto (4; – 1). Hallar la ecuación (posición canónica)
A) x² – 2y²=14
B) x² – y²=15
C) 2y² – x²=14
D) x² – y²=14
E) x² – 2y²=15
Rpta. : "B"
PREGUNTA 12 :
¿Cuál es la ecuación de la hipérbola equilátera centrada en el origen, con vértice en (0;4)?
A) x² – y²=4
B) x² – y²=32
C) y² – x²=4
D) x² – y²=16
E) y² – x²=16
Rpta. : "E"
PREGUNTA 13 :
Dada la hipérbola :
2x² – y²=3 , ¿cuánto mide su eje transverso?
A) 8
B) 3
C) √6
D) √5
E) √3
Rpta. : "C"
PREGUNTA 14 :
¿Cuál es la ecuación de la hipérbola si su centro es C(1;1) y un foco con su vértice correspondiente son (7;1) y (5;1)?
A) 20(x – 1)² – 16(y – 1)²=640
B) 16(y – 1)² – 20(x+1)²=320
C) 5(x – 1)² – 4(y – 1)²=80
D) 16(y – 1)² – 20(x – 1)²=640
E) 20(x – 1)² – 16(y – 1)²=80
Rpta. : "C"
PREGUNTA 15 :
Escríbase la ecuación canónica de la hipérbola si la distancia focal es igual a 10 y la hipérbola pasa por el punto (3;0)
A) 16x² – 9y²=144
B) 9x² – 16y²=144
C) 3x² – 4y²=30
D) 4x² – 5y²=100
E) 16y² – 4x²=35
Rpta. : "A"
PREGUNTA 16 :
La ecuación de una hipérbola es
x² – 4y² – 2x –16y – 19=0
Calcule la distancia entre los focos.
A) 5
B) 2√5
C) 2
D) 4√5
E) 4
Rpta. : "B"
PREGUNTA 17 :
Halle la ecuación de la hipérbola con centro en el origen, una de cuyas asíntotas es la recta 2√5x − 3y = 0 y pasa por el punto P(–1; 2).
A) 10y² – 2x²=2
B) 9y² – 20x²=16
C) 6y² – 3x²=21
D) 9y² – 16x²=20
E) 8y² – 15x²=17
Rpta. : "B"
PREGUNTA 18 :
Dada la ecuación de una hipérbola 9x² – y² –36x–6y +18=0 calcule la ecuación de una de sus rectas asíntotas.
A) y = 3x–3
B) y = 3x– 6
C) y = 3x–9
D) y = 3x– 8
E) y = 3x–12
Rpta. : "C"
PREGUNTA 19 :
Hallar la ecuación de la hipérbola cuyos focos son: (4;– 2) y (4;10), excentricidad es igual a Tg260°
A) 8y² + x² – 64y – 8x + 96 = 0
B) y² – x² + 64y – 6x + 16 = 0
C) 8y² – x² + 8x – 64y + 80 = 0
D) x² – y² – 64y + 6x + 16 = 0
E) 32x² – 4y² – 16x + 8y – 19 = 0
Rpta. : "C"
PREGUNTA 20 :
Calcule el área del triángulo formado por los ejes coordenados y cualquier recta tangente a la hipérbola xy =n; n > 0.
A) 4n
B) n/2
C) n/4
D) 2n
E) n
Rpta. : "D"
PROBLEMAS PROPUESTOS
PREGUNTA 1 :
Halle la ecuación de una hipérbola con centro en el origen, focos sobre el eje Y, lado recto igual a 16/3 y la pendiente de una de sus asíntotas es 3/4 .
A) 4y²–x²=36
B) 4x²–y²=36
C) 16y²–9x²=36
D) 16y²–x²=18
E) 8y²–x²=36
Rpta. : "C"
PREGUNTA 2 :
Calcule el lado recto de una hipérbola cuyas asíntotas tienen por ecuaciones x–y +1= 0, x+ y–3= 0, además uno de los vértices de la hipérbola es (4; 2).
A) 3
B) 4
C) 5
D) 6
E) 8
Rpta. : "D"
PREGUNTA 2 :
Determine la ecuación de la hipérbola con centro en el origen, cuyo eje focal está sobre el eje x, la distancia focal es 6 y la distancia entre las directrices es igual a 4.
A) x² – 2y²=4
B) x² – 3y²=2
C) x² – 4y²=3
D) x² – 2y²=6
E) x² – 9y²=1
Rpta. : "D"
PREGUNTA 3 :
Halle la excentricidad de una hipérbola cuyos extremos del eje transverso son los puntos (1; 6) y (1; 0) y uno de sus focos es (1; 3 – 3√2).
A) 2
B) 3
C) 2
D) 5
E) 3
Rpta. : "A"
PREGUNTA 4 :
Calcule el ángulo obtuso formado por las asíntotas de una hipérbola de excentricidad igual a 2 y eje focal paralelo al eje X.
A) 120°
B) 150°
C) 135°
D) 127°
E) 143°
Rpta. : "A"
PREGUNTA 5 :
Determine la ecuación de la hipérbola que pasa por el punto P(2; 3), tiene su centro en el origen, su eje transverso sobre el eje Y y una de sus asíntotas es la recta ℒ : 2y − 7x = 0.
A) 4y² – 7x²=6
B) 4y² – 7x²=3
C) 4y² – 7x²=2
D) 4y² – 7x²=8
E) 4y² – 7x²=10
Rpta. : "D"
PREGUNTA 6 :
Los focos de una elipse 9y²+25x²–225= 0 coinciden con los focos de una hipérbola. Si la excentricidad es 4/3 , determine la ecuación de la hipérbola.
A) 9x²– 7y²= 1
B) 3y²– 5x²= 45
C) 7y²– 9x²= 1
D) 7y² – 9x²= 63
E) 9y²– 25x²= 225
Rpta. : "D"
PREGUNTA 7 :
Halle la ecuación del lugar geométrico de los puntos de un plano tal que la diferencia de distancias de dichos puntos fijos F1 (2; 4) y F2 (10; 4) es igual a 6.
A) 7x²–9y²–49x+18y +1=0
B) 9x²–7y2+72x–84y +45=0
C) 7x²–9y²–84x+72y +45=0
D) 9x²–7y²+72x–84y +12=0
E) x²–y²–24x+16y +8=0
Rpta. : "C"
PREGUNTA 8 :
Calcule el área de la región triangular limitada por las asíntotas de la hipérbola 9x² −4y² = 36 y la recta 9x+2y–24= 0.
A) 9 u²
B) 12 u²
C) 14 u²
D) 16 u²
E) 18 u²
Rpta. : "B"
PREGUNTA 9 :
Calcule el producto de las longitudes de los radios vectores del punto P(6; 5) de la hipérbola 5x² – 4y²= 80.
A) 60
B) 56
C) 65
D) 36
E) 75
Rpta. : "C"
PREGUNTA 10 :
Dada la hipérbola 4x² – 3y²= 36, calcule la ecuación de la cuerda cuyo punto medio es P(4; 2).
A) 8x – 2y –21=0
B) 8x – 3y – 26=0
C) 7x – 3y – 22=0
D) 6x – 5y –14=0
E) 4x – y –14=0
Rpta. : "B"
PREGUNTA 11 :
Una hipérbola equilátera tiene una asíntota en ℒ : x–y +1= 0 y la otra pasa por (–1; 4) y uno de sus vértices es (4; 2). Halle la ecuación de la hipérbola.
A) x²–y²–2x+4y–12=0
B) y²–x²–4y +2x+12=0
C) x²–y²–2x+4y–16=0
D) y²–x²–4y +2x+16=0
E) x²–y²+2x–2y–4=0
Rpta. : "A"
PREGUNTA 12 :
Calcule el valor de k² para que la recta 2x–y–4= 0 sea tangente a la hipérbola 4x²–k²y²=4k²
A) 1
B) 2
C) 3
D) 4
E) 5
Rpta. : "E"
PREGUNTA 13 :
Las asíntotas de una hipérbola son las rectas x+2y = 4, x–2y = 0 y un foco es el punto (2; 5). Calcule la distancia entre sus directrices.
A) 8/5
B) 9/5
C) 7/2
D) 4/3
E) 6/5
Rpta. : "A"
PREGUNTA 14 :
Halle la ecuación de la hipérbola con foco F(3;3), directriz ℒ : x+3y – 3=0 y excentricidad e=2.
A) 3x² – 12xy – 13y² – 18x+6y +72=0
B) 3x² –12xy – 13y² – 18x+36y +70=0
C) 3x² – 10xy – 13y² – 18x+36y +72=0
D) 3x² – 12xy – 14y² –18x+33y +62=0
E) 2x² – 5xy +13y² – 17x+35y – 60=0
Rpta. : "A"
PREGUNTA 15 :
Si e1 es la excentricidad de la hipérbola
3x²–5y²+6x+10y–17=0 y e2 es la excentricidad de su conjugada.
Calcule 15e1e2.
A) 2
B) 4
C) 8
D) 6
E) 10
Rpta. : "C"
APRENDIZAJES ESPERADOS
• Entender la ecuación de la hipérbola y sus elementos.
• Aprender a hallar la ecuación general de una hipérbola .
• Conocer la ecuación ordinaria de la hipérbola
La hipérbola es una curva resultado de la intersección de un cono con un plano paralelo al eje del cono.
Si usas una linterna (cuyo haz de luz es cónico) y la colocas paralela a una pared, el borde de luz que se ve contra la pared es una perfecta hipérbola.
DEFINICIÓN :
La hipérbola es el lugar geométrico de los puntos de tal manera que si tomamos un punto cualquiera de la curva , la diferencia de sus distancias a los focos es igual a 2a .
Dado dos puntos fijos distintos F1 y F2 denominados focos.
Se define la hipérbola como el lugar geométrico del conjunto de puntos P(x ; y) tales que la diferencia de sus distancias a los puntos fijos F1 y F2 en valor absoluto es igual a una constante convencional 2a.
Según la definición, sea F1 y F2 los puntos fijos denominados focos y P(x;y) un punto cualquiera de la hipérbola respectivamente, luego:
|d(P; F1) – d (P; F2)| = 2a
ELEMENTOS :
CUERDA
Es un segmento que une dos puntos de la curva .
CUERDA FOCAL
Es una cuerda que pasa por el foco
LADO RECTO
Es una cuerda focal perpendicular al eje transverso .
RADIO VECTOR
Es el segmento que une el foco con un punto cualquiera de la hipérbola .
P(x;y) : punto P de coordenadas genéricas (x;y) pertenecientes a la hipérbola.
Los Ejes focal y normal son los ejes de simetría de la hipérbola.
DIRECTRICES
son las rectas perpendiculares al eje transverso
Los ejes focal y normal , son sus respectivos ejes de simetría de la hipérbola. a; b; c son números positivos por ser longitudes.
En cualquier hipérbola siempre se cumple que una circunferencia pasa por los focos y por los vértices del «Rectángulo fundamental de la hipérbola MNWQ», siendo el centro de la hipérbola el centro de la circunferencia.
Toda hipérbola es simétrica con respecto a sus ejes de simetría , es decir con respecto a su eje transverso y con respecto al eje conjugado.
Si se traza una cuerda perpendicular al eje de simetría , la cuerda quedará dividida en dos partes iguales.
EXCENTRICIDAD DE UNA HIPÉRBOLA (e)
Es un elemento importante de una hipérbola que se denota por e . Saber el valor de e nos permite identificar la cónica .
ECUACIONES DE LA HIPÉRBOLA
La ecuación cartesiana de la hipérbola para todo punto P de coordenadas genéricas (x;y), depende de la ubicación del eje focal respecto a los ejes coordenados.
A continuación, se analizan las diversas ecuaciones.
I) PRIMERA FORMA (CANÓNICA) :
Es cuando la hipérbola tiene su centro en el origen (0;0) y su eje transverso está en el eje X .
II) SEGUNDA FORMA (CANÓNICA) :
Es cuando la hipérbola tiene su centro en el origen (0;0) y su eje transverso está en el eje Y .
III) TERCERA FORMA (ORDINARIA) :
Es cuando la hipérbola tiene su centro en el punto C(h;k) y su eje transverso es paralelo al eje X .
IV) CUARTA FORMA (ORDINARIA)
Es cuando la hipérbola tiene su centro en el punto C(h; k) y su eje transverso es paralelo al eje Y .
ECUACIÓN GENERAL DE UNA HIPÉRBOLA
Una Ecuación de segundo grado que carece del término rectangular xy , es de la forman : Ax²+Cy²+Dx+Ey+F=0
Para que esta ecuación de segundo grado sea una hipérbola A y C deben ser de signos contrarios.
La Ecuación general de la hipérbola : Ax²+Cy²+ Dx+Ey+F=0
Se puede reducir a la forma ordinaria de la hipérbola
Ecuación ordinaria de una hipérbola :
I) Si t > 0, se trata de una hipérbola horizontal canónica u ordinaria .
II) Si t < 0, se trata de una hipérbola vertical canónica u ordinaria .
III) Si t=0, se trata de dos rectas que se intersectan.
ASÍNTOTAS DE UNA HIPÉRBOLA
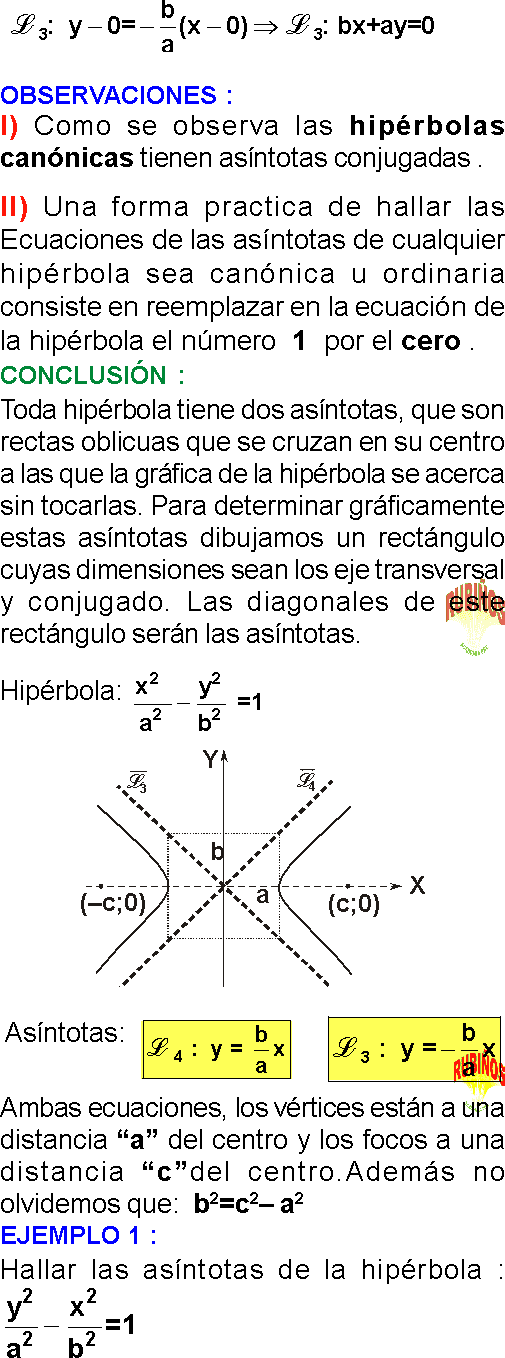
I) Como se observa las hipérbolas canónicas tienen asíntotas conjugadas .
II) Una forma practica de hallar las Ecuaciones de las asíntotas de cualquier hipérbola sea canónica u ordinaria consiste en reemplazar en la ecuación de la hipérbola el número 1 por el cero .
CONCLUSIÓN :
Toda hipérbola tiene dos asíntotas, que son rectas oblicuas que se cruzan en su centro a las que la gráfica de la hipérbola se acerca sin tocarlas.
Para determinar gráficamente estas asíntotas dibujamos un rectángulo cuyas dimensiones sean los eje transversal y conjugado.
Las diagonales de este rectángulo serán las asíntotas.
TANGENTES A UNA HIPÉRBOLA
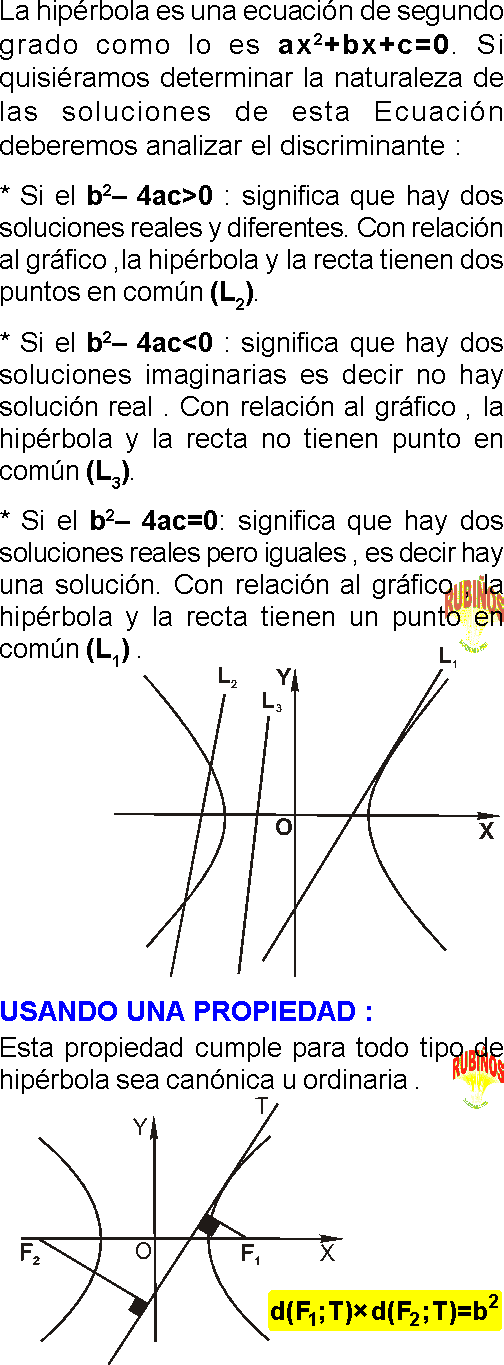
Usaremos el método del discriminante que sirve para resolver problemas sobre tangente a cualquier cónica , es un método general.
USANDO UNA PROPIEDAD :
Esta propiedad cumple para todo tipo de hipérbola sea canónica u ordinaria .
El producto de la distancia de los focos de una hipérbola a una misma recta tangente es igual a b²
b= semieje conjugado
Como la ecuación de una hipérbola es de segundo grado , sus tangentes pueden obtenerse empleando la condición de tangencia o el método empleado para hallar la ecuación de la tangente a una elipse .
TANGENTE EN UN PUNTO DE CONTACTO :
TANGENTE DE PENDIENTE DADA
HIPÉRBOLAS CONJUGADAS
Dos hipérbolas son conjugadas cuando el eje transverso de cada una es igual al eje conjugado de la otra .
Son hipérbolas conjugadas HIPÉRBOLA EQUILÁTERA O RECTANGULAR
Se denomina así porque sus ejes transverso y conjugado tienen igual longitud , es decir a=b .
EXCENTRICIDAD DE UNA HIPÉRBOLA EQUILÁTERA
CASOS ESPECIALES DE HIPÉRBOLAS EQUILÁTERAS O RECTANGULARES
CUERDA DE CONTACTO
Si desde un punto exterior P1 se trazan tangentes a una hipérbola , el segmento de recta que une los puntos de contactos se llama cuerda de contacto de P1 para dicha hipérbola.
ECUACIÓN DE DIÁMETRO DE UNA HIPÉRBOLA
Se denomina diámetro de una hipérbola al lugar geométrico de los puntos medios de cualquier sistema de cuerdas paralelas .
DIÁMETROS CONJUGADOS
Si dos diámetros son tales que cada uno de ellos biseca a las cuerdas paralelas del otro , se les llama Diámetros Conjugados.
En la hipérbola la ecuación del diámetro que biseca a las cuerdas de pendiente ‘‘m’’ es Entonces la ecuación de su conjugada es : y=mx .
PROPIEDAD INTRÍNSECA DE LA HIPÉRBOLA
TEOREMAS SOBRE LA HIPÉRBOLA
TEOREMA 1 :
La tangente a una hipérbola en cualquier punto P es bisectriz del ángulo formado por los radios focales correspondientes a dicho punto .
TEOREMA 2 :
La normal a una hipérbola es bisectriz del ángulo formado por uno de los radios focales correspondientes al punto de contacto y la prolongación del otro .
TEOREMA 3 :
En toda hipérbola de eje transverso horizontal , las tangentes en los extremos de los lados rectos tienen pendientes que son numéricamente iguales a la excentricidad , esto es :
TEOREMA 4 :
El producto de las distancias de los focos de una hipérbola a cualquier tangente es constante e igual al cuadrado de la longitud del semieje conjugado , esto es :
TEOREMA 5 :
La distancia de un foco de una hipérbola a cualquiera de sus asíntotas es igual a la longitud de su semieje conjugado
TEOREMA 6 :
El producto de las distancias de cualquier punto de una hipérbola a sus asíntotas es constante.
TEOREMA 7 :
Si las asíntotas de una hipérbola son perpendiculares entre sí , la hipérbola es equilátera. .