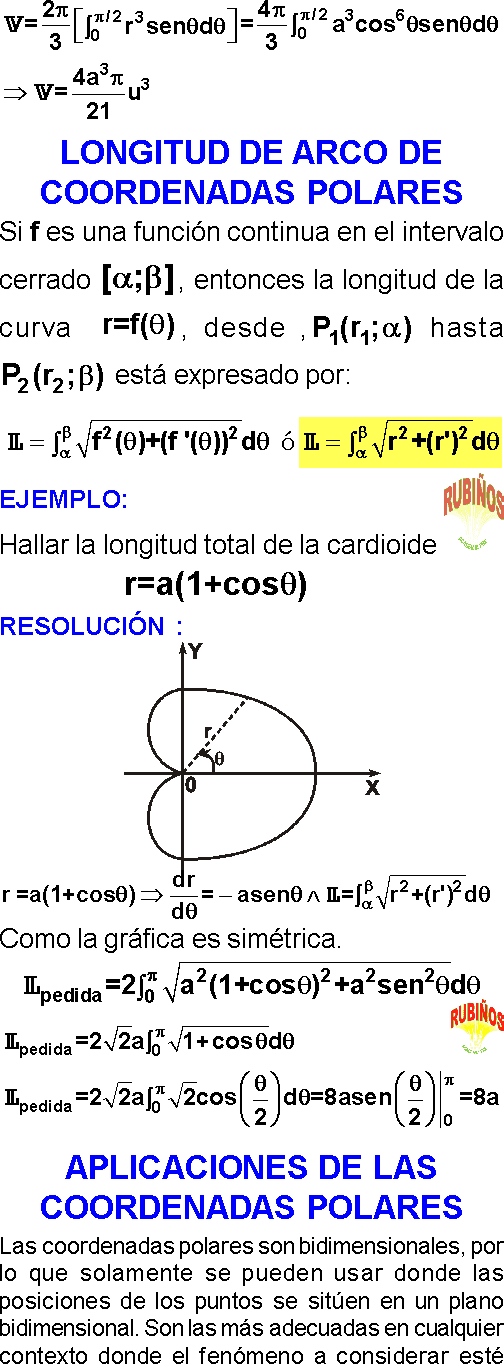COORDENADAS POLARES EJERCICIOS RESUELTOS PDF
APRENDIZAJES ESPERADOS
• Identificar los elementos de la representación en coordenadas polares : polo, eje polar, ángulo, radio vector.
• Definir las coordenadas polares y la relación que se da con las coordenadas rectangulares.
• Expresar las ecuaciones y gráficas de las cónicas con coordenadas polares.
• Aplicar la teoría en los diversos problemas de examen de admisión
¿Por qué se estudian diferentes sistemas de coordenadas?
Porque ciertas curvas se describen de manera más natural en un sistema coordenado que en otro.
En coordenadas rectangulares se pueden dar ecuaciones simples para líneas, parábolas, pero la ecuación de un círculo es bastante complicada.
En coordenadas polares, se pueden dar ecuaciones simples para círculos, elipses, curvas que es difícil describir en coordenadas rectangulares.
GUIA DE CLASE
EJERCICIO 1 :
Transformar el punto (– 6 ;7𝛑/4) en sus coordenadas cartesianas.
EJERCICIO 2 :
Hallar las coordenadas cartesianas de P , si sus coordenadas polares son (3;2𝛑/3)
EJERCICIO 3 :
Determine las coordenadas rectangulares del punto P , cuyas coordenadas polares son (4;3𝛑/4)
EJERCICIO 4 :
Determine las coordenadas rectangulares del punto P, cuyas coordenadas polares son (2;2𝛑/3)
EJERCICIO 5 :
Halle un conjunto de coordenadas polares para P
Si sus coordenadas cartesianas son (2 ; –2)
EJERCICIO 6 :
Transformar la ecuación r²𝑐𝑜𝑠2𝜃=9 a coordenadas cartesianas
EJERCICIO 7 :
Transformar la ecuación x²+y²=4x a coordenadas polares.
EJERCICIO 8 :
Determine la ecuación polar del lugar geométrico cuya ecuación rectangular es:
(x – 2)² + (y –2)²= 4
EJERCICIO 9 :
Determine la ecuación polar del lugar geométrico cuya ecuación rectangular es:
x² – y²=4
EJERCICIO 10 :
Encontrar una ecuación polar de la gráfica cuya ecuación cartesiana es dada por:
x² + y²=a²
EJERCICIO 11 :
Encontrar una ecuación polar de la gráfica cuya ecuación cartesiana es :
y²=4(x+1)
EJERCICIO 12 :
Dada la ecuación rectangular del lugar geométrico x² = 4y exprese la misma en forma polar.
EJERCICIO 13 :
Determine la ecuación polar del lugar geométrico cuya ecuación cartesiana es:
x² – y² = 2
EJERCICIO 14 :
Hallar la ecuación de la recta sabiendo que pasa por el punto(4;𝛑/6) y forma un ángulo de 5𝛑/6 con el eje polar.
EJERCICIO 15 :
Halle la ecuación polar de la circunferencia de centro (3;𝛑/6) y radio 8.
EJERCICIO 16 :
Calcule la ecuación polar de la elipse cuya ecuación cartesiana es
9x² + 4y² – 36= 0
EJERCICIO 17 :
Una elipse tiene un foco en el polo con centro C(4;𝛑) y vértice V(2; 0).
Encuentre una ecuación polar para la elipse.
EJERCICIO 18 :
La ecuación cartesiana de una curva es x³+ y³=2kxy
Determine la ecuación polar de dicha curva.
EJERCICIO 19 :
Halle la ecuación polar del lugar geométrico, cuya ecuación rectangular es
(x – 2)² + (y – 2)²=4
EJERCICIO 20 :
Obtenga la ecuación polar de la curva que tiene por ecuación cartesiana
4x² – 5y² – 36y – 36=0
EJERCICIO 21 :
Calcule el área de la región limitada por los ejes coordenados en el primer cuadrante y la curva cuya ecuación polar es r =senθ +cosθ.
EJERCICIO 22 :
Graficar el siguiente cardioide:
r=1+𝑐𝑜𝑠𝜃
EJERCICIO 23 :
Graficar : r=1 – 2𝑐𝑜𝑠𝜃
POSICIÓN DE UN PUNTO EN COORDENADAS POLARES
En un sistema de coordenadas polares un punto P del plano se representa por un par de números , donde r es la distancia del origen (llamado polo) al punto dado:
EJEMPLO
En coordenadas polares, el punto es ubicado dibujando primero un rayo que parte del polo (origen) que haga un ángulo rad.
RELACIÓN ENTRE LAS COORDENADAS RECTANGULARES Y LAS POLARES
Sea O(0;0) el polo y el eje polar de un sistema de coordenadas polares y al mismo tiempo sean el origen de un sistema de coordenadas rectangulares.
Sea un punto cualquiera del plano, (x;y) sus coordenadas rectangulares, y sus coordenadas polares.
DISTANCIA ENTRE DOS PUNTOS EN COORDENADAS POLARES
TRAZADO DE CURVAS EN COORDENADAS POLARES
La gráfica ó lugar geométrico de una ecuación expresada en coordenadas polares es:
ECUACIÓN DE LA RECTA
I) LA RECTA L NO PASA POR EL ORIGEN (POLO)
II) CUANDO LA RECTA L PASA POR EL ORIGEN (POLO)
ECUACIÓN DE UNA CIRCUNFERENCIA
La ecuación polar de una circunferencia con centro en y radio a>0 es
ECUACIÓN DE UNA CIRCUNFERENCIA QUE PASA POR EL POLO
EJEMPLO:
Grafique r=5
ECUACION POLAR GENERAL DE UNA CONICA
Cuando el eje de las abcisas es un eje de la cónica y el eje de las ordenadas es una directriz resulta (x–d)²+y²=e².x² , donde e representa la excentricidad y d la distancia a la directriz correspondiente.
Podemos efectuar un cambio de ejes coordenados a unos nuevos ejes que tengan el foco de la cónica como origen y el eje de la cónica como eje de las abcisas haciendo x=d+x’ ; y=y’
EN GENERAL :
Sea e la excentricidad de una cónica cuyo foco está en el polo y a d unidades de la directriz correspondiente.
* Si el eje focal coincide con el eje polar , la ecuación de la cónica es de la siguiente forma :
* Si el eje focal coincide con el eje normal , la ecuación de la cónica es de la siguiente forma :
Si e=1 resulta una parábola
Si e<1 resulta una hipérbola
DISCUCIÓN DE UNA ECUACIÓN POLAR
Para facilitar el trazado de la gráfica de una ecuación en coordenadas polares es conveniente establecer el siguiente análisis.
I) SIMETRÍA :
A) La curva es simétrica con respecto al eje polar si se obtiene una ecuación equivalente ( que no varía ) cuando se sustituye
B) La curva será simétrica con respecto al eje 𝛑/2 si se obtiene una ecuación equivalente cuando se sustituye
C) La curva será simétrica con respecto al polo si se obtiene una ecuación equivalente ( que no varía ) cuando se sustituye
II) INTERCEPTOS CON LOS EJES PRINCIPALES
III) EXTENSIÓN :
IV) TABULACIÓN :
Se determina los valores de r correspondientes a algunos valores asignados a 𝜃.
Luego se localizan los puntos obtenidos y se traza la curva.
RECTAS TANGENTES EN EL POLO
SIMETRÍAS
INTERCEPTOS
RECTAS TANGENTES EN EL POLO:
CARDIOIDE
La gráfica polar de la ecuaciones: se les llama limazón; palabra francesa que proviene del latín Limax que significa caracol.
TIPOS DE CARACOLES: SIMETRÍA Y DIRECCIÓN DE UN CARACOL :
EJERCICIO
Gráficar la ecuación polar siguiente (lemniscata).
INTERSECCIÓN DE GRÁFICAS EN COORDENADAS POLARES
Cuando teníamos dos gráficas determinadas por ecuaciones cartesianas en las variables x, y , para hallar todos los puntos de intersección de sus gráficas simplemente resolvíamos ambas ecuaciones simultáneamente.
Sin embargo, cuando se trata de dos gráficas descritas por ecuaciones en coordenadas polares r ,𝜃 , esta técnica no proporciona necesariamente todos los puntos de intersección de ambas gráficas. Los siguientes dos ejemplos ilustrarán este hecho.
DERIVADAS Y RECTAS TANGENTES EN COORDENADAS POLARES
ÁREA DE UNA REGIÓN EN COORDENADAS POLARES :
Antes de pasar a las aplicaciones aconsejamos al estudiante revisar los criterios para gráficar e intersecar curvas polares, como interceptos, simetrías, rectas tangentes en el polo.
VOLUMEN DE UN SÓLIDO DE REVOLUCIÓN EN COORDENADAS POLARES
LONGITUD DE ARCO DE COORDENADAS POLARES
EJEMPLO:
Hallar la longitud total de la cardioide
APLICACIONES DE LAS COORDENADAS POLARES
Las coordenadas polares son bidimensionales, por lo que solamente se pueden usar donde las posiciones de los puntos se sitúen en un plano bidimensional.
Son las más adecuadas en cualquier contexto donde el fenómeno a considerar esté directamente ligado con la dirección y longitud de un punto central, como en las figuras de revolución, en los movimientos giratorios, en las observaciones estelares, etc.
Los ejemplos vistos anteriormente muestran la facilidad con la que las coordenadas polares definen curvas como la espiral de Arquímedes, cuya ecuación en coordenadas cartesianas sería mucho más intrincada.
Además muchos sistemas físicos, tales como los relacionados con cuerpos que se mueven alrededor de un punto central, o los fenómenos originados desde un punto central, son más simples y más intuitivos de modelar usando coordenadas polares.
La motivación inicial de la introducción del sistema polar fue el estudio del movimiento circular y el movimiento orbital.
POSICIÓN Y NAVEGACIÓN :
Las coordenadas polares se usan a menudo en navegación, ya que el destino o la dirección del trayecto pueden venir dados por un ángulo y una distancia al objeto considerado. Las aeronaves, por ejemplo, utilizan un sistema de coordenadas polares ligeramente modificado para la navegación.
MODELADO :
Los sistemas que presentan simetría radial poseen unas características adecuadas para el sistema de coordenadas polares, con el punto central actuando como polo. Un primer ejemplo de este uso es la ecuación del flujo de las aguas subterráneas cuando se aplica a pozos radialmente simétricos.
De la misma manera, los sistemas influenciados por una fuerza central son también buenos candidatos para el uso de las coordenadas polares.
Citemos por ejemplo las antenas radioeléctricas, o los campos gravitatorios, que obedecen a la ley de la inversa del cuadrado (véase el problema de los dos cuerpos).
Los sistemas radialmente asimétricos también pueden modelarse con coordenadas polares. Por ejemplo la directividad de un micrófono, que caracteriza la sensibilidad del micrófono en función de la dirección del sonido recibido, puede representarse por curvas polares.
La curva de un micrófono cardioide estándar, el más común de los micrófonos, tiene por ecuación r = 0,5 + 0,5sen𝜃