PLANO CARTESIANO EJERCICIOS RESUELTOS PDF
El plano cartesiano es un sistema de coordenadas bidimensional que permite ubicar puntos, líneas y figuras en un espacio. Fue ideado por el matemático y filósofo francés René Descartes.
USOS:
• En matemáticas para graficar funciones o resolver sistemas de ecuaciones.
• En física para representar vectores y movimientos.
• En estadística para analizar relaciones entre variables.
PROBLEMAS RESUELTOS
PREGUNTA 1 :
Hallar la distancia entre los puntos, cuyas coordenadas son: (0;3) y (– 4 ; 1).
A) 2√3
B) 2√5
C) 3
D) 5
E) 3√2
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 2 :
Un triángulo ABC tiene por coordenadas A(– 5 ; 1) , B(– 5 ; 4) y C( 2 ; 4).
Calcular el área del triángulo.
A) 10,5 u²
B) 12,5 u²
C) 14,5 u²
D) 16 u²
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 3 :
Si A(1;3) y B(2;–5) son los puntos extremos del segmento AB, halle la suma de las coordenadas del punto de trisección más próximo al extremo A.
A) –1/3
B) 5/3
C) –2/3
D) –5/3
E) 2/3
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 4 :
Si ABCD es un paralelogramo, determine las coordenadas de D.
A) (–7;–3)
B) (–3;2)
C) (–7;3)
D) (–6;2)
E) (–5;1)
RESOLUCIÓN :
Rpta. : "C"
SISTEMA UNIDIMENSIONAL
Los números reales se pueden ubicar en una recta numérica por convención los números positivos se ubican a la derecha del cero (0) y los números negativos a la izquierda de este. Debido a la gran densidad de los números reales, estos pueden estar ubicados en la recta numérica.
Existiendo una relación biunívoca entre los números reales y cada punto de la recta; es decir, a cada punto de la recta le corresponde un sólo número real, asimismo a cada número real le corresponde un punto de la recta.
SISTEMA BIDIMENSIONAL
A partir del concepto de un sistema unidimensional se puede establecer una correspondencia biunívoca entre los puntos de un plano y pares ordenados de números reales.
Lo cual permite denominar lo que es el PLANO CARTESIANO que es un sistema formado por dos rectas numéricas las cuales se cortan perpendicularmente en sus orígenes y dicha intersección será el origen de coordenadas.
A la recta HORIZONTAL se le conoce como EJE DE ABCISAS (X), mientras que a la recta VERTICAL se le denomina EJE DE ORDENADAS (Y).
En un plano se trazan dos rectas perpendiculares, la recta horizontal se denomina eje X y la recta vertical se llama eje Y en ambas rectas el real cero, es llamado el origen.
Al plano y a las rectas reales trazadas en él se denominan Plano cartesiano o plano coordenado. Se elige la dirección hacia la derecha en el eje X y la dirección hacia arriba en el eje Y como positivas.
Si P es un punto del plano, al trazar una recta perpendicular al eje horizontal que pasa por el punto, se determina un único punto en el eje X, al que corresponde un único número real x ; de igual forma, si se traza una perpendicular por P al eje vertical se determina un único punto en el eje Y al cual corresponde un único número real y. Así, a cada punto del plano se asocia una pareja ordenada de números reales x, y llamadas coordenadas de P.
La coordenada X o abscisa del punto corresponde a la distancia de P al eje Y y la coordenada Y u ordenada de P a la distancia de P al eje X. Un punto cuya abscisa es X y cuya ordenada es Y se designa (x ; y) en este orden, primero la abscisa y luego la ordenada.
Las coordenadas de un punto son un par ordenado de números reales; se acostumbra referirse a las coordenadas del punto como si ellas fueran el punto.
Si P es un punto del plano cartesiano, entonces a “P” le corresponde una pareja de números (x;y) llamados las coordenadas de P.
UBICACIÓN DE UN PUNTO
La ubicación de un punto en el plano cartesiano se representa mediante un par ordenado (x;y) ; en donde a este punto se conoce como “Coordenadas del Punto”.
RADIO VECTOR (r)
A la distancia de un punto del plano cartesiano al origen se llama RADIO VECTOR (r) y se le considera positivo.
EJEMPLO 1 :
Halle el radio vector para el punto: (8 ; 15), (– 3 ; 4), (– 5 ; – 4) y (–7 ; 24)
EJEMPLO 2 :
Calcular el radio vector para el punto (–3 ; 4)
EJEMPLO 3 :
Hallar el radio vector para el punto (3 ; –2)
DISTANCIA ENTRE DOS PUNTOS(Sistema Bidimensional)
EJEMPLO 4 :
Hallar la distancia entre los puntos: A(3 ; 2) y B(8 ; 5).
EJEMPLO 5 :
Hallar la distancia entre los puntos A(3 ; 7) y B (–2 ; 4)
EJEMPLO 6 :
Calcular la distancia entre los puntos P1(–3 ; 2) y P2(12 ;– 6)
DIVISIÓN DE UN SEGMENTO EN UNA RAZÓN DADA PUNTO MEDIO DE UN SEGMENTO
EJEMPLO 7 :
Calcule las coordenadas del punto medio M(x ; y) del segmento cuyos extremos son: (– 4 ; 12) y (6 ; – 6)
EJEMPLO 8 :
Hallar el punto medio del segmento que une a los puntos A(3 ; 8) y B(13 ; 12)
COORDENADAS DEL BARICENTRO DE UN TRIANGULO
EJEMPLO 9 :
Calcular las coordenadas del baricentro de un triángulo cuyos vértices son: A (1 ; 2), B (5 ; 8) y C(9 ; 5).
EJEMPLO 10 :
Calcule las coordenadas del baricentro de un triángulo cuyos vértices son A(–3 ; 4); B(4 ; 8) y C(–6 ; –3).
ÁREA DE UNA REGIÓN TRIANGULAR
EJEMPLO 11 :
Los vértices de un triángulo son A(–2 ; 5); B(3 ; 7) y C(6 ; –3). Calcule su área.
ÁREA DE UN POLÍGONO DE “n” VÉRTICES
EJEMPLO 12 :
Hallar el área del cuadrilátero que tiene los vértices consecutivos :
A(3 ; 5) ; B(2 ; 1) ; C(8 ; 3) ; D(7 ; 7)
PRIMERA PRACTICA
PREGUNTA 1 :
Calcular la distancia entre los puntos A(–3;4) y B(5; – 2)
A) 10 u
B) 11
C) 12
D) 13
E)14
Rpta. : "A"
PREGUNTA 2 :
(3;–1) es el punto medio de un segmento donde uno de sus extremos es el punto (1;2). Hallar las coordenadas de otro extremo.
A) (5; – 4)
B) (5; 4)
C) (– 4;5)
D) (1; 1/2)
Rpta. : "A"
PREGUNTA 3 :
Dado los puntos A(–4; 3); B(–4;–13) y C(4;2) forman un triángulo al unir los puntos. Calcular su perímetro.
A) 30u
B) 24
C) 42
D) 30
E) 40
Rpta. : "E"
PREGUNTA 4 :
El segmento que une A(–2;–1) con B(2;2) se prolonga hasta C. Si BC=3AB. Halle las coordenadas de C.
A) (6;12)
B) (10;14)
C) (12;8)
D) (14;11)
E) (10;12)
Rpta. : "D"
PREGUNTA 5 :
Si las coordenadas del punto medio del segmento AB es (–2;1), calcular las coordenadas del punto B si A tiene como coordenadas (8; 12)
A) (11; 11)
B) (11; 12)
C) (–12; –10)
D) (–13; –12)
E) (–14; –11)
Rpta. : "C"
PREGUNTA 6 :
En el triángulo dos de sus vértices son A(1;3) y B(7;1), además su baricentro es G(5;0).¿Cuál es la suma de coordenadas del tercer vértice “C”?.
A) 3
B) 5
C) 1
D) 0
E) 2
Rpta. : "A"
PREGUNTA 7 :
Calcular la distancia máxima del punto P(11;12) exterior a una circunferencia de centro (3;6) y su radio mide 3cm.
A) 10cm.
B) 11
C) 12
D) 13
E) 14
Rpta. : "D"
PREGUNTA 8 :
Hallar la altura del triángulo ABC, relativa al lado AB, si A(– 2;5); B(– 2;8); C(6;3)
A) 8
B) 7
C) 6
D) 5
E) 4
Rpta. : "A"
PREGUNTA 9 :
En un triángulo rectángulo ABC (recto en B), A(1;1) y C(6;11). El cateto BC mide 5. Calcule la suma de las coordenadas del punto B.
A) 16
B) 15
C) 14
D) 17
E) 13
Rpta. : "A"
PREGUNTA 10 :
Si dos vértices opuestos de un paralelogramo son: A(1;1) y C=(3;5), ¿cuál es el punto de corte de las diagonales?
A) (2;4)
B) (2;3)
C) (1;3)
D) (2;2)
E) (3;3)
Rpta. : "B"
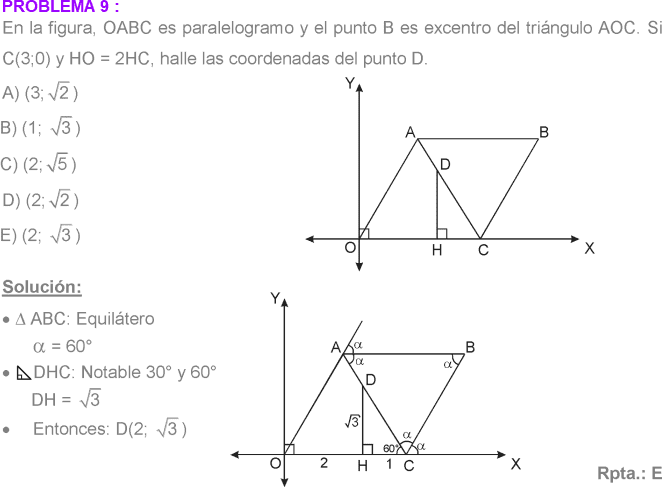
PREGUNTA 11 :
Sea el paralelogramo ABCD tal que : A(3;–4), B(6;5) y C(–3 ; –2), entonces las coordenadas de vértices D es:
A) (– 6 ; – 10)
B) (– 6; –11)
C) (– 5; –11)
D) (– 5 ; – 12)
E) (– 6; –14)
Rpta. : "B"
PREGUNTA 12 :
Si los vértices de un triángulo son: A=(1;4); B =(3; – 9); C=(– 5;2)
Determine la longitud de la mediana trazada desde el punto “B”.
A)11
B) 12
C) 13
D)15
E) 17
Rpta. : "C"
PREGUNTA 13 :
Si los puntos (1 ; 6) y (5 ; 2) son los vértices opuestos de un cuadrado , entonces el área del cuadrado es:
A) 32
B) 50
C) 4
D)16
E) 8
Rpta. : "D"
PREGUNTA 14 :
Las coordenadas de los vértices de un triángulo son: A(–1;1), B(3;7) y C(5;–3). Calcular la longitud de la altura relativa al lado BC.
A) 5
B) 4
C) √26
D)√15
E) √17
Rpta. : "C"
PREGUNTA 15 :
Con los puntos medios de los lados del triángulo cuyos vértices son A(– 2;4), B(6;8) y C(4; – 6) se construye un triángulo, calcular su área.
A) 13m²
B) 12
C) 20
D) 16,5
E) 14,6
Rpta. : "A"
PREGUNTA 16 :
Halle la ecuación de la curva tal que la distancia de cualquier punto de ella al origen de coordenadas y al punto F=(6;0) están en la relación de 2 a 1.
A) x² + 8y² = 16
B) x² + y² = 8
C) x² – y² = 2
D) x – 3y = 1
E) (x – 8)² + y² = 16
Rpta. : "E"
PREGUNTA 17 :
Si A(– 3;4), B(4;5) y C(1; – 4) son vértices de un triángulo, encontrar las coordenadas del circuncentro del triángulo.
A) (1;1)
B) 1;–1)
C) (2;–1)
D) (–3;-1)
Rpta. : "A"
PREGUNTA 18 :
La base mayor de un trapecio isósceles une los puntos (– 2;8) y (– 2; – 4). Uno de los extremos de la base menor tiene por coordenada (3;–2). La distancia o longitud de la base menor es:
A) 8
B) 6
C) 9
D) 12
E) 10
Rpta. : "A"
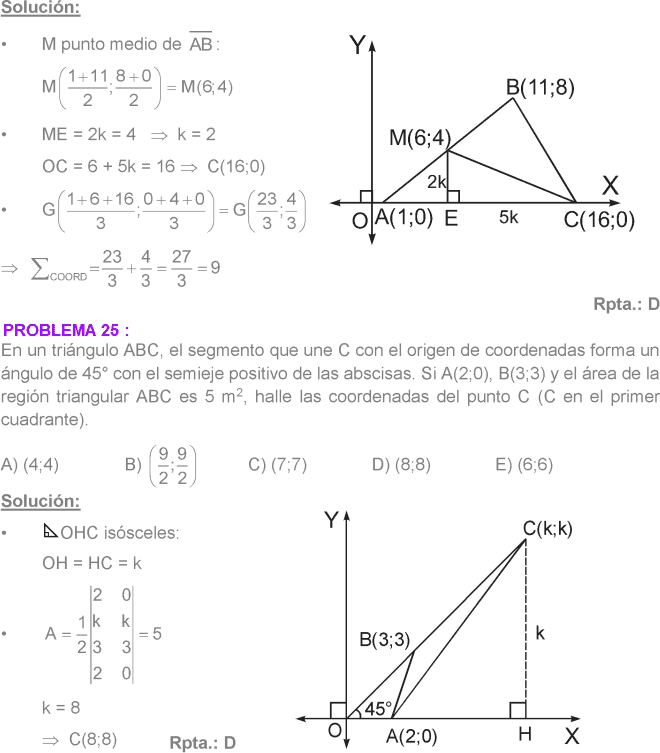
PREGUNTA 19 :
A(3;1), B(1;– 3) son las coordenadas de dos vértices de un triángulo de 3m2 de área, si el baricentro pertenece al eje de las abscisas. Halle la suma de las coordenadas del vértice C.
A) 7 ó 4
B) 6 ó 5
C) 3 ó 8
D) 2 ó 9
E) 1 ó 10
Rpta. : "A"
PREGUNTA 20 :
El punto P=(h+2k; h–k) divide al segmento AB en la razón 1/3.
Si A=(–2; 2) y B = (h – k; 2k – 2k), calcule h y k .
A) 3/2 y – 3/2
B) 4/7 y 4/9
C) 7/4 y – 5/4
D) 7/6 y – 5/4
E) 7/5 y – 6/7
Rpta. : "C"
PREGUNTA 21 :
El punto M divide a BA internamente en la razón 1/4.
Si M=(– 3;5) y B=(2;2), calcule la suma de componentes de A .
A) – 6
B) 6
C) 5
D) – 5
E) 7
Rpta. : "A"
PREGUNTA 22 :
Edu asocia el plano de su localidad con un sistema de coordenadas. Si su casa está ubicada en el punto C( – 6; 8), el mercado está en el punto M( – 3; – 3) y el banco en el punto B(4; 2). ¿Cuál es la longitud aproximada del recorrido que realiza Edu si primero va al banco, luego al mercado y finalmente a su casa?
A) 31,6 u
B) 28,4 u
C) 30,8 u
D) 32,8 u
Rpta. : "A"
PREGUNTA 23 :
Un pueblo A(2; 3) equidista de dos pueblos P(5; –1) y Q(a ; 0). Halle un posible valor de a.
A) 2
B) 3
C) 4
D) 6
Rpta. : "D"
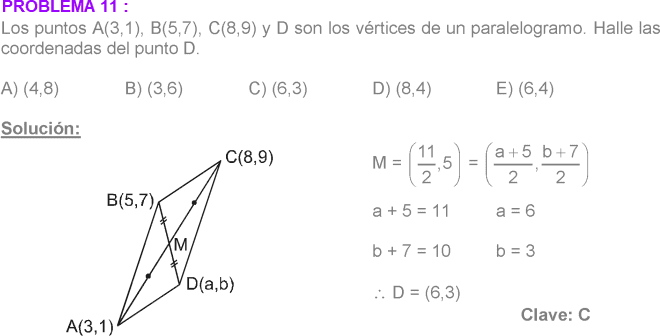
PREGUNTA 24 :
Los puntos A(3; 1), B(5; 7), C(8; 9) y D(a; b) son vértices de un paralelogramo. Calcule la distancia del vértice D al punto medio de AB.
A) 5
B) √5
C) 4
D) √3
Rpta. : "B"
APRENDIZAJES ESPERADOS
• Ubicar los puntos en el eje de coordenadas
• Reconocer la abcisa y ordenada en el eje de coordenadas
• Determinar puntos en un sistema bidimensional de coordenadas que corresponden a pares ordenados de números reales.
• Establecer la noción de plano y en él ubicar formas geométricas que se forman con los puntos.
• Reconocer puntos en un sistema bidimensional que correspondan a una forma geométrica conocida.
• Reconocer y aplicar fórmulas básicas del cálculo de una distancia entre dos puntos.
• Calcular las coordenadas del baricentro de un triángulo.
• Reconocer y aplicar fórmula para el cálculo de las coordenadas del punto medio y división de un segmento en una razón dada.
Los términos PLANO, RECTA y PUNTO, no son posibles de definir.
Se acepta en cambio que entre punto, recta y plano existen ciertas relaciones.
Algunas de éstas relaciones son:
I) Las rectas y los planos son conjuntos de puntos.
II) Por dos puntos pasa una única recta.
III) Cuando se tienen tres puntos en una recta, exactamente uno de ellos está entre los otros dos.
IV) Dos rectas distintas tienen a lo más un punto en común
