LÓGICA PROPOSICIONAL EJERCICIOS RESUELTOS PDF

Frecuentemente los términos «lógico» e «ilógico» los utilizamos para indicar lo que es razonable en contraposición de lo que no es razonable. 
Evidentemente que estos términos tienen que ver con la lógica. 
Pero ¿ qué es la lógica? 
No trataremos de definir a la lógica porque de hacerlo. sería circunscribir su dominio o campo de aplicación. 
Simplemente diremos que la lógica se ocupa de examinar los diversos procedimientos teóricos y experimentales que se utilizan en la adquisición de conocimientos. 

Por lo tanto la lógica estudia los procesos del pensamiento para descubrir los elementos racionales que la constituyen y las funciones que los enlazan. Igualmente la lógica indaga las relaciones mutuas y las influencias recíprocas que existen entre el pensamiento y la realidad representada por este pensamiento. 
¿Por qué es necesario estudiar lógica? 
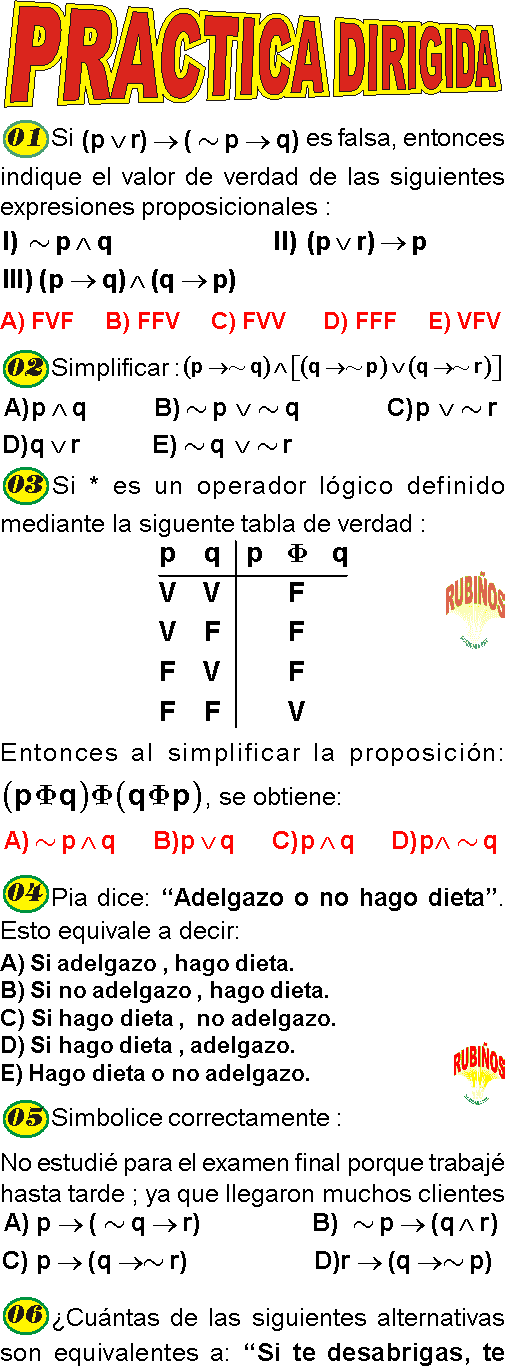
PREGUNTA 1 : 
Pia dice: ‘‘Adelgazo o no hago dieta’’. 
Esto equivale a decir: 
A) Si adelgazo , hago dieta. 
B) Si no adelgazo , hago dieta. 
C) Si hago dieta , no adelgazo. 
D) Si hago dieta , adelgazo. 
E) Hago dieta o no adelgazo. 
PREGUNTA 2 : 
La negación de la proposición Pedro no irá a ver la Copa América y no estudiará Ingeniería es 
A) Pedro no irá a ver la Copa América y estudiará Ingeniería. 
B) Pedro irá a ver la Copa América o no estudiará Ingeniería. 
C) Pedro no irá a ver la Copa América o no estudiará Ingeniería. 
D) Pedro irá a ver la Copa América o estudiará Ingeniería. 
PREGUNTA 3 : 
¿Cuántas de las siguientes alternativas son equivalentes a: 
‘‘Si te desabrigas, te resfrías’’? 
I) Si te resfrías , te desabrigaste. 
II) No te desabrigues o te resfriarás. 
III) Si no te resfrías , no te desabrigas. 
IV) No te resfrías o te desabrigas. 
A) 0 
B) 1 
C) 2 
D) 3 
E) 4 
PREGUNTA 4 : 
Enlace cada proposición compuesta con su formalización, teniendo en cuenta las siguientes proposiciones simples: 
p: las estrellas brillan 
q: la noche se ilumina 
r: la noche es agradable 
Proposiciones compuestas: 
I) Si las estrellas brillan, entonces la noche se ilumina y es agradable. 
II) Las estrellas brillan o la noche se ilumina y, por otra parte, la noche es agradable. 
III) La noche se ilumina si y sólo si las estrellas brillan y la noche es agradable. 
IV) Si no es cierto que las estrellas brillan y la noche se ilumine, entonces la no noche no es agradable.
Formalización: 
a. ( p ∨ q) ∧ r 
b. ∼( p ∧ q) → ∼ r 
c. p → (q ∧ r) 
d. q ↔ ( p ∧ r) 
Indique la secuencia correcta: 
A) IIa, IIIb, Ic, IVd 
B) Ia, IVb, IIc, IIId 
C) IIa, IVb, Ic, IIId 
D) IIIa, IVb, Ic, IId 
 PREGUNTA 5 : 
El dueño de una tienda de venta de autos desea colocar en la puerta de su establecimiento un letrero con un lema que lo identifique. Al inicio tiene como candidatos los siguientes lemas: 
I) Un buen auto no es barato. 
II) Un auto barato no es bueno. 
III) Un auto es bueno o no es barato. 
IV) Un auto no es bueno y barato a la vez. 
Su hijo , que estudia lógica , le señala que hay algunos lemas que son equivalentes ; ¿cuáles son? 
A) II y III 
B) I, II y IV 
C) I,II y III 
D) I y IV 
E) I y III 
PREGUNTA 6 : 
 Indique la secuencia correcta luego de determinar si las proposiciones son verdaderas (V) o falsas (F). 
I) ( p ∧∼ q) es lógicamente equivalente a ∼(∼ p ∨ q). 
II) (∼ p ∧ r) → q equivale lógicamente a p ∨ ∼ r ∨ q. 
III) p → q equivale a ∼p ∧ q. 
A) VVV 
B) VVF 
C) FFV 
D) FVF 
PREGUNTA 7 : 
Un anciano quiere dejar una herencia a su nieta Priscilla , pero como ésta es recién nacida , el abuelo piensa en algunas condiciones: 
I) Priscilla recibirá la herencia cuando cumpla 18 años. 
II) Si Priscilla no cumple 18 años , no recibirá la herencia. 
III) No puede ocurrir que , Priscilla cumpla 18 años y no reciba la herencia. 
Su abogado le informa que algunas de dichas condiciones son equivalentes. 
¿Cuáles son? 
A) I y II 
B) I y III 
C) II y III 
PREGUNTA 8 : 
Si las proposiciones 
a. ∼p ∨ q 
b. r → q son ambas falsas, entonces en relación con las proposiciones 
I) p es verdadera. 
II) p ∧ ∼ r es falsa. 
III) q es verdadera. 
¿cuáles son correctas? 
A) solo I 
B) solo II 
C) I y II 
D) II y III 
PREGUNTA 9 : 
Se sabe que: ‘‘El picnic del domingo no se realizará , si el tiempo no es soleado’’. 
Entonces se puede deducir válidamente que: 
A) Si se realizara el picnic , el tiempo del domingo es indudablemente soleado. 
B) Si no se realiza el picnic , el tiempo del domingo posiblemente sea nublado. 
C) Si no es un domingo soleado , el picnic no se realizará. 
D) Si es un domingo soleado , el picnic puede ser que se realice. 
E) El picnic se realizará el domingo , entonces el tiempo es soleado 
PREGUNTA 10 : 
Si la proposición ( p ∧ q) → (q → r) es falsa.
Halle el valor de verdad de las siguientes fórmulas: 
I)  ~( p ∨ r) → (p ∨ q) 
II) ( p ∨ ~ q) → (~ r ∧ q) 
III) [( p ∧ q) ∨ (q ∧ ~ r)] ↔ ( p ∨ ~ r) 
A) VVF 
B) VFV 
C) VVV 
D) VFF 
PREGUNTA 11 : 
Respecto de Si gana Perú , no voy a estudiar Indique la alternativa que se puede concluir. 
A) Si estudié , ganó Perú. 
B) Si no ganó Perú , estudié. 
C) Si no estudié , ganó Perú. 
D) Si fui a estudiar , no ganó Perú. 
E) Nunca estudio porque siempre gana Perú. 
PREGUNTA 12 : 
Los valores de verdad de las proposiciones p, q, r y s son respectivamente V, F, F y V. 
Obtenga los valores de verdad de 
I) [( p ∨ q)∨ r] ∧ s 
II) r → (s ∧ p) 
III) ( p ∨ r) → (r ∧ ~ s) 
A) VFF 
B) FVV 
C) VVV 
D) VVF 
PREGUNTA 13 : 
La siguiente expresión no es falsa . 
Si Juan no está enfermo o estudia el sábado en la noche , entonces está enfermo . 
¿Cuál de las siguientes afirmaciones es correcta? 
A) Juan estudia sábado en la mañana . 
B) Juan está enfermo . 
C) Juan no estudia el sábado . 
D) Juan va al medio . 
PREGUNTA 14 : 
Simplifique ∼(q ∨ ∼ r) → ( p ∨ ∼ p) 
A) F 
B) q 
C) p ∧ q 
D) V 
PREGUNTA 15 : 
Es falso que las clases se suspenden o la universidad cierra , si se inician las vacaciones. 
Nos han comunicado falsamente que ni las clases se suspenden ni la universidad cierra. 
Luego : 
A) Se inician las vacaciones 
B) No se inician las vacaciones 
C) Se suspenden siempre las clases 
D) Las clases no se suspenden 
E) La universidad cierra 
PREGUNTA 16 : 
Luego de elaborar la tabla de verdad de ( p ∨ ∼ q) → (∼p ∨ q), indique los valores de la matriz principal. 
A) VFVV 
B) VFVF 
C) VVVV 
D) FFVV 
PREGUNTA 17 : 
Si la proposición 
[(∼ p ∨ q) → (q ↔ r)] ∨ (q ∧ s) es falsa y p es una proposición verdadera.
Determine los valores de verdad (V) o falsedad (F) de ∼q, r y ∼s en ese orden. 
A) FFV 
B) VFV 
C) VFF 
D) FFF 
PREGUNTA 18 : 
Determine el valor de verdad (V o F) de cada una de las siguientes proposiciones y señale la alternativa que presente la secuencia correcta. 
I) Si 8 es un número par, entonces 3² es un número par. 
II) Es cierto que |√4|³=8 si y solo si 2+3= 2(3) – 1. 
III) No es cierto que los triángulos tengan cuatro vértices. 
A) VVV 
B) FVV 
C) FFF 
D) FFV 
PREGUNTA 19 : 
Se define la proposición p # q ≡ ∼p ∨ q 
Halle cuantas V y F tiene la matriz principal de ( p # ∼ q) → (∼ p # q). 
A) 2 V y 2 F 
B) 1 V y 3 F 
C) 4 V 
D) 3 V y 1 F 
PREGUNTA 20 : 
Con respecto a la proposición Si Juan es ingeniero entonces es electrónico, ¿cuáles de las proposiciones I, II y III son su equivalente? 
I) Si Juan no es electrónico entonces no es ingeniero. 
II) Juan es ingeniero y es electrónico. 
III) Juan no es ingeniero o es electrónico. 
A) solo I 
B) solo II 
C) solo III 
D) I y III 
PREGUNTA 21 : 
¿Cuáles de las siguientes proposiciones son equivalentes a ( p → q) → r? 
I) ∼[ p ∧ ∼ q ∧ ∼ r] 
II) ( p ∧ ∼ q) ∨ r 
III) (r ∨ q) ∧ (∼r ∧ q) 
A) solo I 
B) solo II 
C) solo III 
D) I y II 
PREGUNTA 22 : 
Se define p # q ≡ ∼( p → q), además la proposición 
∼{[∼p#(∼ p ↔ q)] # ( r ∨ q)} es falsa. 
Halle los valores de p, q, y r, respectivamente. 
A) VFF 
B) VFV 
C) FFF 
D) FVV 
PREGUNTA 23 : 
Si t es falsa y la proposición 
∼{(r ∨ s) → [( p ∧ ∼ s) → ( p ∧ ∼ q)]} ∨ ( t ∧ q) es verdadera.
Halle los valores de verdad de p, s, q y r. 
A) VFFV 
B) VFVV 
C) FFFF 
D) FVVF 
CLAVES – RESPUESTAS : 1)D    2)D    3)C    4)C    5)B    6)B    7)B    8)C    9)E    10)C    11)D    12)D    13)B    14)D    15)B    16)A     17)A    18)B    19)D    20)D    21)B    22)C    23)B
PROBLEMAS RESUELTOS
PREGUNTA 1 :
Una tautología es la proposición cuya negación es 
A) posible                              
B) relativamente falsa 
C) necesariamente falsa    
D) válida 
E) verdadera 
RESOLUCIÓN :
La tautología es una proposición formal necesariamente verdadera (ejemplo: ‘‘las cosas son extensas’’). Su negación será inevitablemente falsa por ser contradictoria (ejemplo: ‘‘las cosas no son extensas’’).
Expresiones que tienen la característica de ser siempre verdaderas : 
Por ejemplo : El esquema anterior es tautológico y , por tanto, su negación será necesariamente falsa : 
Rpta.: "C"
PREGUNTA 2 :
En la lógica proposicional , un ejemplo de proposición conjuntiva es: 
A) La región Chavín no limita con Loreto. 
B) El Perú , o exporta trigo o exporta arroz. 
C) El agua se congela si la temperatura está bajo cero. 
D) Si el sol brilla , el viento silba. 
E) El cielo está nublado , sin embargo hace calor. 
RESOLUCIÓN :
Una proposición conjuntiva tiene como términos de enlace ‘‘y’’, ‘‘sin embargo’’, ‘‘no obstante’’, ‘‘pero’’, etc., y une por lo menos dos proposiciones. Esto descarta a ‘‘La región Chavín no limita con Loreto’’ porque se trata de una  sola  proposición.  No  descarta ,  en  cambio , a ‘‘El cielo está nublado , sin embargo hace calor’’ , pues está compuesta por dos proposiciones y la conjunción adversativa ‘‘sin embargo’’  tiene aquí el sentido de la ‘‘y’’ lógica. ‘‘El agua se congela si la temperatura está bajo cero’’ y ‘‘Si el sol brilla , el viento silba’’ son claramente proposiciones condicionales que se estructuran con las conectivas lógicas ‘‘si ... entonces’’ .  La restante , ‘‘El Perú , o exporta trigo o exporta arroz’’, es una proposición disyuntiva fuerte. 
Rpta.: "E"
PREGUNTA 3 : 
Señale la proposición molecular. 
A) La Lógica es distinta a las Matemáticas. 
B) Deberías ser más prudente. 
C) El número 124 468 es par. 
D) Juan, María y Susy son hermanos. 
E) Si dos ángulos adyacentes forman un par lineal, entonces son suplementarios. 
RESOLUCIÓN :
Una proposición molecular es aquella que expresa más de una idea, presenta conectores o se encuentra negada. 
A continuación realizaremos un análisis de las diversas alternativas: 
A) La Lógica es distinta a las Matemáticas es una proposición atómica relacional, pues expresa solo una idea que establece una relación entre las dos ciencias. 
B) Deberías ser más prudente no es una proposición, pues es un consejo y se encuentra en función apelativa. 
C) El número 124 468 es par es una proposición simple predicativa, debido a que expresa una idea que posee un sujeto y un predicado. 
D) Juan, María y Susy son hermanos es una proposición simple relacional porque expresa una idea que establece una relación entre los tres sujetos. 
E) Si dos ángulos adyacentes forman un par lineal, entonces son suplementarios es una proposición molecular condicional, porque presenta dos ideas unidas por el conector condicional (si… entonces…). 
Rpta. : "E"
PREGUNTA 4 : 
Son afirmaciones tautológicas las siguientes: 
I) Un perro es un animal. 
II) Corrí la distancia con mis propios pies. 
III) Todo lo que está de más, se usa. 
IV) Las cosas cayeron escaleras abajo. 
V) El frío es causado por el ascenso de la temperatura. 
A) II, III, IV 
B) I, II, IV 
C) I, II, III 
D) I, II, V 
E) solo I 
RESOLUCIÓN :
Tautología es una palabra griega que significa “decir lo mismo”, es una afirmación obvia, vacía o redundante. Y por lo tanto, siempre verdadera. A continuación, analizamos los enunciados propuestos: 
I) Un perro es un animal es una tautología, pues el concepto perro está incluido dentro del concepto animal y, por lo tanto, esta expresión siempre es verdadera. 
II) Corrí la distancia con mis propios pies es una tautología, pues si alguien corre, es una verdad obvia que corre con sus pies. 
III) Todo lo que está de más, se usa esta expresión no es tautología, pues expresa una idea cuya verdad no es necesaria. 
IV) Las cosas cayeron escaleras abajo es una tautología, pues es una verdad obvia saber que las cosas caen hacia abajo. 
V) El frío es causado por el ascenso de la temperatura, es una contradicción, pues esta afirmación es siempre falsa. 
Rpta. : "B"
PREGUNTA 5: 
Simplifique 
∼ (q ∨ ∼ r) → (p ∨ ∼ p). 
A) p 
B) q 
C) p ∧ q 
D) F 
E) V 
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 6: 
Dada la siguiente proposición: 
    Si haces ejercicios, entonces mejorarás
Indique el tipo a la que pertenece. 
A) predicativas 
B) relacionales 
C) atómicas 
D) moleculares 
E) simples 
RESOLUCIÓN :
Dentro de la lógica proposicional se distingue entre proposiciones simples (atómicas) y proposiciones compuestas (moleculares); las primeras carecen de conectores o términos de enlace. 
En la proposición Si haces ejercicios, entonces mejorarás existe un conector o término de enlace (entonces); por tanto, es una proposición compuesta o molecular. 
Rpta. : "D"
PREGUNTA 7: 
Se definen las proposiciones:
p ⇓ q ≡ ∼ p ∧ q 
p ⇑ q ≡ p ∨ ∼ q 
Además, la proposición: 
∼[(q ⇓ p) → (q ⇑ r)] ≡ V 
Determine los valores de verdad de p, y r respectivamente. 
A) FFF 
B) FVV 
C) VFV 
D) VVF 
E) VVV 
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 8 : 
Si la proposición ~ q → ~ t es falsa y la proposición p↔t es verdadera, entonces el valor de verdad de las proposiciones p, q y t, en ese orden, es 
A) VFF 
B) VFV 
C) VVV 
D) FFF 
E) FVV 
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 9 : 
Sabiendo que (p ∨ q) ↔ (r ∧ s) ≡ V 
y que r y s son proposiciones con valores de verdad opuestos, ¿cuál de las siguientes proposiciones son falsas? 
a) r ∧ s 
b) p ∨ q 
c) ∼r ∨ ∼q 
A) solo a 
B) a y c 
C) solo b 
D) solo c 
E) a y b 
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 10 : 
Sabiendo que :
 (p ∧ q) ∨ (q → t) ≡ F 
¿ cuál(es) de las siguientes proposiciones son verdaderas? 
a) (∼p ∨ t) ∨ s 
b) ∼[p ∧ (∼q ∨ ∼p)] 
c) [(∼p) ∨ (q ∧ ∼t)] ↔ [(p → q) ∧ ∼(q ∧ t)] 
A) a y c 
B) todas 
C) a y b 
D) b y c 
E) solo a 
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 11: 
Simplifique la proposición siguiente: 
[(∼p ∨ q)∧(~ q ∨ r)] → (∼ r ∨ p) 
A) p 
B) q 
C) r 
D) p ∨ ∼r 
E) p ∨ q ∨ r 
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 12 : 
La proposición: “El que los nazcas hayan construido una red de canales es suficiente para distribuir el agua de los ríos y de los acueductos subterráneos. En tal sentido los canales estaban a más de diez metros de profundidad y medirán aproximadamente un metro de ancho”. 
Se formaliza: 
A) [p ← (q ∧ r)] → (s ∧ t) 
B) [p → (q ∧ r)] → (s ∧ t) 
C) [p ← (q ∨ r)] → (s ∧ t) 
D) [p → (∼ q ∧ r)] → (s ∧ t) 
E) [p →(q ∧ r)] → (s ∧ t) 
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 13 : 
En las siguientes proposiciones y luego del respectivo análisis, determinar cuáles de las siguientes proposiciones son tautologías o no. 
I) (p ∧ q) → [∼(∼p ∨ ∼q)] 
II) (p → q) ↔ [∼(p ∧ ∼q)]
III) [((p ∨ q) → ∼r) ∧ (p ∧ q)] → ∼r 
A) solo I 
B) solo I y II 
C) solo II y III 
D) I, II, III 
E) solo II 
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 14 : 
Se dan las siguientes proposiciones: 
B: Bernardo ingresó a la FIEE. 
C: Carlos ingresó a la FIEE. 
D: David ingresó a la FIEE. 
Se pide formalizar la siguiente proposición: 
“Carlos ingresó a la FIEE si es que David no lo hizo, pero si David ingresa entonces Bernardo no ingresará” 
A) (~D → C) ∨ (D → ~B) 
B) (D → ~C) ∧ (B → ~D) 
C) (C → ~D) ∨ (D → ~B) 
D) (~D → C) ∧ (D → ~B) 
E) (C → ~D) ∧ (~B → ~D) 
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 15 : 
RESOLUCIÓN :
Rpta. : "C"
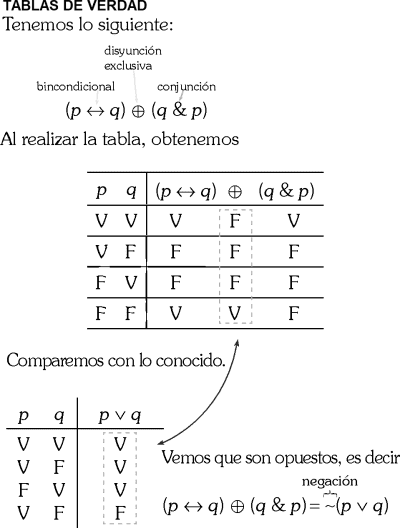
PREGUNTA 16: 
Si la proposición 
(p ∨ ∼ r) ↔ (s → w) es verdadera 
y (∼ w) → (∼ s) es falsa, 
halle el valor de verdad de las proposiciones. 
I) (p ∧ q) ∨ (r ∨ s) 
II) (s ↔ ∼ w) → (r ∧ ∼ p) 
III) [t → (w ∨ ∼ p)] ∧ ∼ (p → r) 
A) VVV 
B) VVF 
C) FFF 
D) VFF 
E) FFV 
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 17 : 
De la siguiente tabla de verdad: 
Afirmamos lo siguiente: 
1) La fórmula inferencial se encuentra ubicada en el margen superior. 
2) Presenta en el margen inferior la variable p cuatro valores de verdadero. 
3) La matriz final del esquema demuestra que es un principio lógico. 
4) La fórmula inferencial se encuentra ubicada en el cuerpo superior. 
5) La fórmula inferencial representa la regla del afirmando afirma. 
Son ciertas: 
A) 1, 2 y 3 
B) 1, 3 y 5 
C) 2, 3 y 4 
D) 2, 4 y 5 
E) 3, 4 y 5 
RESOLUCIÓN :
Rpta. : "E"
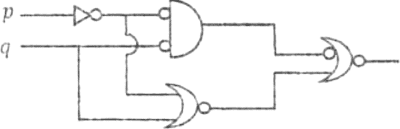
PREGUNTA 18 : 
El circuito lógico adjunto: 
Se formaliza: 
A) ∼[∼(∼ p ∧ ∼ q) ∨ ∼(∼ p ∧ q)] 
B) ∼[∼(p ∧ ∼ q) ∨ ∼(∼ p ∨ q)] 
C) ∼[∼(p ∧ ∼ q) ∨ ∼(∼ p ∧ q)] 
D) ∼[∼(∼ p ↓ q) ∨ ∼(∼ p ∨ q)] 
E) ∼[∼(∼ p ↓ ∼ q) ∨ ∼(∼ p ∨ q)] 
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 19 : 
De la expresión: 
"Casi no hay lógicos", podemos obtener equivalentemente en un universo finito: 
1) Max o Santiago son lógicos. 
2) Luis es lógico o también Gustavo es lógico. 
3) Si Jacinto no es lógico, Ervando sí lo es. 
4) Es una farsa que, ni Walter ni Carlos sean lógicos. 
5) Elvis es lógico en el caso de que Víctor no lo sea. 
SON CIERTAS: 
A) solo 1, 3 y 5 
B) solo 3, 4 y 5 
C) solo 2 y 4 
D) solo 2 y 5 
E) todas 
RESOLUCIÓN :
Rpta. : "E"
CONCEPTO 
Estudio de la aseveración a través del lenguaje. 

ENUNCIADO 
Es toda frase u oración que se utiliza en el lenguaje común, por ejemplo: 
• Lima es la capital del Perú. 
• El doble de 3 es 5. 
• ¿Qué hora es? 
• ¡Auxilio! 
• x + 2 = 7 

ENUNCIADO CERRADO O PROPOSICIÓN LÓGICA 
Es toda expresión coherente que se caracteriza por el hecho de poseer un valor de verdad o veritativo, es decir si es verdadera (V) o falsa (F) sin ambigüedad en un determinado contexto. 
Generalmente las proposiciones se denotan con letras minúsculas, como: p, q, r, s,...; por ejemplos : 
• p : Lima es la capital del Perú ( V ) 
• q : El doble de 3 es 5 ( F ) 

Los mandatos, preguntas, exclamaciones, no son proposiciones lógicas, ya que no se pueden calificar de verdaderas o falsas. 
Ejemplos: 
• ¿Qué hora es? 
• ¡Auxilio! 

ENUNCIADO ABIERTO 
Es aquel enunciado que admite la posibilidad de convertirse en una proposición lógica, cuando cada variable asume un valor determinado. 

CLASES DE PROPOSICIONES
Proposición Simple o Atómica 
Es aquella proposición que nos expresa una sola idea. 
Ejemplos : 
• p : El acero es un metal 
• q : 5² = 25 
Se llaman conectivos lógicos a las palabras que sirven para enlazar proposiciones o cambiar el valor veritativo de una proposición. 

Proposición Compuesta o Molecular 
Es aquella proposición que expresa más de una idea o la negación de una proposición. 
Ejemplos: 
• Miguel Grau fue marino y peruano. 
• La carpeta es de madera o metal 

Los valores de verdad de una o más proposiciones se pueden esquematizar por medio de una tabla de verdad como: 

PROPOSICIONES COMPUESTAS BÁSICAS 
☛ Negación (~)
☛ Conjunción
☛ Disyunción 
Inclusiva (débil) 
Exclusiva (fuerte) 
☛ Condicional 
Antecedente 
Consecuente 
☛ Bicondicional

ESQUEMAS PROPOSICIONALES 
Generalmente las proposiciones estarán formadas por varias proposiciones simples generando un esquema proposicional. 

JERARQUÍA DE LOS SIGNOS DE PUNTUACIÓN: 
TIPOS DE PROPOSICIÓN 
Tautología 
Un esquema proposicional es una tautología si al evaluar todas las posibles ordenaciones de los valores veritativos de las variables proposicionales que la componen siempre resulta verdadero. 

Contradicción 
Es una contradicción si al evaluar todas las ordenaciones de los valores veritativos de las variables proposicionales que la componen resulta falso. 

Contingencia 
Un esquema proposicional es una contingencia si su tabla de verdad contiene al menos un verdadero y al menos un falso.

EQUIVALENCIA LÓGICA 
Se llama equivalencia lógica a toda bicondicional que sea una tautología

ESQUEMAS PROPOSICIONALES LÓGICAMENTE EQUIVALENTES 
Dos esquemas proposicionales se llaman equivalentes si sus tablas de verdad son idénticas: 

LEYES DEL ÁLGEBRA PROPOSICIONAL 
☛ Idempotencia 
☛ Asociativa 
☛ Conmutativa 
☛ Distributiva 
☛ De D’Morgan 
☛ Absorción 
☛ De la condicional 

Ejercicios resueltos de examen de admisión a la Universidad