TABLAS DE VERDAD Y CONECTIVOS LÓGICOS EJERCICIOS RESUELTOS PDF
EJERCICIO 1 :
Al formalizar la proposición siguiente:
“O estás seguro y lo que dices es cierto o mientes como un bellaco”
y luego de construir su tabla de verdad. Indique el número de valores de verdad en el resultado final.
A) 6
B) 2
C) 3
D) 4
E) 5
RESOLUCIÓN :
Rpta. : "D"
EJERCICIO 2 :
Determine qué tipo de esquema molecular le corresponde a la siguiente proposición:
[(P→Q) ∧ (P→R)] → (Q→R)
A) Tautología
B) Falsedad
C) Consistencia
D) Veracidad
E) Contradicción
RESOLUCIÓN :
Los esquemas moleculares pueden clasificarse en tres: tautológicos, cuya matriz principal posee solo valores verdaderos; contradictorios, cuya matriz principal está conformada solo por valores falsos; y consistencia, formada por valores verdaderos y falsos.
La matriz principal nos da como resultado VVVVVFVV, por lo tanto al estar combinados los valores resulta ser una consistencia.
Rpta. : "C"
EJERCICIO 3 :
¿Qué alternativa es equivalente a la siguiente proposición?
(p → q) →[(p ∨ (q ∧ r)) ↔ (q ∧ (p ∨ r))]
A) p
B) p → r
C) q ↔ r
D) p ∧ ~p
E) q ∨ ~q
RESOLUCIÓN :
Rpta. : "E"
ESQUEMA MOLECULAR (Fórmula Proposicional)
Es una fórmula lógica que resulta de la combinación de variables proposicionales , constantes lógicas y signos de agrupación ; siempre y cuando sea una fórmula bien formada ( es decir que no presente ambigüedad).
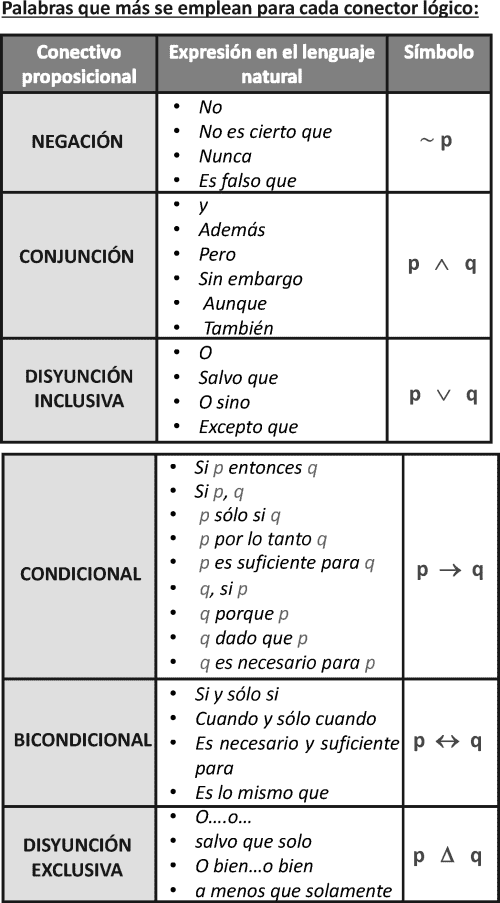
FORMALIZACION DE PROPOSICIONES
Toda proposición compuesta o todo argumento ya sea natural o científico se puede formalizar, para ello hay que distinguir las proposiciones simples que la forman y los términos de enlace que las une , a las proposiciones simples se las reemplaza con una letra que puede ser mayúscula o minúscula y al término de enlace llamado conector lógico con un símbolo convencional.
JERARQUÍA EN EL ESQUEMA MOLECULAR NEGACIÓN DE UNA PROPOSICIÓN :
Son aquellas proposiciones que hacen uso del adverbio negativo NO o sus expresiones equivalentes .
La negación consiste en cambiar el valor de verdad que tiene una proposición .
Si la proposición es «p» , su negación se denota por «p» y se lee: «no p» , «es falso que p».
En general , la negación puede reducirse a la palabra NO a la que simbolizaremos mediante
Las diferentes posibilidades las podemos esquematizar en una tabla , denominada tabla de verdad.
EJEMPLO :
Si una proposición es verdadera su negación es falsa y si una proposición es falsa su negación será verdadera.
Otras formas gramaticales equivalentes a la negación , serán : «es absurdo que» , «es inconcebible que» , «no ocurre que» , «no acaece que» , «no es el caso que» , «no es verdadero que», «no es cierto que» , «es una farsa que» , « no es el caso que», «no es imaginable que», «es inadmisible que», «es mentira que», «es falaz que»,…etc.
CONJUNTIVAS
Son aquellas proposiciones que se relacionan mediante la conjunción gramatical copulativa «y» o expresiones equivalentes. forma típica: «…y…» ejemplo :
p : Roxana comió pescado.
q : Roxana se indigestó.
La proposición quedaría: «p» y «q» :
Roxana comió pescado y se indigestó
El valor de verdad de una conjunción será dado por los valores de verdad de las proposiciones que la componen y de acuerdo a la siguiente tabla: pq es verdadera (V) únicamente cuando «p y q» son ambas verdaderas.
Otras formas gramaticales a la conjunción serán
Puesto que la conjunción gramatical de dos proposiciones cualesquiera indica la verdad simultánea de ambas , la proposición compuesta resultante es verdadera si efectivamente son verdaderas ambas ; en otros casos , la proposición resultante será falsa.
Mediante la conjunción es posible relacionar tanto proposiciones simples como compuestas , por ejemplo :
La simbolización es una representación de la «forma» o «estructura» de las frases y no una manera de «escribir la misma frase.
La lógica estudia estas formas sin tener en cuenta el contenido de información.