CIRCUITOS LÓGICOS EJERCICIOS RESUELTOS PDF
EJERCICIO 1 :
Dado el circuito lógico:
El esquema que representa es:
A) (p ∧ r) ∨ ∼ q
B) (p ∧ ∼ q) ∨ r
C) (p ∨ ∼ q) ∧ r
D) (p ∧ ∼ q) ∧ r
E) p ∨ ∼ q ∨ r
RESOLUCIÓN :
Rpta. : "C"
EJERCICIO 2 :
Sabiendo que el esquema: [(p ↔ q)→(q ∨ r)] ∨ (s → r) es falsa.
Halla el valor de verdad en:
A) VFV
B) FVV
C) FVF
D) FFV
E) VVF
RESOLUCIÓN :
Rpta. : "C"
EJERCICIO 3 :
Al reducir el circuito:
Se tiene como equivalencia:
1. –(p ← – q)
2. –(p → – q)
3. –(– p / – q)
4. –(– p ↓ – q)
5. –(p /q)
A) solo 1 y 3
B) solo 2 y 5
C) solo 4
D) 2, 4 y 5
E) 1, 3 y 4
RESOLUCIÓN :
Rpta. : "B"
EJERCICIO 4 :
Sean las proposiciones:
r =“La lógica estudia el razonamiento correcto”
s =“La lógica estudia entes científicos”
t =“La lógica estudia la verdad de la razón”
y el circuito:
Al simplificar el circuito obtenemos, equivalentemente, la proposición:
A) La lógica estudia el razonamiento correcto.
B) La lógica estudia entes científicos.
C) La lógica no estudia la verdad de hecho.
D) La lógica no estudia entes científicos.
E) No es cierto que el razonamiento lógico sea útil a la ciencia y no lo sea a la vez.
RESOLUCIÓN :
Rpta. : "A"
EJERCICIO 5 :
En el circuito:
Si cada conmutador tiene un valor de $10; el ahorro con máxima simplificación equivalente del circuito es
A) $170
B) $140
C) $160
D) $150
E) $130
RESOLUCIÓN :
Rpta. : "D"
EJERCICIO 6 :
Al reducir el siguiente circuito lógico:
RESOLUCIÓN :
Rpta. : "B"
EJERCICIO 7 :
El circuito:
Es equivalente a:
A) – p ↓ q
B) p → q
C) p /– q
D) p ← q
E) (p ∨ q) ∧ q
RESOLUCIÓN :
Formalizamos. (p ∨ – q) ∨ [ – (q ∧ – p) ∧ – q]
p ∨ – q ∨ [(– q ∨ p) ∧ – q]
p ∨ – q ∨ – q
p ∨ – q
Por lo tanto, es equivalente a p ← q
Rpta. : "D"
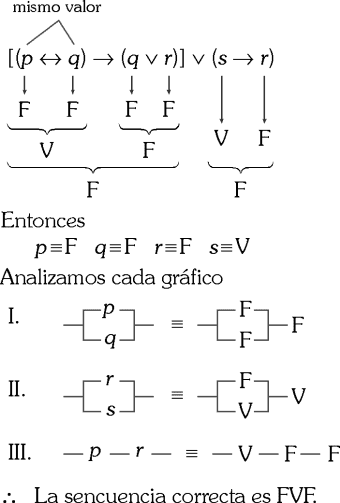
CIRCUITOS Y COMPUERTAS LÓGICAS
Son arreglos de interruptores conocidos como compuertas lógicas , donde cada compuerta lógica tiene su tabla de verdad.
El valor de verdad de una proposición puede asociarse con interruptores que controlan el paso de la corriente.
Así si una proposición es verdadera, el interruptor estará cerrado y la corriente pasará. Si la proposición es falsa el interruptor estará abierto y la corriente no pasará.
Imáginate el interruptor delante de un foco :
☛ El foco se encederá si el círculo está cerrado y pasa la corriente. (si la proposición es verdadera ).
☛ El foco no se encederá si el circuito está abierto y no pasa la corriente. (Si la proposición es falsa)
Los circuitos pueden ser :
CIRCUITOS LÓGICOS BOOLEANOS
Debido a que una proposición puede ser evaluada y resultar solo verdadera o falsa, se puede deducir alguna equivalencia con el álgebra booleana, que maneja solamente dos valores (0 y 1).
Las propiedades del cálculo proposicional son equivalentes a las del álgebra desarrollada por Boole.