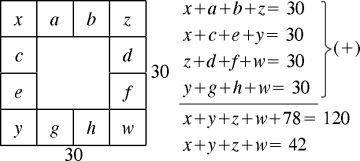RAZONAMIENTO MATEMÁTICO SAN MARCOS EXAMEN RESUELTO DE INGRESO UNIVERSIDAD

PREGUNTA 1 : 
La figura representa una estructura con forma de pirámide hexagonal hecha de hilos metálicos, Si se recorre solamente por los hilos y sin repetir ningún punto, ¿cuántas rutas distintas existen para ir desde el vértice M hasta el vértice N? 
A) 11 
B) 9 
C) 12 
D) 10 
E) 13 
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 2 : 
En una calle hay 5 casas en el orden en que muestra el gráfico, cuyos colores son azul, rojo, verde, blanco y gris. Se sabe que la casa blanca y azul tienen número impar, la casa roja tiene solo una casa al lado y esta no es de color azul, ni gris; y la casa verde no está al lado de la casa blanca. ¿De qué color es la casa que se ubica en el tercer lugar? 
A) Rojo 
B) Azul 
C) Verde 
D) Blanco 
E) Gris 
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 3 : 
Para acabar el día, hace 6 horas faltaba el triple del tiempo que faltará para acabar el día dentro de 8 horas. ¿Qué hora es? 
A) 9:00 a.m. 
B) 8:00 a.m. 
C) 10:00 a.m. 
D) 8:30 a.m. 
E) 9:30 a.m. 
RESOLUCIÓN :
2x =14 
x = 7 
∴ Hora: 24 – 15 = 9:00 a.m.
Rpta. : "A"
PREGUNTA 4 : 
Ubique los números del 1 al 12, de tal forma que la suma de los números ubicados en cada lado del cuadrado sea 30. 
Dé como respuesta el valor de x+y+z+w
A) 40 
B) 41 
C) 42 
D) 39 
E) 38 
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 5 : 
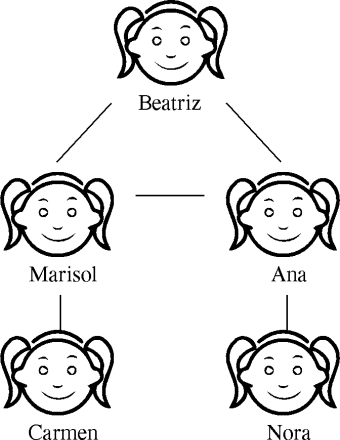
Marisol es madre de Carmen, Nora es prima de Carmen, Ana es hija de Beatriz y, a la vez, única hermana de Marisol. ¿Quién es la madre de la tía de la madre de la hija de Carmen? 
A) Ana 
B) Beatriz 
C) Marisol 
D) Carmen 
E) Nora 
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 6 : 
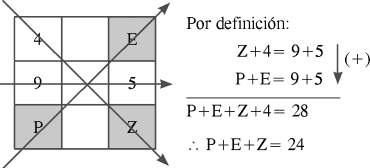
En un cuadrado mágico aditivo, la suma de los números de cada fila, columna o diagonal es siempre la misma. En el cuadrado mágico aditivo mostrado de números enteros positivos, halle el valor de P+E+Z. 
A) 35 
B) 19 
C) 28 
D) 34 
E) 24 
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 7 : 
Se tiene cuatro sólidos de mármol de forma cúbica cuyas aristas miden 5 cm. Pegándolos por una de sus caras, con estos cuatro sólidos se construye un nuevo sólido, tal como se muestra en la figura. Si en uno de los vértices del nuevo sólido se encuentra una hormiga que debe caminar a lo largo de todas las aristas de este nuevo sólido y volver al punto de partida, ¿cuál es la longitud mínima de su recorrido? 
A) 180 cm 
B) 170 cm 
C) 150 cm 
D) 140 cm 
E) 160 cm 
RESOLUCIÓN :
La figura se puede recorrer si a todos los puntos de concurrencia llegan un número par de líneas. Máximo 2 pero si inicia y termina en el mismo punto todos deben ser pares. 
Luego: 
La longitud mínima será: 
Repetición 5×5×2 + 3×5×2 + 6×5 + 4×5 + 6×5 
50 + 30 + 30 + 20 + 30 
160 cm.
Rpta. : "E"
PREGUNTA 8 : 
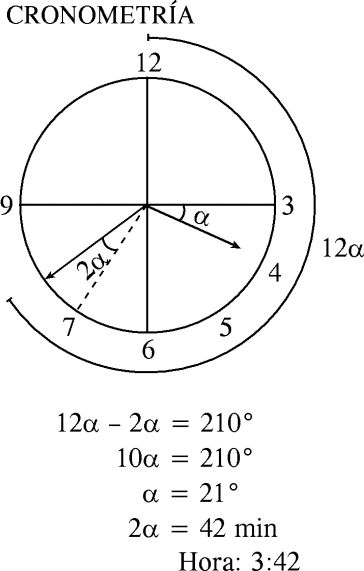
¿Qué hora indica el reloj mostrado? 
A) 3 h 42 min 
B) 3 h 44 min 
C) 3 h 43 min 
D) 3 h 41 min 
E) 3 h 36 min 
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 9 : 
En el siguiente diagrama de flujo, Anita asigna el valor 3 a N. ¿Cuál es el valor de N que se imprime al final del proceso? 
A) 10 
B) 12 
C) 18 
D) 16 
E) 14 
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 10 : 
En el plano cartesiano XY, se tiene un cuadrilátero MNPQ de vértices M(–1; 3), N(1; 5), P(3; 3) Q(0; 0). Si M’N’P’Q’ es un cuadrilátero simétrico del cuadrilátero MNPQ con respecto a la recta y=x – 1, determine la suma de las abscisas de los vértices del cuadrilátero M’N’P’Q’. 
A) 15 
B) 12 
C) – 4 
D) 13 
E) – 5 
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 11 : 
A una feria regional acudieron los ganaderos Farfán, Jáuregui, Luque y Rodríguez, procedentes de Cusco, Tacna, Puno y Arequipa, no necesariamente en ese orden, y compraron 30 ; 32 ; 45 y 50 vacunos, tampoco necesariamente en ese orden. Se debe lo siguiente. 
• Farfán procede del Cusco. 
• El que compró la mayor cantidad de vacunos proviene de Tacna. 
• La persona que viene de Puno compró la menor cantidad de vacunos. 
• Rodríguez no es el que compró la menor cantidad de vacunos en la feria.
• Jáuregui compró mayor cantidad de vacunos que Luque, pero menor cantidad que Farfán. 
Halle la suma de la cantidad de vacunos que compraron Farfán y Luque. 
A) 82 
B) 80 
C) 77 
D) 70 
E) 75
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 12 : 
El sábado 18 de noviembre de 2023, los perritos de María cumplieron 382 días de nacidos. ¿En qué día nacieron estos perritos? 
A) martes 01 de noviembre de 2022 
B) miércoles 19 de octubre de 2022 
C) martes 15 de noviembre de 2022 
D) jueves 27 de octubre de 2022 
E) martes 08 de noviembre de 2022 
RESOLUCIÓN :
De los datos, tenemos lo siguiente: (Día que nacieron) + 382 días = sábado 18 de noviembre de 2023 
En 382 días tenemos 365 días + 17 días, es decir, que nacieron hace 1 año y 17 días. 
Hace un año, desde el sábado 18 de noviembre de 2023, resultó viernes 18 de noviembre de 2022. Y de esos 17 días atrás, resultó martes 1 de noviembre de 2022. 
Rpta. : "A"
PREGUNTA 13 : 
Seis amigas, Ángela, Beatriz, Carla, Delia, Emilia y Felícita, están en una reunión. Se sabe que dos de ellas son casadas y el resto son solteras. Al preguntárseles quiénes son casadas, ellas respondieron lo siguiente: 
• Ángela: Beatriz es la casada. 
• Beatriz: Carla es la casada. 
• Carla: Emilia es la casada. 
• Delia: Yo soy soltera. 
• Emilia: Carla mintió cuando dijo que soy casada. 
• Felícita: Yo soy soltera. 
Si solamente una de las afirmaciones es verdadera, ¿quiénes son las casadas? 
A) Delia y Felícita 
B) Delia y Carla 
C) Beatriz y Felícita 
D) Emilia y Felícita 
E) Ángela y Beatriz 
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 14 : 
Con las propinas que recibió, Marita logró reunir 100 soles en monedas de 20 y 50 céntimos y monedas de 1; 2 y 5 soles. ¿Cuál es la máxima cantidad de monedas que puede tener Marita si recibió, al menos, cinco monedas de cada denominación? 
A) 294 
B) 306 
C) 298 
D) 308 
E) 296
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 15 : 
Un comerciante tiene un saco con 48 kg de arroz, una balanza de dos platillos y dos pesas, una de 3 kg y otra de 5 kg. Si un cliente le pide 11 kg de arroz y otro, 9 kg, ¿cuántas pesadas en total, como mínimo, debe realizar el comerciante para atender el pedido de ambos clientes? 
A) 2 
B) 1 
C) 3 
D) 4 
E) 5 
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 16 : 
Juan tiene seis dados convencionales e idénticos. Después de lanzar todos los dados sobre una mesa no transparente, observa que los puntos de las caras superiores de dos de ellos son cantidades impares y de los otros cuatro dados, la cantidad de puntos de sus caras superiores son pares. ¿Cuántos puntos en total, como máximo, son visibles para Juan? 
A) 112 
B) 116 
C) 120 
D) 118 
E) 96
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 17 : 
La figura representa una hoja de papel cuadriculado de la cual se desea cortar los 12 cuadrados cuyos lados miden 3 cm. ¿Cuántos cortes rectos, como mínimo, debemos realizar con una guillotina para lograr el objetivo si esta puede cortar, a lo más, tres capas de este papel? 
A) 1 
B) 4 
C) 3 
D) 5 
E) 2 
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 18 :
Sheyla, pegando 18 cubitos idénticos de madera a través de sus caras, ha construido un sólido tal como se muestra en la figura. Si el perímetro de la base inferior de dicho sólido es 30 cm, calcule el área lateral del sólido. 
A) 46 cm2
B) 50 cm2
C) 48 cm2 
D) 44 cm2 
E) 42 cm2 
RESOLUCIÓN :
Consideremos la arista de cada cubito x cm 
Perímetro de la base inferior=30x=30 
x =1cm .
·. Área de la cara lateral=30+4+4+4+4+4=50cm2
Rpta. : "B"
PREGUNTA 19 :
La figura muestra la vista horizontal, frontal y perfil derecho de un sólido de volumen máximo. Halle el número de caras que tiene dicho sólido. 
A) 12 
B) 9 
C) 11 
D) 13 
E) 10 
RESOLUCIÓN :
De las vistas anteriores, se puede deducir el siguiente gráfico en donde procedemos a contar sus caras siendo estas en total 11 caras
Rpta. : "C"
PREGUNTA 20 : 
Se tiene un recipiente lleno con 30 litros de leche y otros tres recipientes vacíos: uno de 4, otro de 6 y el tercero de 9 litros de capacidad. Ningún recipiente tiene forma regular ni marcas que permitan hacer mediciones y tampoco se permite realizar marca alguna en ellos. Utilizando solamente los recipientes, sin derramar leche, ¿cuántos trasvases se debe realizar, como mínimo, para obtener 1 litro de leche? 
A) 4 
B) 5 
C) 3 
D) 6 
E) 7 
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 21 : 
A partir del lunes 27 de marzo de 2023 a las 7:00 a. m., el reloj de Miguel se adelanta dos minutos cada hora. Determine la hora real cuando el reloj de Miguel indique las 12:50 p. m. del domingo 2 de abril de 2023. 
A) 6:00 a. m. 
B) 9:00 a. m. 
C) 7:00 a. m. 
D) 10:00 a. m. 
E) 8:00 a. m. 
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 22 : 
En un determinado instante, Luis, Manuel, Jorge y Carlos se encuentran ubicados en los vértices de un campo deportivo de forma cuadrada MNPQ. Luis está ubicado en el vértice M; Manuel, en el vértice N; Jorge en el vértice P; y Carlos en el vértice Q. Si Luis observa a Manuel en la dirección N 30º E y a Carlos en la dirección S 60º E, ¿en qué dirección observa Carlos a Manuel? 
A) N 15º O 
B) N 30º O 
C) N 20º O 
D) N 10º O 
E) N 18º O 
RESOLUCIÓN :
Por lo tanto, Carlos observa a Manuel en la dirección N 15°O.
Rpta. : "A"
PREGUNTA 23 : 
Se tiene una caja de forma de un paralelepípedo rectangular de base cuadrada cuyas dimensiones interiores son de 25cm×25cm×15cm. Se dispone de 130 barras de madera de forma de un paralelepípedo rectangular cuyas dimensiones de cada barra son 15cm×5cm×1cm. Si se coloca la máxima cantidad de estas barras dentro de la caja, ¿cuántas barras quedarán fuera? 
A) 7 
B) 6 
C) 5 
D) 3 
E) 4 
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 24 : 
Un terreno de forma rectangular, de dimensiones 56 m×72 m, es dividido completamente, de manera exacta, en parcelas cuadradas congruentes. Si, para cercar todas las parcelas por cada lado, se plantan 5 estacas igualmente separadas una de la otra (incluyendo una estaca en los vértices), ¿cuántas estacas, como mínimo, se requerirá en total? 
A) 508 
B) 486 
C) 497 
D) 506 
E) 515 
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 25 : 
En la figura, se muestran tres balanzas: las dos primeras en equilibrio y la tercera en desequilibrio; los objetos idénticos pesan igual en kilogramos enteros. ¿Cuál es el peso total de dos esferas y un cubo? 
A) 15 kg 
B) 13 kg 
C) 16 kg 
D) 12 kg 
E) 14 kg 
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 26 : 
Manuel dispone de 15 cubos idénticos, 15 cilindros idénticos y 15 esferas idénticas, algunos de los cuales lo ha colocado en la balanza 1 ; 2 y 3, como muestra la figura. Además, los objetos idénticos tienen el mismo peso. Si las balanzas 1 y 2 está en equilibrio y, en el platillo M de la balanza 3 no se debe colocar ninguna esfera, ¿con cuántos objetos, como mínimo, equilibrará Manuel las tres esferas de la balanza 3? 
A) 8 
B) 6 
C) 5 
D) 7 
E) 9 
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 27 : 
El siguiente diagrama muestra la distribución porcentual de la cantidad de los residuos domésticos generados en un distrito de Lima. Si la cantidad de residuos de papel y cartón generados es de 20 toneladas, ¿cuál o cuáles de las siguientes afirmaciones son verdaderas? 
I. La cantidad de los residuos orgánicos superan en 88 toneladas a los residuos de vidrio. 
II. La suma de las cantidades de los residuos de otros tipos y los residuos de plástico es 32 toneladas. 
III. La cantidad de residuos de plástico es 28 toneladas. 
A) II y III 
B) I y II 
C) Solo I 
D) Solo III 
E) I y III 
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 28 : 
Andrés nació el martes 12 de junio de 1975 y contrajo matrimonio el 27 de junio de 2005 en la iglesia San Pedro. ¿Qué día de la semana se casó Andrés? 
A) viernes 
B) sábado 
C) jueves 
D) domingo 
E) martes
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 29 : 
Un disco cuyo radio mide 6 cm se hace desplazar girando, sin deslizarse, desde el punto M hasta el punto T, como se representa en la figura. Si todos los obstáculos son rectángulos congruentes, cuyas dimensiones son 25cm×3cm, determine la longitud mínima que recorre el punto O, centro del disco. 
A) (2475−297√3+198𝛑)cm 
B) (2525−297√3+198𝛑)cm 
C) (2500−300√3+198𝛑)cm 
D) (2500−287√3+198𝛑)cm 
E) (2500−297√3+198𝛑)cm 
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 30 : 
Daniel y Pedro son dos amigos mitómanos que estudian en la universidad. Daniel miente los jueves, viernes y sábados, y los otros días dice la verdad. Pedro miente los domingos, lunes y martes, y los otros días dice la verdad. Un día se encuentran en la universidad y sostuvieron el siguiente diálogo: 
Daniel: "Hola ¡ayer yo mentí al decir que estudié matemática!" 
Pedro: "Hola ¡ayer yo también mentí al decir que estudié matemática!" 
¿Qué día de la semana fue el día siguiente que estudié matemática? 
A) Lunes 
B) Domingo 
C) Sábado 
D) Viernes 
E) Martes 
RESOLUCIÓN :
Rpta. : "A"
EXAMEN ANTERIOR
PREGUNTA 1 : 
Se sabe que María es madre de José y Juan es tío materno de Rosa. Si Rosa y María son hermanas de padre, respecto de José, Juan es de José. 
A) tío abuelo 
B) padre 
C) tío 
D) abuelo 
E) Hermano
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 2 : 
Un carpintero tiene un tablero rectangular de madera cuyas medidas son 120 cm de largo por 72 cm de ancho. Si de dicho tablero desea obtener piezas rectangulares de 36 cm de largo por 24 cm de ancho, y posee una sierra eléctrica suficientemente larga, ¿ cuántos cortes rectos, como mínimo, debe realizar para obtener la mayor cantidad de piezas? 
A) 6 
B) 5 
C) 3 
D) 4 
E) 1
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 3 : 
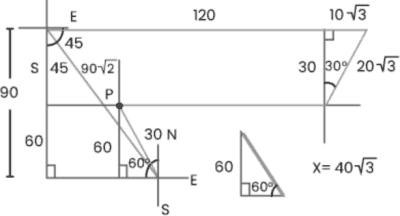
Un motociclista parte del punto P y se dirige en dirección este. Luego, recorre 20√3 km en la dirección N30ºE. Después, recorre 120 km en la dirección oeste y 90√2 km en la dirección S45ºE. Finalmente, llegó al punto P recorriendo en la dirección N30ºO. ¿Qué distancia recorrió en el último tramo? 
A) (60–√3) km 
B) 60 km 
C) 40 √3 km 
D) 30√3 km 
E) 80 km 
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 4 : 
Tres hermanas, Bertha, Lucy y Livia, tienen un total de diecisiete animales domésticos. Hay en total cinco perros y cuatro gatos, además de cierta cantidad de pericos y canarios. En la casa de Lucy, no tienen perros, pero sí un gato, dos pericos y el doble del número de canarios que tiene Livia, quien a su vez tiene un gato y un perro. En la casa de Bertha, hay dos canarios y hay por lo menos un perro, un gato y un perico. Señale la afirmación verdadera. 
I) Bertha tiene dos pericos. 
II) Lucy tiene cuatro canarios. 
III) Hay cinco canarios en total. 
A) Solo III 
B) I y II 
C) Solo II 
D) II y III 
E) Solo I 
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 5 : 
La figura adjunta muestra dos relojes. Calcule el valor de α+β. 
A) 35º 
B) 36º 
C) 38º 
D) 32º 
E) 18° 
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 6 : 
Se tienen 54 lingotes de oro de apariencia idéntica y solo uno de ellos tiene un peso menor. Con el uso de una balanza de dos platillos, ¿ cuántas pesadas como mínimo se debe realizar para identificar el lingote de menor peso? 
A) 3 
B) 4 
C) 5 
D) 2 
E) 1 
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 7 : 
Durante su entrenamiento, un boxeador da 19 golpes a una bolsa de boxeo en 8 segundos. Si el tiempo entre cada 2 golpes consecutivos es siempre el mismo y mantiene el mismo ritmo de golpe, ¿ cuántos golpes dará en 20 segundos? 
A) 46 
B) 43 
C) 45 
D) 44
E) 78  
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 8 : 
En la figura se muestran una hoja de forma rectangular cuadriculada de 12 cm de largo y 7 cm de ancho y otra hoja de forma cuadrada de 5 cm de lado. ¿Cuántas figuras congruentes con la figura (II), como máximo hay en la figura (I)? 
A) 24 
B) 32 
C) 28 
D) 21 
E) 16 
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 9 : 
La tabla adjunta muestra la cantidad de goles a favor (GF) y goles en contra (GC) de ·4 equipos de fútbol, que jugaron todos entre sí un solo partido. Si el equipo C empató todos sus partidos (el único que resultó sin goles fue el partido con D) y el equipo A ganó por un gol de diferencia al equipo D, ¿cuál fue el resultado del partido entre el equipo A y el equipo B? 
A) 2 – 0 
B) 4 – 2 
C) 3 – 1 
D) 2 – 1 
E) 1 – 0 
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 10 :  
La gráfica muestra la venta de gasolina en un grifo, durante 5 días. 
Si el precio de gasolina de 84 y 95 octanos es de S/.11 y S/.15 , respectivamente, y el día miércoles se oferta un descuento de 10% del precio de ambos tipos de gasolina, ¿cuál es la diferencia de los ingresos en la venta de los dos tipos de gasolina, durante esos 5 días? 
A) S/.164 
B) S/.276 
C) S/.254 
D) S/.264 
E) S/.194 
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 11 :
En una institución educativa se quiere construir un campo deportivo rectangular, para lo cual se diseña una maqueta, donde el largo y el ancho del rectángulo que representa el campo deportivo miden 20 cm y 10 cm respectivamente. Si la escala empleada para diseñar la maqueta es de 1:500, ¿cuál es el perímetro real del campo deportivo? 
A) 250 m 
B) 300 m 
C) 120 m 
D) 350 m
E) 260 m   
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 12 : 
En la figura, se muestra una lámina que tiene la forma de un triángulo equilátero cuyo lado mide 12 cm y MN=18 cm. Si la lámina se rota 90° sin deslizarse en sentido horario con respecto al punto N, ¿cuál es la longitud recorrida por el baricentro G del triángulo desde la posición inicial? 
A) 7√2𝛑cm 
B) 7√3𝛑cm 
C) 6√3𝛑cm
D) 2√7𝛑cm
E) 2√5𝛑cm
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 13 : 
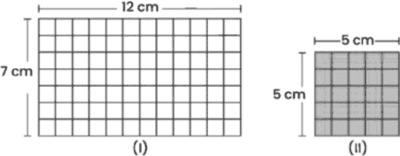
La figura, representa una malla de forma rectangular, formada por doce rectángulos congruentes cuyos lados miden a centímetros y b centímetros. Sí a<b, 3a+4b=32 y a, b son números enteros, ¿cuántos centímetros como mínimo, recorrerá la punta de un lápiz para dibujar la figura sin levantar el lápiz del papel? 
A) 158 cm 
B) 160 cm 
C) 156 cm 
D) 162 cm 
E) 172 cm 
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 14 :
Un reloj se adelanta dos minutos cada media hora. Si comienza a adelantarse a partir de las 8:30 a. m., hora exacta, y ahora marca las 11:10 a.m. del mismo día, ¿cuál es la hora correcta? 
A) 11:02 a.m. 
B) 10:56 a.m. 
C) 11:00 a.m.
D) 10:58 a.m. 
E) 10:32 a.m. 
RESOLUCIÓN :
 Rpta. : "C"
PREGUNTA 15 : 
Tres lámparas intermitentes se encienden a intervalos de 21 ; 28 y 32 segundos, respectivamente. Al inicio, todas se encienden simultáneamente. Cuando ha transcurrido una hora, ¿cuántas veces se habrán encendido simultáneamente las tres lámparas? 
A) 6 
B) 7 
C) 5 
D) 8 
E) 4
RESOLUCIÓN :
Rpta. : "A"

Ejercicios resueltos de examen de admisión a la Universidad