HABILIDAD LÓGICO MATEMÁTICA MEDICINA SAN MARCOS PRUEBA RESUELTA INGRESO UNIVERSIDAD
PREGUNTA 1 :
La empresa vitivinícola chinchana Los Catadores de Pueblo Nuevo lanza una promoción en la venta de vinos al por mayor: por la compra de cada decena de cajas de vino, al cliente se le obsequia una caja de esta bebida. Si por fiestas de fin de año, una distribuidora le compra a esta empresa 1000 cajas de vino, ¿cuál es la máxima cantidad de botellas de vino que recibió la distribuidora, si cada caja contiene una docena de botellas en este licor?
A) 14 100
B) 13 200
C) 11 000
D) 12 000
E) 13 000
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 2 :
José Luis lanza tres dados normales sobre una mesa y observa que la suma de las cifras del producto de los números que representan a la cantidad de puntos de las caras superiores de los tres dados es el menor número entero posible. Calcule la suma mínima de la cantidad de puntos que están en contacto con la mesa.
A) 9
B) 15
C) 14
D) 8
E) 7
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 3 :
Tras ser iniciada en la mañana, una reunión de negocios duró la cuarta parte del número total de horas que tiene un día. Las horas transcurridas hasta su inicio exceden en 180 minutos al tiempo que falta por transcurrir del día, desde su finalización. ¿A qué hora finalizó esta reunión?
A) 5:00 p.m.
B) 4:00 p.m.
C) 4:30 p.m.
D) 5:30 p.m.
E) 4:40 p.m.
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 4 :
Manuel tiene un balde de 12 litros de capacidad lleno de agua y dos jarras vacías, una de 9 litros y otra de 5 litros de capacidad. Ninguno de los recipientes tiene forma regular ni marcas que permitan hacer mediciones y no es posible hacerlas. Si Manuel desea obtener un litro de agua en una de las jarras sin desperdiciarla en ningún momento, ¿cuántos trasvases como mínimo debe realizar para obtener lo deseado?
A) 6
B) 4
C) 5
D) 7
E) 3
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 5 :
En el mes de diciembre de cierto año bisiesto, hubo exactamente cinco jueves, cinco viernes y cinco sábados. El Día de la Canción Criolla es una festividad peruana que se celebra el 31 de octubre de cada año. ¿Qué día de la semana del año siguiente a dicho año bisiesto se celebró el Día de la Canción Criolla?
A) Martes
B) Lunes
C) Miércoles
D) Sábado
E) viernes
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 6 :
En el siguiente arreglo rectangular, ¿de cuántas maneras diferentes se puede leer la palabra CARA, considerando la misma distancia mínima de una letra a otra en todas las lecturas?
A) 128
B) 84
C) 56
D) 112
E) 96
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 7 :
Silvia tiene varias piezas de madera, como las que se muestran en las figuras I y II. Si cada pieza está conformada por cuadraditos de 2 cm de lado, calcule el área de la región rectangular más pequeña que puede cubrir empleando ambos tipos de fichas.
A) 64 cm²
B) 80 cm²
C) 81 cm²
D) 72 cm²
E) 96 cm²
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 8 :
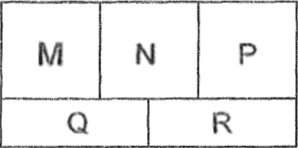
La figura representa una plancha de madera rectangular. Se dispone de una sierra que hace cortes rectos y se desea separar las partes M, N, P, Q y R. ¿Cuántos cortes rectos, como mínimo, se deberá realizar?
A) 3
B) 5
C) 2
D) 4
E) 6
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 9 :
José, que es dueño de una bodega, dispone de un saco con 50 kg de frijol canario, una balanza de dos platillos y solo dos pesas: una de 2 kg y la otra de 3 kg. Si la señora Silvia le hace un pedido de 24,5 kg de frijol, ¿cuántas pesadas como mínimo debe realizar José para cumplir con el pedido?
A) 4
B) 2
C) 3
D) 1
E) 5
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 10 :
En un tablero de ajedrez, se ubica la ficha de letra R , como se muestra en la figura. Un movimiento de la ficha de letra R consiste en avanzar 3 casillas verticalmente y 1 horizontalmente, o 3 casillas horizontalmente y 1 verticalmente. ¿Cuál es el menor número de movimientos que se debe realizar con la ficha de letra R para ir de su posición actual hasta la casilla marcada con la letra T?
A) 5
B) 4
C) 3
D) 2
E) 6
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 11 :
Cielo apila siete dados normales e idénticos sobre una superficie no transparente, como se muestra en la figura. Calcule la suma mínima de puntos visibles para Cielo.
A) 73
B) 74
C) 72
D) 75
E) 71
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 12 :
En la figura, la balanza 1 está en equilibrio. Los objetos idénticos tienen el mismo peso. Si se coloca solo objetos cuadrados, ¿cuántos deben colocarse como mínimo en la balanza 2 para que alcance el equilibrio?
A) 5
B) 1
C) 4
D) 3
E) 2
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 13 :
Se construye el triángulo ΔA’B’C’ el cual es simétrico al triángulo ΔABC usando como punto de simetría el punto que se indica en la figura. Si la hoja se utiliza como un plano coordenado y las rectas representan a los ejes coordenados, determine la suma de las abscisas de las coordenadas del nuevo triángulo ΔA’B’C’.
A) –10
B) 11
C) 12
D) –11
E) 10
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 14 :
Luz tiene tres fichas. Observa que sobre cada una de las seis caras está escrito un número entero distinto, del 2 al 7. Ella lanza sus tres fichas y en los tres lanzamientos obtiene los números que se muestran en la siguiente figura:
Calcule la suma de los números que están en las caras opuestas al 4 y al 2.
A) 10
B) 8
C) 9
D) 13
E) 11
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 15 :
Roberto hace rodar un disco, que inicialmente se encuentra en el punto Q, cuyo centro es el punto O y cuyo radio mide 2 cm, por todo el perímetro del cartón formado por una semicircunferencia, dos cuadrantes y el segmento MN, tal como se muestra en la figura. Se hace rodar el disco en sentido horario y sin deslizarse. Halle, en centímetros, la menor longitud que recorre el punto O del disco hasta el instante que el disco retorna a su posición inicial.
A) 24+14𝛑
B) 24+15𝛑
C) 24+16𝛑
D) 24+12𝛑
E) 24+11𝛑
RESOLUCIÓN :
Como el disco tiene que volver al punto inicial, es decir, rodear todo el cartón, iniciamos en el recorrido en el punto A, y delineamos el recorrido del punto O (centro del disco). En el gráfico haremos:
Rpta. : "C"