TRIGONOMETRÍA ADMISIÓN SAN MARCOS 2026 SIMULACRO RESUELTO INGRESO UNIVERSIDAD PDF
PREGUNTA 1
La figura adjunta muestra un sistema de coordenadas rectangulares, donde un móvil recorre una trayectoria rectilínea desde el punto H hacia el punto Q. Si se desplaza con velocidad constante de 50sen(–Φ) km/h desde P hasta Q, ¿en cuántos segundos recorre el segmento PQ?
A) 55
B) 40
C) 60
D) 45
E) 65
Resolución
Rpta. : "D"
PREGUNTA 2
En la figura, cotα=2, tanβ=0,6 y AB=10m.
Calcule AC.
A) 60 m
B) 48 m
C) 50 m
D) 45 m
E) 30 m
Resolución
Rpta. : "A"
PREGUNTA 3
La figura muestra un jardín limitado por el trapecio OABC. Si un jardinero desea cercar el perímetro con una malla metálica y cotq=8/15 , ¿cuántos metros de malla empleará?
A) 120 m
B) 140 m
C) 128 m
D) 132 m
E) 118 m
Resolución
Clave C
PREGUNTA 4
Las longitudes, en metros, de los lados de un terreno rectangular son 30√8sen(−α) y 60cos(–β), respectivamente. Si a y b son ángulos coterminales como se muestra en la figura y, además, cos(4𝛑+α)=2/p y cos(β+20𝛑)=p/18, ¿cuál es el área del terreno?
A) 1200 m2
B) 1600 m2
C) 1400 m2
D) 1800 m2
E) 2000 m2
Resolución
Rpta. : "B"
PREGUNTA 5
Mediante un aparato experimental se determina que la frecuencia cardiaca de una persona está dada por la expresión
pulsaciones por minuto, donde t es el tiempo en minutos después de iniciada la medición. ¿Cuántas veces la frecuencia de la persona fue de 70 pulsaciones por minuto en los 10 primeros minutos después de iniciada la medición?
A) 8
B) 5
C) 4
D) 7
E) 6
Resolución
Clave B
PREGUNTA 6
Se dispone de un papel rectangular ABCD de dimensiones 20cm y 30cm. Se hace un doblez de modo que los vertices B y D coincidan, como se muestra en la figura. Calcule el coseno del ángulo AEF.
Resolución
Rpta. : "B"
PREGUNTA 7
En la figura, se muestra un pedazo de cartulina de forma triangular, en la que se realizará un corte recto siguiendo la línea punteada. El triángulo superior obtenido será utilizado para elaborar una banderilla y el resto para otro trabajo. Si csc∝=1,25, ¿cuál es la suma de los perímetros de los dos triángulos obtenidos?
A) 48(3+√5) cm
B) 40(3+√5) cm
C) 24 (5+√5) cm
D) 48(5+√5) cm
E) 40(5+√5) cm
Resolución
Rpta. : "C"
PREGUNTA 8
La figura representa una puerta que gira, determinando en el piso la región sombreada mostrada, de área 60𝛑cm². Si la longitud del borde inferior de la puerta es 100cm, halle la medida del ángulo que giró la puerta.
A) 9𝛑/200 rad
B) 7𝛑/200 rad
C) 9𝛑/250 rad
D) 3𝛑/240 rad
E) 3𝛑/250 rad
Resolución
Rpta. : "E"
PREGUNTA 9
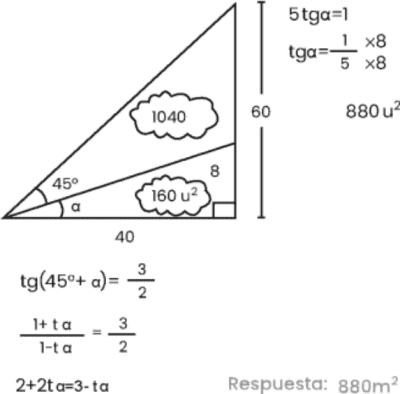
David tiene un terreno de forma triangular, como el que se muestra en la figura, y ha decidido dividir el terreno en dos regiones triangulares; ABD y ADC. Si la medida del ángulo CAD es 45°, ¿Cuál es la diferencia positiva de las áreas de estas dos regiones triangulares?
A) 820 m2
B) 760 m2
C) 800 m2
D) 840 m2
E) 880 m2
Resolución
Rpta. : "E"
PREGUNTA 10
A partir del PBI anual de un país, a un economista le interesa estimar su inflación anual g(x). Para ello emplea la siguiente fórmula empírica:
Donde x es el PBI expresado en miles de millones de dólares. Si el PBI que se estima para el año 2023 está entre 3,14 y 4,71 (miles de millones de dólares), indique el intervalo de la inflación anual aproximada esperada (considerar 𝛑≈3,14).
A) 〈1/10;1/2〉
B) 〈–1/10;1/2〉
C) 〈–1/2;1/4〉
D) 〈–1/10;1/5〉
E) 〈1/5;1/2〉
Resolución
Rpta. : "E"
PREGUNTA 11
Para tomar el jugo que está en el interior de una caja que tiene forma de un prisma rectangular recto se coloca uña cañita, como se representa en la figura. Halle la longitud de la cañita.
Resolución
Rpta. : "C"
PREGUNTA 12
La Sra. Lourdes tiene un pequeño jardín rectangular en el patio de su casa, cuyos lados miden 2|4sen5°cos5°cos70°–cos10°|m y 4(4cos5°cos55°–2cos50°)m. Si para sembrar rosas y begonias coloca una cerca en la diagonal de su jardín, halle la longitud de la cerca.
A) √13 m
B) 3 m
C) √19 m
D) 6 m
E) 7 m
Resolución
Rpta. : "C"
PREGUNTA 13
La función fα: ℝ+→ℝ , definida por fα(x)=tanαx, donde α es un parámetro entero positivo, representa el cambio de temperatura de un cuerpo. Se requiere saber la suma de los valores de x sobre el intervalo ]𝛑/4;4𝛑/3[ donde no es posible definir la siguiente expresión:
f1(x) + f2(x) + f3(x)
A) 9𝛑/2
B) 11𝛑/2
C) 11𝛑/6
D) 14𝛑/3
E) 9𝛑/3
Resolución
Rpta. : "A"