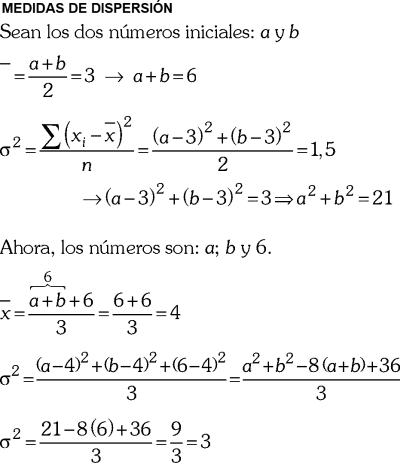MATEMÁTICA UNSA PRUEBA RESUELTA SAN AGUSTIN INGRESO UNIVERSIDAD

PREGUNTA 1 :

Teresa invita a sus amigas al cine. Si dispone de S/32, le faltaría dinero para comprar entradas de S/5; pero si adquiere entradas de S/4, le sobraría dinero. El número de amigas que invitó Teresa es:

A) 3

B) 4

C) 5

D) 6

E) 7

RESOLUCIÓN :

Sea x: el número de entradas que compra (Teresa y sus amigas)

Dinero que dispone =S/32

Si compra entradas de S/5, le falta dinero

5x>32

⇒ x> 6,4

Si compra entradas de S/4, le sobra dinero

4x<32

⇒ x<8

El valor que satisface ambas ecuaciones es x=7

Por lo tanto, el número de amigas que Teresa invita es 6

Rpta. : "D"

PREGUNTA 2 :

Sabiendo que la razón geométrica de dos números cuya diferencia de cuadrados es 180, se invierte al sumar 6 al menor y restar 6 al mayor. Calcule su producto.

A) 180

B) 216

C) 270

D) 396

E) Hay dos respuestas.

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 3 :

En un examen para el ingreso a la universidad, el 60% de mujeres y el 70% de hombres aprobaron el examen. Si el total de mujeres es el 80% del total de personas, entonces el porcentaje del total de personas que no aprobaron el examen es:

A) 35%

B) 30%

C) 38%

D) 40%

E) 42%

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 4 :

A los términos de una proporción geométrica le sumamos una misma cantidad y se obtiene los números 27; 11; 54 y 20 respectivamente. Calcule la suma de los términos de dicha proporción.

A) 119

B) 100

C) 99

D) 204

E) 129

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 5 :

Haydee, Karla, Janina y Anita van a una pensión y al salir de compras dejan encargada a la dueña que les deje una porción de uvas. Llega primero Haydee y extrae la cuarta parte. Después llega Karla y saca una cuarta parte de lo que queda. Posteriormente llega Janina y come una cuarta parte de lo que hay en la canasta. Por fin llega Anita y saca una cuarta parte del resto y se retiran a dormir. Si quedaron 81 uvas, entonces la cantidad de uvas que hubo al principio fue:

A) 160

B) 185

C) 220

D) 240

E) 256

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 6 :

Pedro tiene 600 soles y desea comprar un reloj que vale 180 soles sólo con los intereses generados por dicho capital. En una financiera que oferta una tasa de interés del 5% semestral, el número de años en que podrá comprar el reloj es:

A) 1

B) 2

C) 3

D) 4

E) 5

RESOLUCIÓN :

REGLA DE INTERÉS

Se tiene los datos:

C=S/600

I =S/180

r%=5% semestral<>10% anual

T=??

Se sabe que

I=C×r%×T

Reemplazando:

180=600×10%T

∴ T=3 (años)

Rpta. : "C"

PREGUNTA 7 :

En el siguiente cuadro se observa la cantidad de alumnos matriculados en los talleres de un centro educativo:

Si cada alumno solo puede matricularse a un taller, ¿cuál es la cantidad de alumnos matriculados en los tres talleres?

A) 21

B) 27

C) 32

D) 34

E) 37

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 8 :

Un padre de familia repartió una cantidad de dinero entre sus tres hijos de 10 ; 12 y 14 años de edad. Si el reparto fue inversamente proporcional a las edades, recibiendo el mayor 420 soles, ¿cuál es la cantidad repartida?

A) S/1686

B) S/1224

C) S/5880

D) S/1498

E) S/1500

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 9 :

Los padres de Leonard y Leonety poseen una tienda de golosinas. Un lunes Leonard come 6 caramelos y Leonety 7 galletas; el martes Leonard come 13 caramelos y Leonety 11 galletas; el miércoles Leonard come 20 caramelos y Leonety 15 galletas y así sucesivamente. El último día Leonard come 83 caramelos y Leonety 51 galletas, día en que se terminaron los caramelos y galletas. ¿En cuántos días se terminaron los caramelos y galletas?

A) 8

B) 13

C) 15

D) 10

E) 12

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 10 :

A) 42°

B) 21°

C) 63°

D) 32°

E) 48°

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 11 :

El cuadrado de la edad de Roberto, menos 3 es mayor que 165. En cambio, el doble de su edad, más 3 es un número menor que 30.

¿Qué edad tiene Roberto?

A) 13 años

B) 15 años

C) 18 años

D) 20 años

E) 10 años

RESOLUCIÓN :

Sea la edad de Roberto =x (x es entero positivo).

De acuerdo con los datos:

• El cuadrado de la edad de Roberto menos 3 es mayor que 165.

x² – 3 > 165

⇒ x² > 162

⇒ x >12,7…

• El doble de su edad, más 3 es un número menor que 30.

2x+3 < 30

⇒ 2x < 27

⇒ x < 13,5

Luego se tiene 12,7… < x < 13,5

⇒ x=13

Por lo tanto, la edad de Roberto es 13 años.

Rpta. : "A"

PREGUNTA 12 :

La siguiente figura (histograma) representa los puntajes obtenidos por 500 postulantes a la Escuela de Administración. Determine la media aritmética de los puntajes obtenidos.

A) 53

B) 52

C) 54

D) 50

E) 51

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 13 :

En una reunión de 30 profesionales entre médicos y odontólogos: 22 son hombres, 14 son odontólogos y 2 son médicos y mujeres. Para cierta tarea se eligen al azar y, a la vez, a 5 profesionales. Si las personas elegidas resultan ser mujeres, halle la probabilidad de que sean odontólogas.

A) 5/16

B) 7/32

C) 3/28

D) 3/36

E) 6/14

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 14 :

Si Fabián depositó los 4/5 de su capital a una tasa del 2% mensual durante dos meses y el resto a una tasa del 4% trimestral, durante seis meses. Calcule el capital de Fabián si en total recibió S/104 864, sabiendo que se aplica un interés compuesto.

A) S/120 000

B) S/200 000

C) S/90 000

D) S/180 000

E) S/100 000

RESOLUCIÓN :