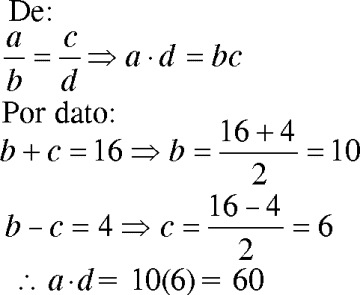ARITMÉTICA UNSA PRUEBA RESUELTA SAN AGUSTIN INGRESO UNIVERSIDAD
PREGUNTA 1 :
Sean a y b números naturales en:
Entonces, la suma de todos los valores posibles de b es:
A) 15
B) 16
C) 21
D) 25
E) 27
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 2 :
¿Cuántos rectángulos diferentes existen de lados enteros y de área igual a 36u2?
A) 3
B) 4
C) 5
D) 6
E) 7
RESOLUCIÓN :
b×h=36
1×36
2×18
3×12
4×9
∴ Existen 4 rectángulos.
Rpta. : "B"
PREGUNTA 3 :
Halle la fracción equivalente a 5/11 , talque la diferencia de sus términos sea 120. Elija como respuesta el denominador.
A) 100
B) 200
C) 220
D) 400
E) 50
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 4 :
En una proporción geométrica, la suma de los términos medios es 16 y la razón aritmética de los mismos es 4. Calcule el producto de los extremos.
A) 60
B) 64
C) 48
D) 72
E) 80
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 5 :
En un barco había 180 personas, ocurre un naufragio y de los sobrevivientes, 2/5 fuman, 3/7 son casados y los 2/3 son ingenieros. El número de personas que murieron en dicho accidente es:
A) 60
B) 65
C) 70
D) 75
E) 80
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 6 :
La diferencia entre el mayor y el menor término de una proporción geométrica continua es 25. Si el otro término es 30; calcule la suma de los términos diferentes si dicho términos son enteros positivos.
A) 95
B) 105
C) 115
D) 425
E) 135
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 7 :
El producto de dos números es 181 272. Si al multiplicador se le resta 27 unidades, resulta como producto 161 616. Hallar la suma de las cifras del mayor número.
A) 13
B) 15
C) 17
D) 19
E) 21
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 8 :
Dada la siguiente relación
a+b+c+d=35
hallar el valor de:
M=d–c+b–a
A) 4/7
B) 7/2
C) 7
D) 14
E) 21/2
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 9 :
En una caja hay 200 caramelos de dos sabores, limón y naranja , los cuales están en una relación de 3 a 1. ¿Cuál es la diferencia del número de caramelos que hay en la caja?
A) 50
B) 100
C) 150
D) 170
E) 180
RESOLUCIÓN :
# de caramelos de Limón : 3k
# de caramelos de Naranja : k
Según enunciado : 3k + k = 200
⇒ 4k = 200 ⇒ k = 50
Piden : 2k = 100
Rpta. : "B"
PREGUNTA 10:
Una obra debe terminarse en 30 días empleando 20 obreros, trabajando 8 horas diarias. Después de 12 días de trabajo, se pidió que la obra se terminara 6 días antes del plazo establecido y así se hizo. El número de obreros que se aumentaron, teniendo presente que se aumentó también en dos horas el trabajo diario, es:
A) 4
B) 24
C) 14
D) 18
E) 9
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 11 :
En la bodega Los Pioneros, se mezclan dos clases de café en razón de 5 a 3 y se vende ganando el 15%. Después se hace otra mezcla en razón de 3 a 5 y se vende ganando el 20%, resultando ambos precios de venta iguales. Halle la razón de sus precios unitarios.
A) 51/43
B)25/31
C) 43/77
D) 77/21
E) 50/44
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 12 :
¿En qué sistema de numeración n se cumple que la suma de todos los números de dos cifras, tal que la primera cifra sea la mitad de la segunda, es 132 en base n?
A) binario
B) quinario
C) senario
D) octal
E) nonario
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 13 :
Julián deposita S/1000 hoy, después de 2 meses hará otro depósito de S/500. Determine el monto que retirará dentro de 6 meses, si la entidad bancaria le paga 1,5 % de interés simple mensual.
A) S/1620
B) S/1590
C) S/135
D) S/120
E) S/1635
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 14 :
Calcula el MCD de dos números sabiendo que el producto es 4 860 y el MCM es 270.
A) 9
B) 16
C) 15
D) 12
E) 18
RESOLUCIÓN :
Sean A y B los números.
Por propiedad, se cumple que: A×B=MCD(A;B)×MCM(A;B)
Entonces: 4860=MCD(A; B) ×270
⇒ MCD(A; B) =18
Rpta. : "E"
PREGUNTA 15 :
Luis desea obtener en 5 años S/50 000. Si la institución financiera le paga una tasa del 12% simple anual, ¿cuánto debe depositar hoy para recibir ese monto en los 5 años?
A) S/25 000
B) S/31 250
C) S/33 150
D) S/28 250
E) S/31 250
RESOLUCIÓN :
Capital: N
Tasa: 12% anual
Tiempo: 5 años
Sabemos que M=C+ I M=C+C× r%×T
Reemplazando los datos, obtenemos
50 000=N+N×12%5
50 000=160%N
∴ 31 250=N
Rpta. : "B"
PREGUNTA 16 :
Se invierte un capital de S/30 000 en un proyecto que paga el 5% anual, ¿cuál es el interés simple generado si el proyecto tuvo una vida útil de 2 años y medio?
A) 4000
B) 4500
C) 3750
D) 3500
E) 3720
RESOLUCIÓN :
C=S/30 000
r%=5% anual
T= 2,5 años
Piden el interés simple generado.
Sabemos que I=C×r%×T
Reemplazamos los datos.
I = 30000 × 5% × 2,5
I =300×12,5
∴ I =3750
Rpta. : "C"
PREGUNTA 17 :
Calcule el área (en metros) de un triángulo, cuya base mide 0,4 dam y su altura mide 600 cm. Seleccione la mejor respuesta.
A) 10 m2
B) 8 m2
C) 11 m2
D) 12 m2
E) 20 m2
RESOLUCIÓN :
Rpta. : "D"
