NÚMEROS PRIMOS EJERCICIOS RESUELTOS PDF
El estudio de los números primos fue abordado por matemáticas desde hace mucho tiempo. Fue el matemático griego EUCLIDES el primero en descubrir que los números primos constituyen una serie infinita (Aprox. 350 a.c.)
- CLIC AQUÍ Ver CRIBA DE ERASTÓSTENES
- Ver REGLA PARA SABER SIN UN NÚMERO ES PRIMO
- Ver DESCOMPOSICIÓN CANÓNICA
- Ver CANTIDAD DE DIVISORES
- Ver SUMA DE DIVISORES
- Ver PRODUCTO DE DIVISORES
- Ver SUMA DE INVERSAS DE DIVISORES
- Ver INDICADOR DE UN NÚMERO
- Ver NÚMEROS PERFECTOS AMIGOS SATURADOS
APRENDIZAJES ESPERADOS
☛ Reconocer los números simples, primos y compuestos.
☛ Reconocer los números PESI y sus propiedades.
☛ Descomponer canónicamente un número entero positivo.
☛ Calcular la cantidad y suma de divisores de un número entero positivo.
CLASIFICACIÓN DE LOS NÚMEROS ENTEROS POSITIVOS
Según su cantidad de divisores ℤ+; la clasificación será:
NÚMEROS SIMPLES
Son aquellos que poseen a lo más dos divisores.
A su vez:
LA UNIDAD
Es el único número entero positivo que posee un solo divisor (él mismo).
LOS NÚMEROS PRIMOS
Llamados también primos absolutos , son aquellos que poseen exactamente dos divisores (la unidad y el mismo número); estos son:
2 ; 3 ; 5 ; 7 ; 11 ; 13 ; 17 ; 19 ; 23 ; …
NÚMEROS COMPUESTOS
Son aquellos que poseen más de dos divisores; estos son:
4 ; 6 ; 8 ; 9 ; 10 ; 12 ; 14 ; 15 ; 16 ; …
Todo número compuesto posee por lo menos un divisor primo.
PROPIEDADES DE LOS NÚMEROS PRIMOS
☛ El conjunto de los números primos absolutos es infinito.
{2; 3; 5; 7; 11; 13; 17; 19; …}
☛ El único número primo par es el 2, los demás son impares.
☛ Los únicos números que son consecutivos y primos a la vez son el 2 y el 3.
☛ Los tres únicos números impares consecutivos y primos a la vez son el 3; 5 y 7.
NÚMEROS PRIMOS ENTRE SÍ (PESI)
Llamados también números “primos relativos” o “coprimos”, son aquellos que poseen un solo divisor común: La unidad.
PROPIEDADES DE LOS NÚMEROS PESI
☛ Dos números enteros positivos y consecutivos siempre son PESI.
☛ Dos números impares positivos y consecutivos siempre son PESI.
☛ Si en un conjunto de más de dos números enteros positivos al menos dos de ellos son números PESI, entonces todo el conjunto de números son PESI.
TEOREMA FUNDAMENTAL DE LA ARITMÉTICA
Todo número entero positivo mayor que la unidad se puede expresar como el producto de sus divisores primos diferentes, elevados cada uno de ellos a exponentes enteros positivos, dicha representación es única a excepción del orden de sus factores y se le denomina “Descomposición Canónica”(D.C).
INDICADOR DE UN NÚMERO O FUNCIÓN DE EULER
Es la cantidad de números enteros positivos menores que un número dado y primos con él.
PRIMERA PRACTICA
EJERCICIO 1 :
¿Cuál es el primer número primo de tres dígitos?
A) 105
B) 103
C) 101
D) 102
E) 107
EJERCICIO 2 :
¿Cuál es el tercer número primo de dos dígitos?
A) 23
B) 15
C) 17
D) 19
E) 13
EJERCICIO 3 :
¿Cuál es el menor número primo de dos dígitos?
A) 10
B) 11
C) 12
D) 13
E) 14
EJERCICIO 4 :
¿Cuál es el mayor número primo de dos dígitos?
A) 99
B) 89
C) 97
D) 96
E) 91
EJERCICIO 5 :
¿Cuántos números primos hay entre 8 y 20?
A) 4
B) 5
C) 6
D) 7
E) 8
EJERCICIO 6 :
¿Cuántos números primos hay entre 4 y 18?
A) 5
B) 6
C) 7
D) 8
E) 9
EJERCICIO 7 :
De los siguiente números: 29 ; 37; 28; 51; 65; 53; 71
Indicar cuántos son compuestos
A) 1
B) 2
C) 0
D) 3
E) 4
EJERCICIO 8 :
Indicar qué grupo de números son PESI.
I)18 ; 20 ; 15
II) 24 ; 25 ; 26
III)15 ; 17 ; 23
IV) 19 ; 21 ; 23
A) I y II
B) I, II y IV
C) I, III, IV
D) II, III y IV
E) II y IV
EJERCICIO 9 :
De los siguientes números , indica cuántos son primos.
59; 19; 27; 31; 47; 33; 91; 92
A) 3
B) 4
C) 2
D) 5
E) 6
EJERCICIO 10 :
Descomponer 120 como producto de factores primos.
A) 2×3³×5
B) 2×3×5²
C) 2²×3³×5
D) 2³×3²×5
E) 2³×3×5
EJERCICIO 11 :
Descomponer canónicamente el número 540.
A) 2×3³×5²
B) 2×3×5²
C) 2²×3³×5
D) 2³×3²×5
E) 2²×3²
EJERCICIO 12 :
Descomponer 240 en sus factores primos.
A) 3²×5
B) 2²×3²×5
C) 2⁴×3×5
D) 2³×3×5²
E) 2³×3×5
EJERCICIO 13 :
Descomponer canónicamente el número 3600.
A) 2³×3²×5
B) 2⁴×3²×5²
C) 2⁴×3²×5²
D) 2³×3×5²
E) 2²×3³×5
EJERCICIO 14 :
¿Cuál de las alternativas es un número primo?
A) 123
B) 117
C) 75
D) 97
E) 84
EJERCICIO 15 :
Hallar la suma de los números primos comprendidos entre 36 y 62.
a) 18
B) 29
C) 31
D) 33
E) 35
EJERCICIO 16 :
Marcar la alternativa que tenga un grupo de números PESI.
A) 24; 55; 36
B) 15; 25; 75
C) 64; 16; 24
D) 14; 35; 21
E) 17; 31; 47
EJERCICIO 17 :
Hallar la descomposición canónica (D.C.) de 378000
A) 2⁴×3²×5³×7
B) 2⁵×3³×5³×7
C) 2⁴×3³×5²×7²
D) 2³×3⁴×5²×7
E) 2⁴×3³×5³×7
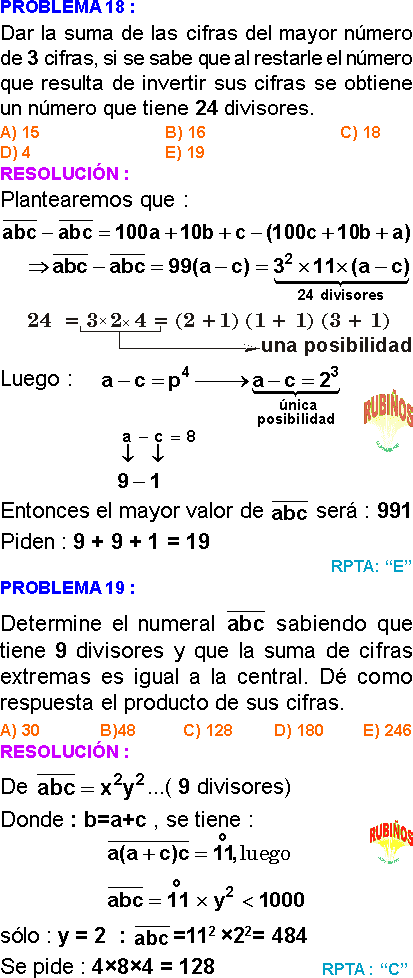
EJERCICIO 18 :
Hallar la descomposición canónica de 155232
A) 25×3³×7²×11
B) 2⁴×3²×7²×11
C) 2⁶×3²×7²×11
D) 2⁵×3²×7³×11
E) 2⁵×3²×7²×11
EJERCICIO 19 :
Si: 5600 =2x×5y×7z, calcular : x + y +z
A) 5
B) 7
C) 8
D) 6
E) 9
EJERCICIO 20 :
Si: 160083 =3a×7b×11c, calcular a+b×c
A) 10
B) 6
C) 7
D) 8
E) 9
EJERCICIO 21 :
Indicar verdadero (V) o falso (F), según corresponda y dar como respuesta, ¿cuántas son verdaderas?
☛ El mayor número primo de 2 cifras es 97 ( )
☛ Si un número no es compuesto entonces es primo ( )
☛ Si la suma de dos números primos resulta impar entonces uno de ellos necesariamente es ( )
☛ Los únicos números primos que se diferencian en 1, son el 2 y el 3 ( )
☛ Todos los números pares son compuestos ( )
☛ Dos números compuestos no pueden ser primos entre sí ( )
☛ El 1 no es primo ( )
A) 6
B) 5
C) 4
D) 3
E) 2
EJERCICIO 22 :
La edad de Claudia es la suma de los 5 primeros números primos, menos 8. ¿Cuál es la edad de Claudia?
A) 20
B) 28
C) 21
D) 22
E) 19
EJERCICIO 23 :
Hallar la descomposición canónica de 3600
A) 2³×3²×5²
B) 2²×3²×5²
C) 2⁴×3³×5²
D) 2×3³×5²
E) 2⁴×3²×5²
EJERCICIO 24 :
¿Cuántos divisores compuestos tiene el número 24?
A) 2
B) 5
C) 9
D) 6
E) 10
EJERCICIO 25 :
Indicar que grupo de números son PESI:
I) 18 ; 28 ; 35
II) 20 ; 22 ; 36
III) 29 ; 30 ; 38
IV) 18 ; 51 ; 66
A) I y II
B) II y IV
C) II y III
D) I, II y III
E) I y III
SEGUNDA PRACTICA
PREGUNTA 1 :
¿Cuánto suman los divisores pares de 30?
A) 22
B) 15
C) 16
D) 20
E) 18
PREGUNTA 2 :
¿Cuántos divisores tiene el 400?
A) 18
B) 12
C) 15
D) 16
E) 10
PREGUNTA 3 :
La suma de divisores de 50 es:
A) 95
B) 92
C) 93
D) 102
E) 103
PREGUNTA 4 :
De los divisores de 40, ¿cuántos son impares?
A) 1
B) 2
C) 3
D) 4
E) 5
PREGUNTA 5 :
¿Cuántos divisores primos tiene el 300?
A) 2
B) 3
C) 4
D) 5
E) 1
PREGUNTA 6 :
¿Cuántos divisores simples tiene el 180?
A) 2
B) 3
C) 4
D) 5
E) 1
PREGUNTA 7 :
De los divisores del 60, ¿cuántos son pares?
A) 5
B) 4
C) 3
D) 2
E) 6
PREGUNTA 8 :
Dado el número : M=2⁵×3²×7³
Calcular su cantidad de divisores
A) 30
B) 45
C) 72
D) 54
E) 60
PREGUNTA 9 :
Cuántos divisores tiene : N=3⁴×7²×11⁵
A) 81
B) 90
C) 40
D) 54
E) 64
PREGUNTA 10 :
Sea:
a = cantidad de divisores de 60
b = cantidad de divisores de 100
Calcular: "a + b"
A) 21
B) 20
C) 19
D) 18
E) 17
PREGUNTA 11 :
Sea:
a = cantidad de divisores de 120.
b = cantidad de divisores de 180.
Calcular: b – a
A) 4
B) 5
C)1
D) 2
E) 3
PREGUNTA 12 :
Si : N=2⁴×5³×7×112n tiene 280 divisores.
Calcular "n"
A) 1
B) 2
C) 4
D) 6
E) 3
PREGUNTA 13 :
Hallar el valor de "n" para que el número N=12×9n tenga 42 divisores.
A) 5
B) 4
C) 6
D) 7
E) 3
PREGUNTA 14 :
Hallar el valor de "n" para que el número M=25n×15 tenga 24 divisores.
A) 1
B) 5
C) 4
D) 2
E) 3
PREGUNTA 15 :
Si número B =22n×3²×7⁵ tiene 122 divisores compuestos. Calcular "n"
A) 2
B) 3
C) 4
D) 5
E) 6
PREGUNTA 16 :
Hallar el valor de "n" para que el número A=2³×3×5n×7⁴ tenga 75 divisores compuestos.
A) 2
B) 1
C) 3
D) 4
E) 5
PREGUNTA 17 :
Si número M = 2⁵×33n×5²×13² tiene 539 divisores propios.
A) 1
B) 2
C) 4
D) 3
E) 5
PREGUNTA 18 :
Hallar n para que el número N=2³×3n×52×7n tenga 187 divisores compuestos.
A) 1
B) 3
C) 5
D) 7
E) 9
PREGUNTA 19 :
Dado el número: B = 2⁵×3⁴×7³
Calcular el número de divisores compuestos.
A) 120
B) 121
C) 116
D) 119
E) 115
PREGUNTA 20 :
Si el número M = 32n×52n×7⁴ tiene 124 divisores propios. Calcular «n»
A) 2
B) 1
C) 4
D) 3
E) 5
PREGUNTA 21 :
¿Cuántos divisores más tiene el 240 que el 350?
A) 12
B) 8
C) 16
D) 10
E) 6
PREGUNTA 22 :
Dado el número M=2⁶×5³×7⁴. Calcular el número de divisores compuestos y divisores propios.
A) 136 y 139
B) 137 y 139
C) 137 y 140
D) 135 y 138
E) 136 y 140
PREGUNTA 23 :
Si: A = 2⁴×3²×5n×11² tiene 315 divisores. Calcular «n»
A) 4
B) 2
C) 3
D) 6
E) 5
PREGUNTA 24 :
Si: B = 2⁴×3n×5⁶×7² tiene 630 divisores. Calcular n
A) 6
B) 4
C) 3
D) 5
E) 2
PREGUNTA 25 :
Calcular «a» para que el número A=2a×3a×5a×7² posee 76 divisores compuestos.
A) 1
B) 2
C) 3
D) 4
E) 5
TERCERA PRACTICA
PROBLEMA 1 :
¿Cuántos divisores primos tiene 130130?
A) 3
B) 4
C) 5
D) 6
E) 7
Rpta. : "C"
PROBLEMA 2 :
Calcular la suma de los divisores positivos de 48.
A) 126
B) 143
C) 124
D) 77
E) 98
Rpta. : "C"
PROBLEMA 3 :
¿Cuántos divisores positivos comunes tienen los números 3780; 5940 y 1080?
A) 36
B) 16
C) 12
D) 24
E) 4
Rpta. : "D"
PROBLEMA 4 :
El cociente del primer número primo mayor que 505 entre el primo anterior, con tres decimales de aproximación es:
A) 1,031
B) 1,001
C) 1,011
D) 1,021
E) 1,041
Rpta. : "C"
PROBLEMA 5 :
¿ Cuántos de los siguientes números son primos absolutos en base 7 ?
13(7) ; 31(7) ; 61(7) ; 25(7)
A) 0
B) 1
C) 2
D) 3
E) 4
Rpta. : "C"
PROBLEMA 6 :
Determine el valor de ‘‘n’’ sabiendo que el mínimo común múltiplo de
A=180ⁿ×27 y B=40ⁿ×60 tiene 5400 divisores.
A) 6
B) 7
C) 8
D) 9
E) 10
Rpta. : "C"
PROBLEMA 7 :
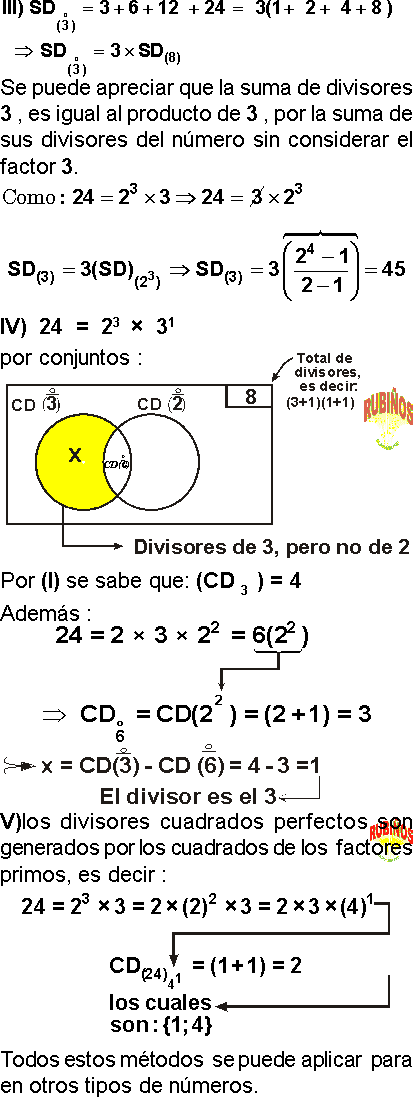
De los divisores de 24, averiguar :
I) ¿Cuántos son múltiplos de 3?
II) ¿Cuántos no son múltiplos de 3?
III) La suma de divisores múltiplos de 3
IV) ¿Cuántos son múltiplos de 3 , pero no de 2?
V) ¿Cuántos son cuadrados perfectos ?
PROBLEMA 8 :
¿Cuántos números primos hay entre 10 y 500 que al restarle 2 resulta potencia de 3?
A) 5
B) 2
C) 4
D) 3
E) 6
Rpta. : "D"
PROBLEMA 9 :
Sea N =3y×5z. Al dividir N entre 3 se suprimen 6 divisores y al dividir N entre 5 se suprimen 4 divisores. Hallar y+z.
A) 10
B) 5
C) 8
D) 7
E) 6
Rpta. : "C"
PROBLEMA 10 :
Si N² tiene 63 divisores y N³ tiene 130 divisores ¿cuántos divisores tiene N⁴? Calcule la suma de las cifras de esta cantidad.
A) 4
B) 5
C) 6
D)7
E)8
Rpta. : "B"
PROBLEMA 11 :
Si la suma de la cantidad de divisores de 8ⁿ y 10ⁿ es 86. ¿Cuántos divisores cuadrados perfectos tiene 12ⁿ?
A) 28
B) 30
C) 32
D) 34
E) 36
Rpta. : "C"
PROBLEMA 12 :
Si el número 2457 ×11b×aa tiene 27 divisores primos con 3549 , entonces a + b es :
A) 8
B) 15
C) 9
D) 12
E) 10
Rpta. : "E"
PROBLEMA 13 :
Hallar la cantidad de divisores de N⁴.
Dato I : la cantidad de divisores de N² es 35
Dato II: La cantidad de divisores de N³ es 70
Dato III: La cantidad de divisores de N⁵ es 121
el problema se resuelve con :
A) I
B) II
C) I y II
D) III
Rpta. : "C"
PROBLEMA 14 :
Dos números descompuestos en su forma canónica, se expresan como:
A= a2m(a + 2)3nb⁹ ; B = a2m+1(a + 2)n11³
Si A y B tienen 54 divisores comunes , siendo A el menor posible. ¿Cuántos divisores impares tiene A?
A) 9
B) 16
C) 24
D) 144
E) 131
Rpta. : "D"
PREGUNTA 1 :
María le pregunté a Jorge por la fecha de su cumpleaños; él responde el n de noviembre. Si P=25×36ⁿ tiene 243 divisores, ¿qué fecha cumple años Jorge?
A) 4 de noviembre
B) 6 de noviembre
C) 8 de noviembre
D) 7 de noviembre
E) 5 de noviembre
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 2 :
Se tiene dos valores enteros positivos A, B tales que el valor de
M=(A² – 4B²) es primo positivo.
Si M toma el valor mínimo, calcule A+B.
A) 6
B) 9
C) 13
D) 15
E) 4
RESOLUCIÓN :
Rpta. : "E"
LA CRIBA DE ERATÓSTENES
Eratóstenes (276 a.C – 194 a.C) fue un científico y filósofo de la Antigua Grecia que realizó trabajos en astronomía, geografía, matemáticas y también en poesía e historia.
La criba de Eratóstenes es un algoritmo que permite hallar todos los números primos menores que un número natural dado. Se forma una tabla con todos los números naturales comprendidos entre 2 y n; y se van tachando los números que no son primos de la siguiente manera: Comenzando por el 2, se tachan todos sus múltiplos; comenzando de nuevo, cuando se encuentra un número entero que no ha sido tachado, ese número es declarado primo, y se procede a tachar todos sus múltiplos, así sucesivamente.
El proceso termina cuando el cuadrado del siguiente número confirmado como primo es mayor que ”n”.