ÁNGULO TRIGONOMÉTRICO Y SISTEMAS DE MEDIDAS ANGULARES CONVERSIÓN SEXAGESIMAL CENTESIMAL Y RADIAL EJERCICIOS RESUELTOS DE TRIGONOMETRÍA PREUNIVERSITARIA PDF
El estudio de las matemáticas y la necesidad de cuantificar ha requerido, desde la Antigüedad, apoyarnos en sistemas de referencia.
Por ejemplo, cuando se quería medir una distancia, se utilizaban diversos sistemas de referencia como el pie, la cuarta, la yarda, entre otros.
El problema con este tipo de unidades es que no se eliminaba la ambigüedad, es decir, se fomentaba el uso de diferentes medidas en los diversos pueblos, lo que dificultaba las diversas actividades como el comercio, donde tenían que ponerse de acuerdo sobre las cantidades con las que se estaban negociando.
A finales del siglo XVIII , en Francia se adopta el llamado sistema métrico.
La ventaja de este sistema es doble (por una parte proporciona una única unidad para cada magnitud física), además, no es necesario el uso de factores de conversión puesto que todos los múltiplos y submúltiplos de la unidad son potencias de diez.
En el caso de los ángulos, la necesidad de darle unidades de medición no ha sido la excepción.
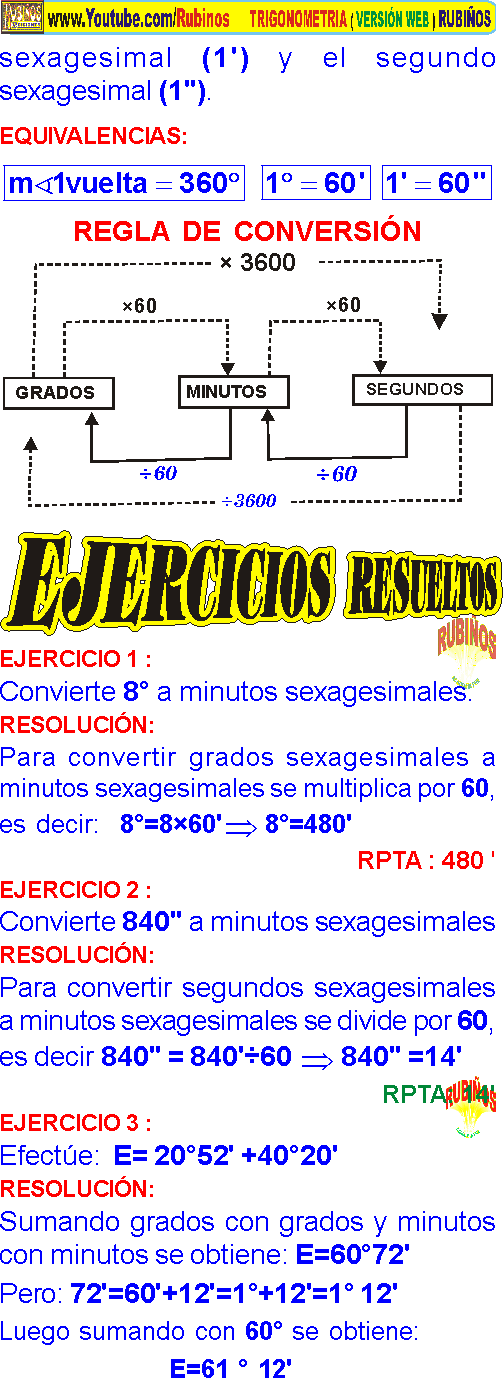
Por ejemplo, en las culturas antiguas, los babilonios adoptaron la unidad sexagesimal, que se mantiene hasta la actualidad por su practicidad.
Asimismo se han ido creando instrumentos para medirlos tales como el sextante, el goniómetro, el compás, entre otros, los cuales buscarán siempre una mayor precisión.
ANGULO TRIGONOMÉTRICO
Es aquel que se genera por la rotación de un rayo alrededor de un punto fijo (O) llamado vértice desde una posición inicial (lado inicial) hasta una posición final (lado final).
ÁNGULO DE UNA VUELTA
Se genera por la rotación completa de un rayo; es decir, su lado final coincide con su lado inicial por primera vez.
Cuando a un ángulo trigonométrico se le invierte su sentido, su valor cambia de signo.
Para sumar dos o más ángulos trigonométricos, gráficamente es necesario que estén en un mismo sentido.
- CLIC AQUÍ Ver ÁNGULO TRIGONOMÉTRICO EJERCICIOS RESUELTOS
- Ver SISTEMAS DE MEDIDAS ANGULARES
- Ver FÓRMULAS DE CONVERSIÓN
- Ver LONGITUD DE ARCO
- Ver SECTOR CIRCULAR
- Ver RUEDAS VUELTAS APLICACIONES DE LA LONGITUD DE ARCO
CREADORES DE LA TRIGONOMETRÍA
Generalmente se considera como creador de la Trigonometría al griego Hiparco de Nicea (150 a.C.), quien recopiló en unalista la posición de 1 000 estrellas fijas y confeccionó una tabla de funciones trigonométricas con ayuda de la cual halló la distancia de la Tierra a la Luna.
Fue Claudio Ptolomeo quien sistematizó la Trigonometría de entonces, enriqueciéndola con nuevas fórmulas y procedimientos. Publicó su inmortal obra Al Magisti o Almagesto cuyos métodos eran tan correctos que aún siglos más tarde se enseñaban en distintas universidades llegando a constituir la base de las tablas astronómicas que facilitaron los descubrimientos de Enrique el Navegante y Cristóbal Colón. Fue autor de la teoría geocéntrica del sistema solar así como de importantes obras que por muchos siglos fueron la única fuente de consulta, hasta la aparición de Copérnico, Galileo y Kepler.
Modernamente, descuellan en el perfeccionamiento de la Trigonometría Francisco Viete, Leonardo Euler y John Kepler.
















































.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)

