LONGITUD DE ARCO EJERCICIOS RESUELTOS PDF – TRIGONOMETRÍA
CÁLCULO DE LA LONGITUD DE UN ARCO
APRENDIZAJES ESPERADOS
• Reconocer que los arcos tienen dos tipos de medición: angular y lineal.
• Dibujar correctamente un sector circular y reconocer sus elementos.
• Calcular correctamente la longitud de un arco y aplicar la fórmula de manera eficiente a la resolución de ejercicios de interpretación y aquellos que contienen gráficos.
En el estudio de la matemática , se denomina arco a cualquier curva continua que une dos puntos.
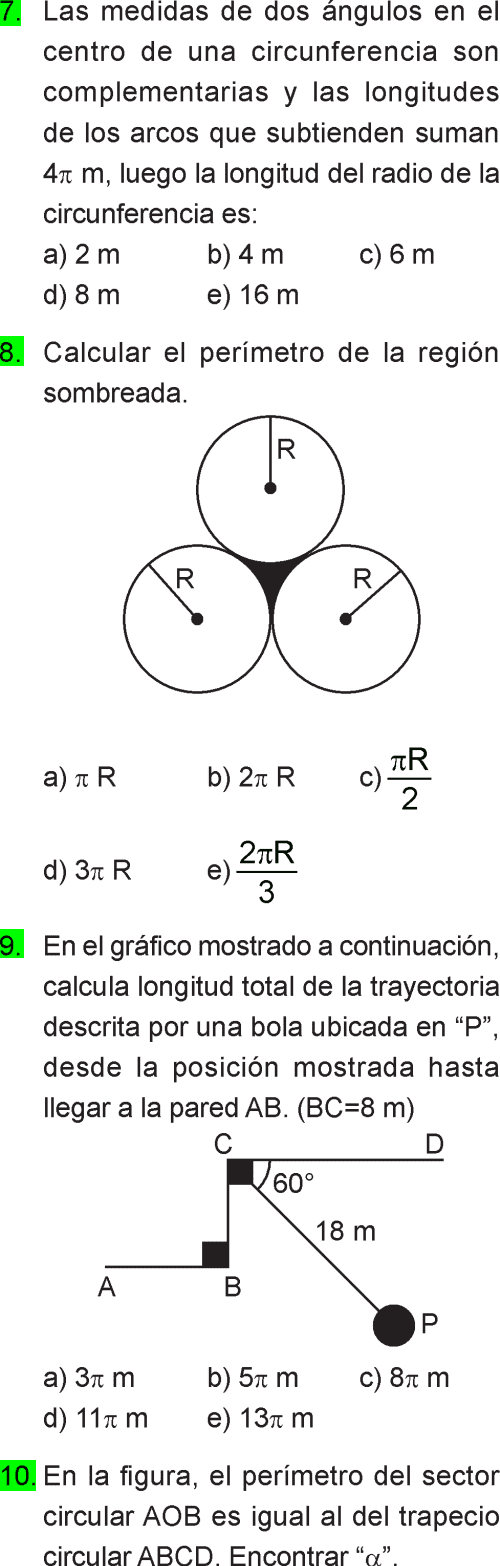
En la actualidad es una herramienta importante para la ingeniería, arquitectura, mecánica, astronomía, entre otros.
Un arco en particular es cuando esta curva corresponde a una circunferencia y, a partir de ello, se puede estudiar el comportamiento de un punto que se desplaza por el arco de una circunferencia y el número de vueltas que pueda desarrollar.
De esta manera se puede entender el principio que sigue el movimiento de las ruedas, poleas y engranajes cuando estas desarrollan una cantidad determinada de vueltas.
En el caso de un arco irregular, muchos grandes pensadores consideraron imposible calcular su longitud.
Las primeras mediciones se hicieron a través de métodos de aproximación: trazaron polígonos dentro de la curva, calcularon la longitud de cada uno de sus lados para luego sumarlos y así obtener una aproximación a la longitud de la misma.
Mientras más segmentos usaban, disminuía la longitud de cada uno, con lo cual lograban aproximarse cada vez más a la longitud de dicha curva.
Más adelante, en el siglo XVII, se lograron desarrollar otros métodos que permitieron determinar soluciones más precisas para obtener las longitudes de los arcos de diversas curvas.
CIRCUNFERENCIA
Conjunto de puntos del plano que equidistan de un punto fijo llamado centro.
A la distancia común del centro a los puntos del plano que verifican lo anterior se le denomina radio de la circunferencia.
A la porción de circunferencia limitada por dos puntos de ella se le denomina arco
LONGITUD DE ARCO :
Se denomina arco a una porción cualquiera de una curva
GUIA DE CLASE
PREGUNTA 1 :
Calcular la longitud de arco que corresponde a un ángulo central de 50° en una circunferencia de diámetro 36m.
A) 25𝛑m
B) 5𝛑m
C) 10𝛑m
D) 20𝛑m
E) 15𝛑m
Rpta. : "B"
PREGUNTA 2 :
En un sector circular, se cumple que el arco mide 2𝛑 y el radio mide 6. ¿Cuál es la medida sexagesimal del ángulo central?.
A) 10°
B) 20°
C) 60°
D) 40°
E) 90°
Rpta. : "C"
PREGUNTA 3 :
En un sector circular, el ángulo central mide 36° y el arco correspondiente mide 6𝛑cm. ¿Cuál es la longitud del radio de dicho sector?.
A) 10m
B) 20m
C) 30m
D) 15m
E) 5m
Rpta. : "C"
PREGUNTA 4 :
En un sector circular, el ángulo central mide 72° y el radio 20 cm. ¿Cuánto mide el arco?.
A) 𝛑m
B) 2𝛑
C) 3𝛑
D) 4𝛑
E) 8𝛑
PREGUNTA 5 :
En un sector circular la longitud del arco es 6𝛑cm, y el ángulo central mide 30g. ¿Cuánto mide su diámetro?
A) 60cm
B) 80cm
C) 100cm
D) 120cm
E) 70cm
PREGUNTA 6 :
Calcular la longitud de un arco, correspondiente a un ángulo central de 60º en una circunferencia de 24m de radio.
A) 6𝛑m
B) 7𝛑m
C) 8𝛑m
D) 5𝛑m
E) 10𝛑m
PREGUNTA 7 :
Calcular la longitud de un arco correspondiente a un ángulo inscrito de 15º en una circunferencia de 24dm de radio.
A) 4𝛑dm
B) 5𝛑dm
C) 6𝛑dm
D) 3𝛑dm
E) 8𝛑dm
PREGUNTA 8 :
En un sector circular, la longitud del arco es 4𝛑cm y el ángulo central mide 50g. ¿Cuánto mide su diámetro?
a) 28cm
b) 30
c) 32
d) 24
e) 16
PREGUNTA 9 :
Calcular la longitud de un arco, correspondiente a un ángulo central de 72º en una circunferencia de 25m de radio.
A) 10𝛑m
B) 11𝛑
C) 12𝛑
D) 13𝛑
E) 16𝛑
PREGUNTA 10 :
Calcular la longitud de un arco correspondiente a un ángulo inscrito de 24º en una circunferencia de 36dm de radio.
A) 8,6𝛑dm
B) 9,6𝛑
C) 10,6𝛑
D) 4,8𝛑
E) 8,8𝛑
PREGUNTA 11 :
En un sector circular la medida del radio y el arco están representados por dos números enteros consecutivos. Si el perímetro del sector es 17cm. ¿Cuál es la medida del radio?
a) 3cm
b) 4
c) 5
d) 6
e) 8
PREGUNTA 12 :
En un sector circular la medida del arco y el radio están representados por dos números enteros consecutivos. Si el perímetro del sector es 20cm. ¿Cuál es la medida del ángulo central?
a) 4/3 rad
b) 3/4
c) 2/3
d) 3/2
e) 1/2
PREGUNTA 13 :
Un tramo de una carretera está formada por dos arcos de circunferencia, el primero tiene un radio de 18km y un ángulo central de 40º, el segundo tiene un radio de 36km y un ángulo central de 50º.
Hallar la longitud total de este tramo. (𝛑=22/7)
a) 35km
b) 42
c) 56
d) 40
e) 50
PREGUNTA 14 :
Un tramo de una carretera está formada por dos arcos de circunferencia, el primero tiene un radio de 9km y un ángulo de 20º, el segundo tiene un radio de 72km y un ángulo central de 60º. Hallar la longitud total de este tramo.
A) 24𝛑km
B) 25𝛑
C) 26𝛑
D) 30𝛑
E) 20𝛑
PREGUNTA 15 :
A un alumno se le pide calcular la longitud de un arco correspondiente a un ángulo central de 30º; pero el inscribe 30g obteniendo un arco de longitud 9𝛑/2 cm. Halle la verdadera longitud del arco.
A) 𝛑cm
B) 3𝛑
C) 4𝛑
D) 2𝛑
E) 5𝛑
PREGUNTA 16 :
En un sector circular, se cumple que el arco mide 6𝛑 y el radio mide 6. ¿Cuál es la medida sexagesimal del ángulo central?.
A) 10°
B) 20°
C) 90°
D) 40°
E) 60°
PREGUNTA 17 :
En un sector circular, el ángulo central mide 36° y el arco correspondiente mide 6𝛑m. ¿Cuál es la longitud del radio de dicho sector?.
A) 10m
B) 20m
C) 30m
D) 15m
E) 5m
PREGUNTA 18 :
Calcular la longitud de arco que corresponde a un ángulo central de 50° en una circunferencia de diámetro 36m.
A) 25𝛑m
B) 5𝛑
C) 10𝛑
D) 20𝛑
E) 15𝛑
PREGUNTA 19 :
Calcular la longitud de un arco cuyo ángulo central correspondiente mide 10ᵍ y el radio del sector mide 10m.
A) 𝛑m
B) 2𝛑
C) 𝛑/2
D) 4𝛑
E) 5𝛑
PREGUNTA 20 :
Calcule la longitud del radio de una circunferencia en la que un ángulo central , que comprende un arco que mide 61(𝛑/50)m , tiene una medida en grados centesimales representada por un número entero y en grados sexagesimales representaba en la forma x°x’.
A) 3m
B) 4m
C) 2m
D) 2,5m
E) 3,5m
Rpta. : "C"
PROBLEMAS PROPUESTOS
PREGUNTA 1 :
Se tiene un sector circular de 6 cm de radio y 12 cm de longitud de arco. Si el radio aumenta en 2 cm sin que el ángulo central varíe. ¿Cuál será la nueva longitud de arco?
a) 8 cm
b) 10 cm
c) 12 cm
d) 14 cm
e) 16 cm
Rpta. : "E"
PREGUNTA 2 :
Un péndulo oscila describiendo un ángulo cuya medida es 28° y un arco de longitud 66 cm. Encontrar la longitud del péndulo, en m. (Considerar: 𝛑 = 22 7 )
a) 0,135
b) 1,35
c) 13,5
d) 135
e) 1350
Rpta. : "B"
PREGUNTA 3 :
En un sector circular la longitud de su arco es 1 m. Si su ángulo central se aumenta en 10% y su radio se disminuye en 10%, se determina un nuevo sector circular cuya longitud del arco, en cm , es:
a) 0,99
b) 1
c) 10
d) 99
e) 100
Rpta. : "D"
PREGUNTA 4 :
Se tiene un sector circular de 6cm de radio y 12cm de longitud de arco. Si el radio aumenta 2cm sin que el ángulo varíe, ¿ Cuál será la nueva longitud de arco ?
a) 12 cm
b) 14 cm
c) 16 cm
d) 18 cm
e) 20 cm
Rpta. : "D"
PREGUNTA 5 :
En un sector circular, el quíntuplo de la longitud de su radio es igual al cuádruplo de su longitud del arco respectiva; luego la medida de su ángulo central es:
a) 1 rad
b) 0,40𝛑 rad
c) 1,25𝛑 rad
d) 0,40 rad
e) 1,25 rad
Rpta. : "E"
PREGUNTA 6 :
Sí a un sector circular le duplicamos el ángulo central y a su radio le aumentamos 3m, se obtendrá un nuevo sector cuya longitud de arco es el quíntuple de la longitud del arco inicial. Determine el radio del sector inicial.
a) 1m
b) 2m
c) 3m
d) 4m
e) 5m
Rpta. : "B"
PREGUNTA 7 :
Dos ángulos en el centro de una circunferencia son complementarios y las longitudes de los arcos que subtienden suman 4𝛑 m. Calcular la longitud del radio de la circunferencia.
a) 2m
b) 4m
c) 6m
d) 8m
e) 10m
Rpta. : "D"
PREGUNTA 8 :
Determinar la longitud de una circunferencia, sabiendo que en ella un ángulo central que mide 20g determina una longitud de arco igual a 𝛑 u.
a) 100𝛑 u
b) 100 u
c) 10𝛑 u
d) 20 u
e) 20𝛑 u
Rpta. : "E"
PREGUNTA 9 :
Si a un sector circular le triplicamos su radio y a su ángulo central le añadimos 60°, se obtendrá un nuevo sector de longitud de arco igual al quíntuple de la longitud del arco inicial. Calcule el ángulo central del nuevo sector.
a) 2𝛑/3 rad
b) 3π/4 rad
c) 4𝛑/3 rad
d) 3𝛑/7 rad
e) 5𝛑/6 rad
Rpta. : "E"
PREGUNTA 10 :
Hallar el diámetro de la circunferencia en la cual un ángulo inscrito de 30° subtiende un arco con 11 m de longitud. (Usar 𝛑 = 22/7 )
a) 11 m
b) 21 m
c) 22 m
d) 42 m
e) 44 m
Rpta. : "B"
PREGUNTA 11 :
El ángulo central que subtiende un arco de radio 36 mide C rad, si se disminuye dicho ángulo hasta que mida S rad. ¿Cuánto debe aumentar el radio para que la longitud de dicho arco no varié? (S y C son lo convencional)
a) 2
b) 4
c) 6
d) 8
e) 10
Rpta. : "B"
PREGUNTA 12 :
Las medidas de dos ángulos en el centro de una circunferencia son complementarias y las longitudes de los arcos que subtienden suman 4𝛑 m, luego la longitud del radio de la circunferencia es:
a) 2 m
b) 4 m
c) 6 m
d) 8 m
e) 16 m
Rpta. : "D"
PREGUNTA 13 :
En un sector circular se conoce que su radio mide (x+1)cm, su longitud de arco 9(x–1)cm, y la medida de su ángulo central correspondiente (x²–1) rad. Hallar el valor de "x".
a) 9
b) 4
c) 3
d) 2
e) 1
Rpta. : "D"
PREGUNTA 14 :
Una plantilla circular de cartulina, de 30 cm de radio se divide en 3 regiones equivalentes que tienen forma de sector circular. Con cada sector circular se construye la superficie lateral de un cono. Si se sabe que para construir la base del cono que tiene forma circular se necesita de su radio, calcule la longitud del radio de la base del cono resultante.
A) 25 cm
B) 15 cm
C) 10 cm
D) 30 cm
E) 20 cm
Rpta. : "C"
PREGUNTA 15 :
Lucerito está muy ansiosa esperando en la casa de su abuelito a su amiguita Fabiana para poder ir al cine. Por tal motivo, está continuamente mirando la hora y mientras tanto, se percata que el péndulo del reloj que tiene 84 cm de longitud se balancea y se desplaza 15° a cada lado respecto a la vertical. Con la información dada, determine la longitud de arco que describe.
A) 7𝛑 cm
B) 12𝛑 cm
C) 14𝛑 cm
D) 8𝛑 cm
E) 10𝛑 cm
Rpta. : "C"
PREGUNTA 16 :
Si el péndulo de un reloj de pared mide 4 cm y su punta recorre un arco de 5°37'30'' por segundo, ¿cuántos metros recorre en un minuto el arco que describe la punta del péndulo?
A) 𝛑/40 m
B) 𝛑/20 m
C) 3𝛑/8 m
D) 7𝛑/40 m
E) 3𝛑/40 m
Rpta. : "E"
PREGUNTA 17 :
La puerta de la biblioteca Amauta es de tipo vaivén. En base a ello, calcule la longitud de la trayectoria descrita por el extremo del borde inferior de la puerta al girar un ángulo de 135°, si dicho borde mide 112 cm.
A) 81𝛑 cm
B) 80𝛑 cm
C) 82𝛑 cm
D) 84𝛑 cm
Rpta. : "D"
PREGUNTA 18 :
Un vehículo viaja a la velocidad de 60 km/h en una pista circular de radio 20 m, recorriendo parte de ella en un tiempo de 𝛑 seg. ¿Cuánto mide en radianes el ángulo generado en ese tiempo?
A) 𝛑/6
B) 2𝛑/3
C) 5𝛑/6
D) 𝛑/3
Rpta. : "C"
PREGUNTA 19 :
Calcule la longitud del recorrido que realiza el minutero desde las 3: 00 pm., hasta las 3:20 p.m. Considere que la longitud del minutero es de 12 cm.
A) 3𝛑 cm
B) 8𝛑 cm
C) 5𝛑 cm
D) 9𝛑 cm
Rpta. : "B"
PREGUNTA 20 :
El minutero de un reloj mide 15 cm, calcule la distancia que recorre su extremo al cabo de 18 minutos.
A) 3𝛑 cm
B) 2𝛑 cm
C) 5𝛑 cm
D) 9𝛑 cm
Rpta. : "D"
PREGUNTA 21 :
Se tiene una lámina de cobre en forma de un sector circular cuyo ángulo central (200/3)g . Si se desea cubrir el arco con una cinta de 6𝛑/7 cm, este no queda cubierto totalmente, pero si es cubierto con un cinta cuya longitud es de 10𝛑/7 cm, sobra una longitud dos veces más de la que faltaba anteriormente. Calcule el radio de la lámina.
A) 1 cm
B) 2 cm
C) 4 cm
D) 3cm
Rpta. : "D"
PREGUNTA 22 :
Los brazos de un columpio miden 1,8 m de largo y pueden describir como máximo un ángulo de 150°. Calcule el espacio recorrido por el asiento del columpio cuando el ángulo descrito en su balanceo es el máximo.
A) 3,5𝛑 mm
B) 1,5𝛑 m
C) 𝛑 m
D) 2,5 𝛑 m
Rpta. : "B"