SISTEMAS ANGULARES EJERCICIOS RESUELTOS PDF TRIGONOMETRÍA

SISTEMA SEXAGESIMAL CENTESIMAL RADIAL DE MEDICIÓN ANGULAR Y SUS CONVERSIONES

APRENDIZAJES ESPERADOS 

• Reconocer un ángulo trigonométrico. 

• Reconocer el sistema sexagesimal. 

• Realizar conversiones entre grados, minutos y segundos sexagesimales. 

• Reconocer el sistema radial. 

• Aprender a convertir la medida de un ángulo de un sistema a otro.

PRACTICA

PREGUNTA 1 : 

Calcula el equivalente de 20^g. 

a) 10° 

b) 9° 

c) 𝛑/4 rad 

d) 𝛑/10 rad 

e) 𝛑/18 rad 

Rpta. : "D"

PREGUNTA 2 : 

Calcula el equivalente de 𝛑/48 rad. 

a) 2°15’ 

b) 3°15’ 

c) 2°45’ 

d) 3°45’ 

e) 5°15’ 

Rpta. : "D"

PREGUNTA 3 : 

Calcula el equivalente de 𝛑/12 rad. 

a) 10° 

b) 10^g

c) 15° 

d) 15^g

e) 24° 

Rpta. : "C"

PREGUNTA 4 : 

Convierte a centesimal : 81’’ 

a) 50^s 

b) 150^s 

c) 250^s  

d) 200^s  

e) 125^s 

Rpta. : "C"

PREGUNTA 5 : 

Convierte a centesimal : 27´ 

a) 5^m

b) 50^m

c) 25^m

d) 30^m 

e) 45^m

Rpta. : "B"

PREGUNTA 6 : 

Se tienen dos ángulos suplementarios, tales que el doble del menor es igual al mayor disminuido en 30°. Halla el mayor en radianes. 

a) 13𝛑/7 rad 

b) 13𝛑/20rad 

c) 13𝛑/18rad 

d) 5𝛑/18rad 

e) 𝛑/18rad 

Rpta. : "C"

PREGUNTA 7 : 

La suma de dos ángulos es 80g y su diferencia es 18°. Encuentra uno de los ángulos en sexagesimales. 

a) 40° 

b) 45° 

c) 82° 

d) 13°

e) 15° 

Rpta. : "B"

PREGUNTA 8 : 

Si se cumple que: 2°62’ 63” = a°a’a” 

Halla “a” . 

a) 1 

b) 2 

c) 3 

d) 4 

e) 5 

Rpta. : "C"

PREGUNTA 9 : 

Calcula un ángulo en radianes, si cinco veces la medida en centesimales menos cuatro veces la medida en sexagesimales, todo multiplicado por la medida en radianes es igual a 2,8𝛑. 

a) 𝛑/5 rad 

b) 𝛑/4 rad 

c) 𝛑/10 rad 

d) 𝛑/6 rad 

e) 𝛑/100 rad 

Rpta. : "C"

PREGUNTA 10 : 

Si el doble del número que expresa el complemento de un ángulo en sexagesimal es igual al número que expresa su suplemento en centesimales. Halla la medida internacional de dicho ángulo. 

a) Absurdo 

b) 𝛑/8 rad 

c) 𝛑/16 rad 

d) – 𝛑/16 rad 

e) – 𝛑/8 rad 

Rpta. : "E"

Los instrumentos de medición que fue creando el científico para ayudarse en la investigación permitieron recoger los datos sobre los que se basarían los posteriores cálculos que procesarían la información tomada de los hechos . 

Expresar la medida de los ángulos en términos del ángulo de una vuelta no es muy común y poco práctico , para ello utilizamos los sistemas de medidas angulares. 

Los sistemas de medición angular fueron inventados con la finalidad de medir con exactitud y precisión al ángulo , siendo tres los sistemas más conocidos , los cuales son : sexagesimal , centesimal y radial, siendo el primero muy utilizado en aplicaciones de ingeniería , topografía y navegación . 

SISTEMA SEXAGESIMAL O INGLÉS (S)

Es el sistema más utilizado en las aplicaciones de ingeniería , navegación , etc. 

Es aquel sistema cuya unidad de medida es el grado sexagesimal (1°) , el cual resulta de dividir el ángulo de una vuelta en 360 partes iguales. 

Unidad : 1°...(grado sexagesimal), tal que:

Sub unidades : 

1°=60' …(1’ : minuto sexagesimal) 

1'=60''...(1” : segundo sexagesimal) 

En consecuencia : 1°=3600'' 

Además debemos tomar en cuenta que : 

EJEMPLO :

28° 60' 3'' = 28° + 60' + 3''

OBSERVACIÓN 

Los ángulos se miden en grados, minutos y segundos sexagesimales. 

El grado sexagesimal es el ángulo que se obtiene al dividir la circunferencia en 360 partes iguales. 

• Un grado sexagesimal tiene 60 minutos: 1° = 60' 

• Un minuto sexagesimal tiene 60 segundos: 1' = 60" 

EJERCICIOS:

EQUIVALENCIAS:

REGLA DE CONVERSIÓN:

SISTEMA CENTESIMAL O FRANCÉS (C)

Sistema cuya unidad de medida es el grado centesimal (1^g) , el cual resulta de dividir el ángulo de una vuelta en 400 partes iguales .Este sistema es de poco o nula aplicación práctica. 

Unidad : 1^g (grado centesimal), tal que:

Sub unidades :

1^g=100^m...(1^m : minuto centesimal) 

1^m=100^s...(1^s: segundo centesimal) 

En consecuencia : 1^g=10000^s 

NOTA: 

El grado centesimal admite como submúltiplos el minuto y el segundo centesimales. El minuto centesimal es la centésima parte del grado centesimal y el segundo centesimal es la centésima parte del minuto centesimal. 

Este sistema, que tiene la ventaja de que los múltiplos y submúltiplos están vinculados por potencias de 10, pretendió reemplazar al sexagesimal, pero no consiguió imponerse dado que la casi totalidad de los aparatos para medición de ángulos: sextantes, teodolitos, brújulas, etc., están graduados según el sistema sexagesimal.

GRADO CENTESIMAL

Cada una de las porciones que se consiguen al dividir el ángulo recto en 100 partes iguales . 

En el sistema centesimal , la circunferencia se divide en 400^g , cada grado se divide en 100 minutos y cada minuto en 100 segundos . Los segundos se dividen a su vez en décimas , centésimas , milésimas ... Los grados centesimales se designan añadiendo el superíndice « g » a los grados ,« m » a los minutos y , « s » a los segundos . 

12^g35^m47,08^s= 12 grados , 35 minutos , 47,08 segundos.

Además debemos considerar que: 

SISTEMA RADIAL O CIRCULAR (R)

Llamado también internacional, el cual es un sistema cuya unidad de medida es el radián (1rad) el cual representa la amplitud de un arco , en donde su longitud mide igual al radio de la circunferencia que lo contiene . 

La medida de un ángulo en radianes (número de radianes) viene expresado por : 

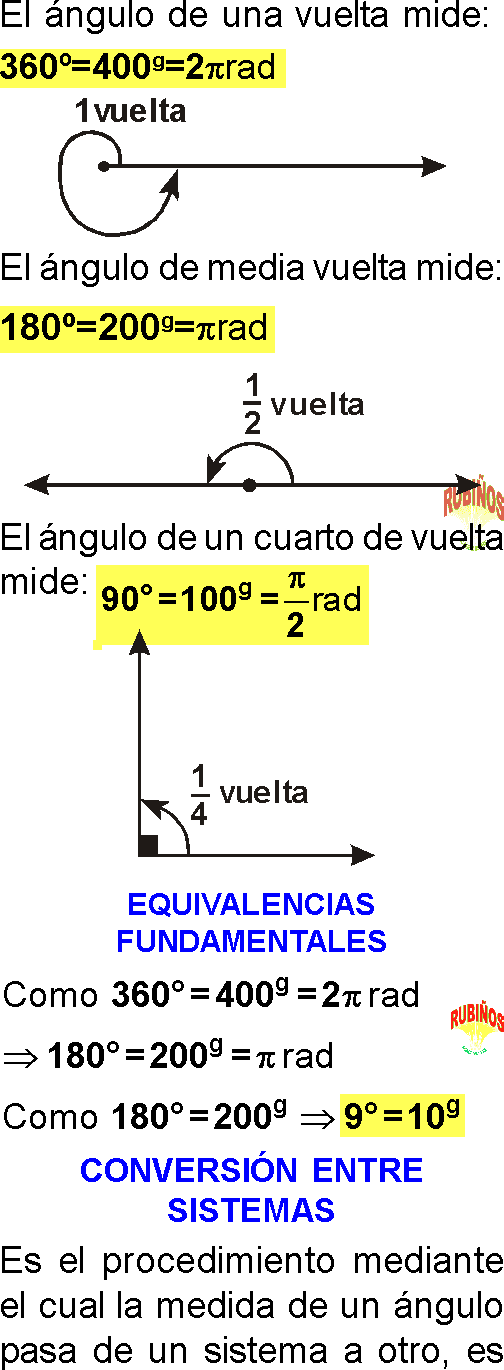
El ángulo de una vuelta mide : 

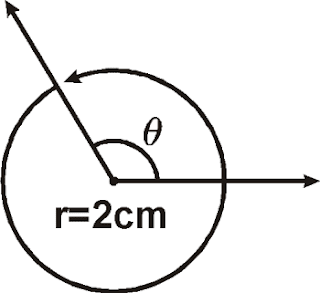
EJEMPLO :

De la definición : 

θ = ℓ/r = 4cm/2cm = 2

El número 2 no tiene unidades , así un ángulo de 2 (radianes) significa un ángulo que subtiende de un arco cuya longitud es dos veces la longitud del radio . (ℓ=2r)

OBSERVACIÓN: 

EQUIVALENCIAS FUNDAMENTALES

Usualmente en el lenguaje matemático no se escribe “radianes” pues ya se sobre entiende, por ejemplo , se escribe sen(𝛑/3) en lugar de sen(𝛑/3rad). 

FACTORES DE CONVERSIÓN 

Son fracciones equivalente a la unidad y se obtienen dividiendo dos cantidades equivalentes , colocando en el numerador una medida en la unidad deseada y en el denominador se coloca su equivalente en la unidad a eliminar . 

MAGNITUDES ANGULARES EQUIVALENTES

Para convertir un ángulo de un sistema otro , multiplicaremos por el factor de conversión. 

EJEMPLO 1: 

Convertir a radianes la siguiente magnitud angular α=12° 

RESOLUCIÓN : 

EJEMPLO 2:

Convertir a radianes la siguiente magnitud angular β=15^g 

RESOLUCIÓN : 

EJEMPLO 3:

Convertir a sexagesimales la siguiente magnitud angular θ=24^g

RESOLUCIÓN :

EJEMPLO 4:

Convertir 36° a radianes. 

RESOLUCIÓN :

EJEMPLO 5:

Convertir 90^g a radianes. 

RESOLUCIÓN : 

EJEMPLO 6:

Convertir a radianes y sexagesimales la magnitud 80^g

RESOLUCIÓN :

EJEMPLO 7:

Calcular:

RESOLUCIÓN :

EJEMPLO 8:

Calcular a+b sabiendo que : (𝛑/8)rad=a°b' 

RESOLUCIÓN :

CONVERSIÓN ENTRE SISTEMAS (OTRA FORMA)

Es el procedimiento mediante el cual la medida de un ángulo pasa de un sistema a otro, es decir, cambiamos su unidad. Para convertir un ángulo “a” en un sistema dado a otro sistema, se tiene que multiplicar por un factor de la forma: 

donde “x” e “y” son cantidades equivalentes. 

Para convertir un ángulo “a” en un sistema dado, a otro sistema, se tiene que multiplicar por un factor de la forma: 

Donde “x” e “y” son equivalentes. 

EJEMPLO 1:

Convertir 60° a radianes 

RESOLUCIÓN :

EJEMPLO 2:

Convertir 45° a radianes. 

RESOLUCIÓN :

EJEMPLO 3:

Convertir 40^g a radianes 

RESOLUCIÓN : 

EJEMPLO 4:

Convertir 72° a centesimales 

RESOLUCIÓN :

OBSERVACIÓN: 

Cuando se operan (suma o resta) ángulos expresados en grados, minutos o segundos en un mismo sistema; se operan independientemente; primero grados, luego minutos y después segundos, para finalmente simplificar. 

Por ejemplo, reducir: 

EJERCICIOS RESUELTOS

EJERCICIO 1 : 

Efectúa: 

A) 2,0 

B) 2,5 

C) 1,0 

D) 3,0 

E) 2,4 

RESOLUCIÓN :

Rpta. : "A"

EJERCICIO 2 : 

En el cuadro siguiente, unir mediante flechas. 

A) IB, IID, IIIF 

B) IC, IID, IIIB 

C) ID, IIA, IIIC 

D) IB, IIC, IIID 

RESOLUCIÓN :

Rpta. : "A"

EJERCICIO 3 : 

Convertir : 5𝛑/32 rad a grados sexagesimales 

A) 28º 5’ 30” 

B) 27º 7’ 30” 

C) 28º 7’ 30” 

D) 27º 6’ 30” 

RESOLUCIÓN :

Rpta. : "C"

EJERCICIO 4 : 

Sabiendo que 

x + y=66° 

x − y= 𝛑/30 rad 

halle el mayor de los ángulos. 

A) 𝛑/5 rad 

B) 𝛑/4 rad 

C) 𝛑/10 rad 

D) 𝛑/9 rad 

RESOLUCIÓN :

Rpta. : "A"

EJERCICIO 5 : 

Se tienen dos ángulos que sumados son 5𝛑/4 rad y su diferencia es 75°. Determina el suplemento del mayor de los ángulos en radianes. 

A) 𝛑/12 rad

B) 𝛑/6 rad 

C) 𝛑/4 rad 

D) 𝛑/3 rad 

RESOLUCIÓN :

Rpta. : "B"

PROBLEMAS RESUELTOS

PREGUNTA 1 :

I) Convertir 36° a grados centesimales. 

II) Convertir 15° a (rad)

III) Convertir 80^g a (rad)

RESOLUCIÓN :

PREGUNTA 2 : 

Señale el valor de: 

A) 1 

B) 1/2 

C) 1/4 

D) 1/3 

E) 2/3 

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 3 : 

Simplificar:

A) 60 

B) 61 

C) 62 

D) 64 

E) 63 

RESOLUCIÓN :

Tenemos que expresar en una misma unidad (minutos). 

Recordar: 

1º=60' ⇒ 2º=120' 

Luego: 

A = (120'+2')/2' = 122'/2'=61

Rpta. : "B"

PREGUNTA 4 :  

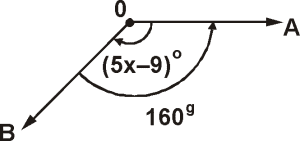
Del gráfico mostrado, calcular "x"

A) 26

B) 25

C) –24

D) –27

E) –17

RESOLUCIÓN : 

Del gráfico: 

(5x–9)º = –160^g

Rpta. : "D"

PREGUNTA 5 :  

Cuántos segundos hay en : 

β=2º4'5''

A) 7444 

B) 7445 

C) 7446 

D) 7404 

E) 7448 

RESOLUCIÓN :

Pasaremos a la misma unidad: 

β = 2º + 4' + 5''

Recordar: 

1º = 3600'' ⇒ 2º = 7200'' 

1' = 60'' ⇒ 4' = 240'' 

Luego: 

β = 7200'' + 240'' + 5'' ⇒ β=7445'' 

Rpta. : "B"

PREGUNTA 6 : 

¿A cuánto equivale 1/5 del ángulo de una vuelta en cada sistema?

A) 30º ; 50^g ; (𝛑/5)rad

B) 60º ; 70^g ; (3𝛑/5)rad

C) 72º ; 80^g ; (2𝛑/5)rad

D) 64º ; 70^g ; (𝛑/5)rad

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 7 : 

Del gráfico, calcular “x”, si OC es bisectriz. 

A) 17 

B) 14 

C) 16 

D) 12 

E) 8 

RESOLUCIÓN : 

Colocando los ángulos en sentido antihorario; como OC es bisectriz, entonces:

Rpta. : "A"

PREGUNTA 8 : 

En un triángulo, dos de sus ángulos miden (𝛑/3)rad y (𝛑/5)rad. ¿Cuál es la medida sexagesimal del tercer ángulo? 

A) 84º 

B) 74º 

C) 94º 

D) 64º 

E) 54º 

RESOLUCIÓN :

Graficando; se nota que sólo debemos sumar los ángulos e igualar dicha suma a 180º. Pero primero convertimos toda al sistema sexagesimal.

Rpta. : "A"

PREGUNTA 9 :  

Señale el valor de:

A) 1 

B) 2 

C) 3 

D) 4 

E) 6 

RESOLUCIÓN : 

Como los ángulos están en unidades diferentes; los vamos a expresar en las mismas unidades para poder operarlos. Todo lo convertimos al sistema sexagesimal; sea: 

Rpta. : "B"

PREGUNTA 10 :  

Del triángulo mostrado, calcular la medida del ángulo “B” en radianes.

A) (𝛑/3)rad

B) (𝛑/4)rad

C) (𝛑/2)rad

D) (𝛑/9)rad

E) (𝛑/7)rad

RESOLUCIÓN : 

Transformando todos los ángulos al sistema sexagesimal : 

Rpta. : "C"

PREGUNTA 11 : 

En un triángulo rectángulo, los ángulos agudos miden (40n)^g y (24n)º. ¿Cuál es el valor de "n"?. 

A) 1 

B) 2 

C) 3 

D) 1/2

E) 3/2 

RESOLUCIÓN :

Graficando la situación; note que para poder operar los ángulos deben estar en las mismas unidades. Convirtiendo: 

Rpta. : "E"

PREGUNTA 12 :  

Determine el valor de la sumatoria infinita siguiente:

A) 600º 

B) 615º 

C) 630º 

D) 645º 

E) 660º 

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 13 : 

En un triángulo ABC se cumple que: 

A + B = (3𝛑/4)rad 

B + C = 135º

Dicho triángulo es: 

A) Equilátero 

B) Escaleno – rectángulo 

C) Isósceles – rectángulo 

D) Obtusángulo 

RESOLUCIÓN :

Rpta. : "C" 

PREGUNTA 14 : 

Calcular "x", en la igualdad:

A) 1

B) 2

C) 3

D) 1/3

E) 1/2

RESOLUCIÓN :

Para poder operar, convertimos todos al sistema sexagesimal ; sea:

Rpta. : "E"

PREGUNTA 15 :  

Simplificar : 

C = (3º4')/4'

A) 36 

B) 46 

C) 56 

D) 66 

E) 76 

RESOLUCIÓN :

Rpta. : "B" 

PREGUNTA 16 :  

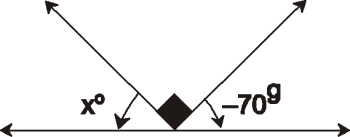
En el gráfico; hallar "x"

A) 17

B) 13

C) 27

D) 23

E) 43

RESOLUCIÓN :

Colocando todos los ángulos en sentido antihorario y convirtiendo al sistema sexagesimal:

Luego : 

70ᵍ + xº = 90º

⇒ 63º + xº = 90º ⇒ xº = 27º ⇒ x=27

Rpta. : "C"

PREGUNTA 17 : 

¿Cuántos minutos centesimales hay en : 

θ=3^g 45^m ?. 

A) 45 

B) 245

C) 145 

D) 345 

E) 445 

RESOLUCIÓN :

Convertimos todos a minutos: 

θ = 3^g 45^m = 3^g + 45^m

Como : 

1^g= 100^m ⇒ 3^g = 300^m

Luego : 

θ = 300^m + 45^m =345^m

Rpta. : "D"

PREGUNTA 18 : 

Sabiendo que un ángulo se expresa como (7n+1)° y también como (8n)^g. 

¿Cuál es su medida radial?. 

A) (𝛑/3)rad

B) (𝛑/4)rad

C) (𝛑/5)rad

D) (𝛑/6)rad

E) (𝛑/9)rad

RESOLUCIÓN :

Sea “α” el ángulo ; luego : α=(7n+1)° y α = (8n)^g

Pero para poder igualar y operar , lo expresamos en la misma unidades: 

Rpta. : "C"

PREGUNTA 19 : 

En un triángulo isósceles, los ángulos miden (7n – 2)° y (7n + 4)^g

¿Cuántos mide el ángulo desigual en el sistema sexagesimal?. 

A) 60° 

B) 44° 

C) 36° 

D) 72° 

E) 54° 

RESOLUCIÓN :

Graficando ; tenemos: A=(7n–2)° y C=(7n+4)^g, para poder igualar convertimos : 

Ahora si; igualando : A=C 

Rpta. : "D"

PREGUNTA 20 :  

Las medidas de los tres ángulos de un triángulo son: (9x/10)°, (x+1)rad y (x+2)^g

El mayor de ellos expresado en radianes es: 

RESOLUCIÓN :

Rpta. : "B"

GUÍA DE CLASE

PREGUNTA 1 :

Complete : 

"En el sistema sexagesimal su unidad es un grado sexagesimal, que se denota por ........................ y en el sistema radial su unidad es un radián denotado por .........................".

PREGUNTA 2 :

Asocie mediante flechas: 

PREGUNTA 3 :

Exprese 140^g – (2𝛑/5)rad en el sistema sexagesimal. 

PREGUNTA 4 :

Convertir 20° al sistema circular. 

A) (𝛑/9)rad

B) (𝛑/10)rad

C) (𝛑/7)rad

D) (𝛑/20)rad

E) (2𝛑/5)rad

PREGUNTA 5 :

Calcular: (2°3')/3'

PREGUNTA 6 :

Expresar 40° en el sistema circular. 

A) (𝛑/10)rad

B) (𝛑/40)rad

C) (𝛑/9)rad

D) (2𝛑/9)rad

E) (𝛑/18)rad

PREGUNTA 7 :

Exprese 50° en el sistema circular. 

A) (5𝛑/18)rad

B) (2𝛑/9)rad

C) (2𝛑/5)rad

D) (𝛑/5)rad

E) (𝛑/3)rad

PREGUNTA 8 :

Convertir 18° al sistema circular. 

A) (𝛑/9)rad

B) (𝛑/10)rad

C) (𝛑/7)rad

D) (𝛑/20)rad

E) (2𝛑/5)rad

PREGUNTA 9 :

Convertir 80^g al sistema radial. 

A) (4𝛑/3)rad

B) (4𝛑/9)rad

C) (4𝛑/5)rad

D) (2𝛑/5)rad

E) (3𝛑/5)rad

PREGUNTA 10 :

Convertir 100^g al sistema sexagesimal. 

A) 190º 

B) 130º

C) 140º 

D) 90º 

E) 100º 

PREGUNTA 11 :

Calcular: M = (𝛑/3)rad + 50^g en el sistema sexagesimal. 

A) 107º 

B) 105º 

C) 115º 

D) 110º 

E) 125º 

PREGUNTA 12 :

Convertir (3𝛑/20)rad al sistema sexagesimal. 

A) 25º 

B) 27º 

C) 28º 

D) 26º 

E) 30º 

PREGUNTA 13 :

Convertir (𝛑/10)rad al sistema centesimal. 

A) 20^g 

B) 30^g

C) 18^g 

D) 10^g

E) 15^g 

PREGUNTA 14 :

¿Cuántos segundos sexagesimales hay en 5º4'32''? 

A) 18270''

B) 18271'' 

C) 18272'' 

D) 18200'' 

E) 18371''

PREGUNTA 15 :

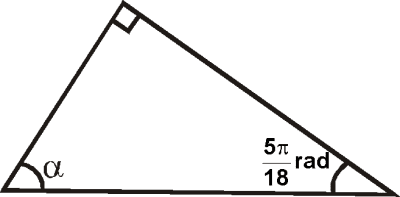
Calcule α en radianes. 

A) (𝛑/18)rad

B) (5𝛑/36)rad

C) (5𝛑/18)rad

D) (5𝛑/12)rad

E) (𝛑/3)rad

PREGUNTA 16 :

Convierte a radianes 68º+32º

A) (5𝛑/9)rad

B) (2𝛑/5)rad

C) (3𝛑/8)rad

D) (5𝛑/12)rad

E) (𝛑/2)rad

PREGUNTA 17 :

Convierte a sexagesimales: 

(𝛑/9)rad + (𝛑/6)rad

A) 48º 

B) 60º 

C) 80º 

D) 50º 

E) 72º 

PREGUNTA 18 :

Calcular: 

A) 5 

B) 4 

C) 3 

D) 7 

E) 6 

PREGUNTA 19 :

Calcule ‘‘α’’ en sexagesimales 

A) 80º 

B) 72º 

C) 60º 

D) 75º 

E) 70º 

PREGUNTA 20 :

Calcule ‘‘α’’ en radianes

A) (4𝛑/9)rad

B) (3𝛑/5)rad

C) (2𝛑/9)rad

D) (𝛑/6)rad

E) (𝛑/5)rad

• CLIC AQUÍ Ver PDF