ÁNGULO TRIGONOMÉTRICO EJERCICIOS RESUELTOS PDF
Se tienen desniveles en el terreno, y con la ayuda de la topografía se encuentran ángulos que luego sirven para planos horizontales en la construcción civil.
Asimismo, en lo que respecta a la recreación, se tiene deportes como el windsurfing en el que se hace uso del ángulo óptimo de estabilidad en la tabla para resistir no solo a las olas, sino inclusive a la fuerza del viento que arrecia sobre la vela.
De igual modo, los aviones, cohetes, balas tienen un ángulo de salida para llegar al destino, los ingenieros hacen los cálculos necesarios para encontrar el ángulo adecuado.
Los ángulos pueden ser medidos con una regla graduada llamada transportador.
• Entender el porqué de la diferencia entre el ángulo definido en geometría y trigonometría (el ángulo generado por la rotación de un rayo alrededor de un punto fijo (vértice), todo ello en un mismo plano).
• Reconocer la características fundamentales de los ángulos trigonométricos en cuanto a su generación y tipo de rotación: horario y antihorario.
A través de la historia los avances que se producen en todos los campos de la ciencia son el producto de satisfacer las necesidades.
La trigonometría no es ajena a este proceso y establece una definición de ángulo diferente a la definición clásica planteada en geometría «intersección de dos rayos con un vértice común».
Con el objeto de introducir en nuestro campo de estudio a los ángulos mayores a una vuelta, así como también, luego de establecer alguna conversión de ángulos en el plano generadas en un sentido u otro (diferencias en el signo).
GENERACIÓN Y CARACTERÍSTICAS DEL ÁNGULO TRIGONOMÉTRICO
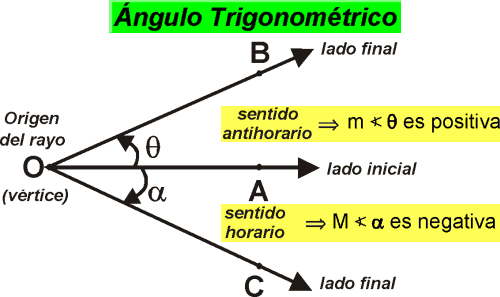
Es aquel que se genera por la rotación de un rayo (en un mismo plano), alrededor de un punto fijo llamado vértice, desde una posición inicial hasta una posición final. Consideramos un ángulo positivo cuando la rotación del rayo sea contraria al movimiento de las manecillas de un reloj (antihorario); cuando la rotación sea en el mismo sentido del movimiento (horario), el ángulo se considera negativo.
Los ángulos trigonométricos serán medidos en tres sistemas que estudiaremos a continuación, pero es bueno mencionar una convención a cerca de la rotación que genera un ángulo trigonométrico y su medida.
EJEMPLO :
Nótese en la figura:
“θ” es un ángulo trigonométrico de medidas positiva.
“x” es un ángulo trigonométrico de una medida negativa.
⇒ Se cumple : x = – θ
ÁNGULO NULO :
Si el rayo no gira, la medida del ángulo será cero.
ÁNGULO DE UNA VUELTA :
Se genera por la rotación completa de un rayo, es decir su lado final coincide con su lado inicial por primera vez.
MEDICIÓN DE UN ÁNGULO
Cuando medimos un ángulo , tratamos de asignarle un número que indique la magnitud de este . Se debe tener presente para un ángulo positivo , que cuando sea mayor la rotación , mayor será el ángulo.
ÁNGULO DE UNA VUELTA
Es aquel que se genera, cuando el lado final e inicial coinciden por primera vez luego de cierta rotación. Podríamos asignarle a este ángulo el número 1 y decir que ángulo de una vuelta es: 1v.
La forma más lógica para medir el ángulo es el número de vueltas o llamado también número de revoluciones, así podemos obtener de manera natural los ángulos y sus asignaciones numéricas, como se muestra en la figura.
CARACTERÍSTICAS
I) La medida del ángulo trigonométrico no se encuentra sujeto a restricciones pudiendo ser un ángulo de cualquier magnitud.
EJEMPLO :
En la figura (1), el ángulo trigonométrico mide “3 vueltas”, en la figura (2) el ángulo trigonométrico mide “– 2 vueltas”.
II) Si se cambia el sentido de la rotación de un ángulo, entonces su medida cambiará de signo.
EJEMPLO :
Se recomienda colocar todos los ángulos en sentido antihorario.
Para realizar operaciones con ángulos trigonométricos estos deberán estar en el mismo sentido.
Por ejemplo , de la figura se tiene :
PROBLEMAS RESUELTOS
PREGUNTA 1 :
Hallar “x”, en función de “θ” y “β”.
.png)
RESOLUCIÓN :
Se nota que “x” está en sentido antihorario, es conveniente tener a los ángulos en un mismo sentido.
.png)
Rpta. : "B"
PREGUNTA 2 :
Del gráfico siguiente:
Indicar cuál(es) de las proposiciones son verdaderas (V) o falsa (F):
I) Es α = θ
II) α + β = 180°
III) θ es un ángulo positivo y α es un ángulo negativo
a) VVF
b) VFF
c) VFV
d) FFV
RESOLUCIÓN :
Para relacionar ángulos trigonométricos estos deben de tener el mismo sentido.
Luego, en el gráfico:
.png)
I) Falsa , puesto que: –α = θ
II) Falsa , puesto que: –α + β = 180°
III) Verdadera , puesto que θ tiene sentido antihorario y α sentido horario .
Rpta. : "D"
PREGUNTA 3 :
Interpretar “x” en función de
.png)
RESOLUCIÓN :
En primer lugar se debe tratar que los ángulos presentes aparezcan en el mismo sentido, de preferencia sentido antihorario. Por lo tanto el gráfico queda así:
.png)
Rpta. : "B"
PREGUNTA 4 :
Del gráfico, se cumple:
.png)
RESOLUCIÓN :
.png)
Rpta. : "B"
PREGUNTA 5 : :
Calcular “x” en función de “α”, “β” y “θ”.
.png)
RESOLUCIÓN :
Note que “x” está en sentido horario, entonces cambiamos al mismo sentido.
x = (– θ) + β + (– α)
Ordenando: x = β – θ – α
Rpta. : "B"
PREGUNTA 6 :
Calcular “x” en función de “α”, “β” y “θ”.
.png)
Según las recomendaciones anteriores, trataremos de colocar los ángulos en sentido antihorario.
.png)
Rpta. : "B"
PREGUNTA 7 :
Hallar: “x”
.png)
a) – 90º
b) –190º
c) – 196º
d) – 80º
e) – 180º
RESOLUCIÓN :
Colocando en un mismo sentido:
.png)
Del gráfico:
230º + 320º – (– x) = 360º
⇒ x = –190º
Rpta. : "B"
PREGUNTA 8 : :
Indicar la relación que se cumple entre “Φ” y “β”
.png)
RESOLUCIÓN :
Ordenando el gráfico :
.png)
Rpta. : "B"
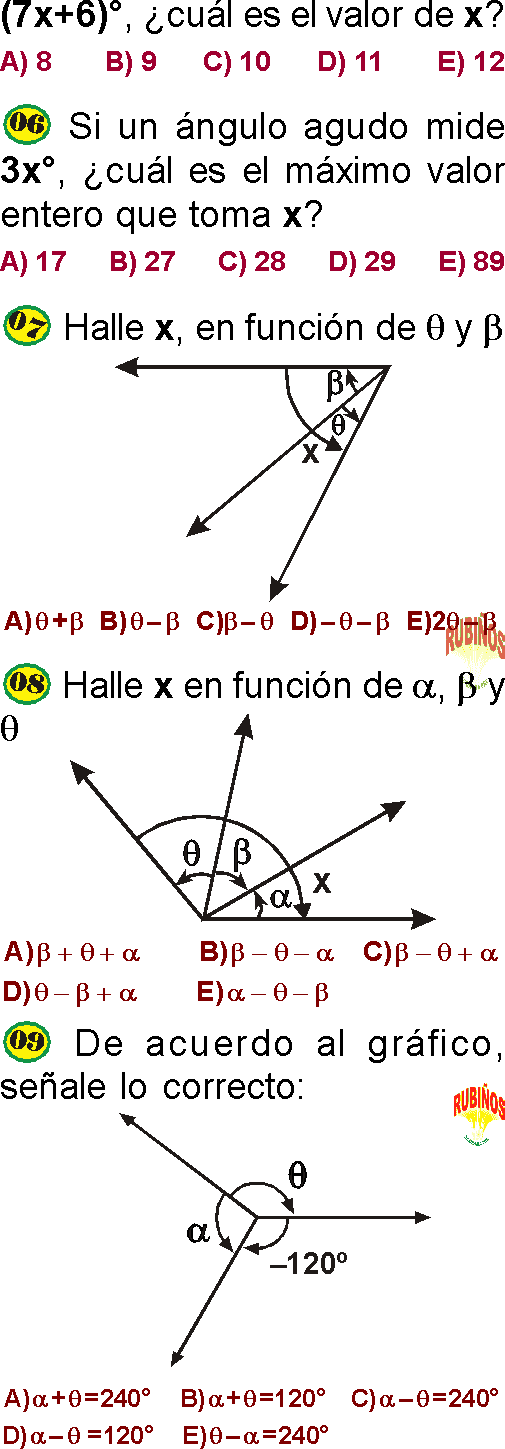
PREGUNTA 9 :
Calcular “x”.
.png)
A) 30°
B) –30°
C) 15°
D) 10°
E) –10°
RESOLUCIÓN :
Colocando en un mismo sentido :
.png)
De la figura :
3x+30°+90°+6x – 30°=180° ⇒ x=10°
Rpta. : "D"
PREGUNTA 10 :
El gráfico mostrado, indicar la relación que existe entre “α”, “β” y “θ”
.png)
RESOLUCIÓN :
Replanteando el gráfico a nuestra conveniencia :
.png)
Por lo tanto : β – α – θ = 180°
Rpta. : "C"
PREGUNTA 11 :
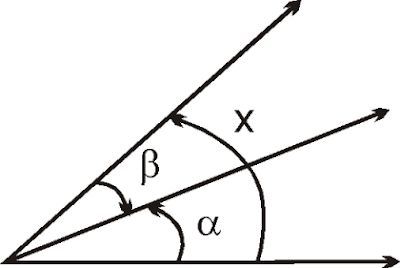
Calcular “x”, en función de “α” y “β”
.png)
RESOLUCIÓN :
Como “x” está en sentido antihorario ; vamos a procurar que todos los ángulos aparezcan en el mismo sentido ; para ello sólo cambiamos “β” ; quedando :
.png)
Rpta. : "B"
PREGUNTA 12 :
En el gráfico mostrado, ¿Cuál es el valor de “x”?
.png)
RESOLUCIÓN :
Graficando adecuadamente :
.png)
Rpta. : "D"
PREGUNTA 13 :
Calcular “x” del gráfico :
.png)
RESOLUCIÓN :
Colocando todos los ángulos en sentido antihorario ; tenemos:
.png)
Rpta. : "C"
PREGUNTA 14 :
Halle “x” en función de “α”, “β” y “θ”.
.png)
A) β + θ + α
B) β – θ – α
C) – θ + α
D) θ – β + α
E) α – θ + β
RESOLUCIÓN :
Note que el ángulo pedido está en sentido horario , así que vamos a colocar todo en dicho sentido ; así:
.png)
x = (– θ) + β + (– α)
Ordenando: x = β – θ – α
Rpta. : "B"
PREGUNTA 15 :
Del gráfico , se cumple :
.png)
RESOLUCIÓN :
Colocando todo en sentido antihorario :
.png)
Ordenando : β – α = 1/2 vuelta
Rpta. : "C"
PREGUNTA 16 :
Del gráfico , se cumple :
.png)
RESOLUCIÓN :
Del gráfico , colocamos todas las rotaciones en sentido antihorario :
.png)
Rpta. : "B"
PREGUNTA 17 :
Del gráfico mostrado calcular el valor de verdad de las siguientes proposiciones:
.png)
A) VVF
B) FFF
C) FFV
D) VFV
E) VVV
RESOLUCIÓN :
Colocando en un solo sentido :
.png)
Por lo tanto : I) F ; II) F y III) V
Rpta. : "C"
PREGUNTA 18 :
En el gráfico mostrado ¿Cuál es el valor de “x” ?
.png)
RESOLUCIÓN :
De la figura:
.png)
Rpta. : "C"
PREGUNTA 19 :
En el gráfico mostrado. calcular “x”.
.png)
RESOLUCIÓN :
.png)
Rpta. : "D"
PREGUNTA 20 :
En el gráfico mostrado, calcular “x”.
.png)
RESOLUCIÓN :
De la figura :
.png)
Rpta. : "C"
GUÍA DE CLASE
PREGUNTA 1 : Complete en cada recuadro el sentido de la rotación en que fue generado cada ángulo.
De acuerdo al gráfico, señale la relación que verifican “α” , “β” y “θ”.
Asocie mediante flechas:
En cada caso, tomando como inicio de giro el rayo OP, dibuje un ángulo en sentido:
PREGUNTA 5 :
En cada caso, tomando como inicio de giro el rayo OP, dibuje un ángulo en sentido:
PREGUNTA 6 :
En cada caso, tomando como inicio de giro al rayo OP, dibuje un ángulo (use transportador) que mida:
PREGUNTA 7 :
En cada caso, tomando como inicio de giro al rayo OP, dibuje un ángulo (use transportador) que mida:
PREGUNTA 8 :
Tomando como inicio de giro (lado inicial) el rayo indicado, dibuje un ángulo que mida:
En cada caso, hallar “x”, en función de los ángulos mostrados.
PREGUNTA 9 :
PREGUNTA 10 :
PREGUNTA 11 :
PREGUNTA 12 :
PREGUNTA 13 :
PREGUNTA 14 :
Del gráfico, hallar "x".
PREGUNTA 15 :
Del gráfico, hallar "x".
PREGUNTA 16 :
Hallar "x", si:
PREGUNTA 17 :
Hallar "x", si:
PREGUNTA 18 :
Hallar "x", si:
PREGUNTA 19 :
Hallar "x", si:
PREGUNTA 20 :
Hallar "x", si:
GUÍA DE CLASE II
PREGUNTA 1 :
Hallar “x”. Si L₁//L₂
A) 30º
B) 40º
C) 60º
D) 45º
E) 50º
PREGUNTA 2 :
Si un ángulo recto mide (5x + 20)°, ¿Cuál es el valor de “x”?
A) 12
B) 14
C) 26
D) 30
E) 32
PREGUNTA 3 :
Si un ángulo agudo mide (3x – 12)°, ¿Cuál es el máximo valor entero que puede tomar “x”?
A) 30
B) 31
C) 32
D) 33
E) 34
PREGUNTA 4 :
Calcular: “θ + α”
A) 90º
B) 180º
C) 270º
D) 135º
E) 150º
PREGUNTA 5 :
En el gráfico, OM es bisectriz del AOB. ¿Cuál es el valor de “x”?
A) 1
B) 2
C) 3
D) 4
E) 5
PREGUNTA 6 :
Del gráfico, señale lo correcto:
A) x + y = 90º
B) x – y = 300º
C) x + y = 270º
D) x – y = 270º
E) x – y = 180º
PREGUNTA 7 :
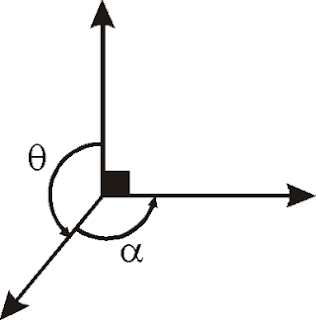
De acuerdo al gráfico, señale lo correcto:
A) x + y = 180º
B) x + y = 360º
C) x – y = 360º
D) x – y = 180º
E) x – y = 270º
PREGUNTA 8 :
Del gráfico, señale lo correcto:
A) x – y = 180º
B) x + y = 180º
C) x – y = 300º
D) x + y = 300º
E) x – y = 450º
PREGUNTA 9 :
Si un ángulo “θ” agudo, mide:
(6x + 18)°, ¿Cuál es el máximo valor entero que puede tomar “x”?
A) 10
B) 11
C) 12
D) 13
PREGUNTA 10 :
Si un ángulo obtuso mide:
(6x + 120)°, ¿Cuál es el máximo valor entero que puede tomar “x”?
A) 7
B) 8
C) 9
D) 10
E) 11
PREGUNTA 11 :
Si un ángulo obtuso mide: (4n + 60)°, ¿Cuál es el máximo valor entero que puede tomar “n”?
A) 27
B) 28
C) 29
D) 30
E) 31
PREGUNTA 12 :
Si un ángulo agudo mide: (3n + 24)°, ¿Cuál es el máximo valor entero que puede tomar “n”?
A) 20
B) 21
C) 22
D) 23
E) 24
PROBLEMAS PROPUESTOS CON RESPUESTAS AL FINAL
PREGUNTA 1 :
Hallar “x”, en función de “θ” y “β”.
PREGUNTA 2 :
Del gráfico siguiente:
.png)
Indicar cuál(es) de las proposiciones son verdaderas (V) o falsa (F):
I) Es α = θ
II) α + β = 180°
III) θ es un ángulo positivo y α es un ángulo negativo
A) VVF
B) VFF
C) VFV
D) FFV
PREGUNTA 3 :
Interpretar “x” en función de
PREGUNTA 4 :
Del gráfico, se cumple:
PREGUNTA 5 : :
Calcular “x” en función de “α”, “β” y “θ”.
PREGUNTA 6 :
Calcular “x” en función de “α”, “β” y “θ”.
PREGUNTA 7 :
Hallar: “x” .png)
A) – 90º
B) –190º
C) – 196º
D) – 80º
E) – 180º
PREGUNTA 8 : :
Indicar la relación que se cumple entre “Φ” y “β”
PREGUNTA 9 :
Calcular “x”.
A) 30°
B) –30°
C) 15°
D) 10°
E) –10°
PREGUNTA 10 :
El gráfico mostrado, indicar la relación que existe entre “α”, “β” y “θ”
PREGUNTA 11 :
Calcular “x”, en función de “α” y “β”
PREGUNTA 12 :
En el gráfico mostrado, ¿Cuál es el valor de “x”?
PREGUNTA 13 :
Calcular “x” del gráfico :
PREGUNTA 14 :
Halle “x” en función de “α”, “β” y “θ”.
A) β + θ + α
B) β – θ – α
C) – θ + α
D) θ – β + α
E) α – θ + β
PREGUNTA 15 :
Del gráfico , se cumple :
PREGUNTA 16 :
Del gráfico , se cumple :
PREGUNTA 17 :
Del gráfico mostrado calcular el valor de verdad de las siguientes proposiciones:
A) VVF
B) FFF
C) FFV
D) VFV
E) VVV
PREGUNTA 18 :
En el gráfico mostrado ¿Cuál es el valor de “x” ?
PREGUNTA 19 :
En el gráfico mostrado. calcular “x”.
PREGUNTA 20 :
En el gráfico mostrado, calcular “x”.
CLAVES – RESPUESTAS : 1)B 2)D 3)B 4)B 5)B 6)B 7)B 8)B 9)D 10)C 11)B 12)D 13)C 14)B 15)C 16)B 17)C 18)C 19)D 20)C
“LOS ANTIGUOS Y LA TRIGONOMETRÍA”
La Trigonometría como cualquier otra rama de la Matemática fue desarrollada por célebres matemáticos a través del tiempo, desde los egipcios pasando por los hindúes quienes introducen los conceptos de funciones de un ángulo (Seno) y conceden la importancia del arco que tiene igual longitud del radio de la circunferencia que los contiene hasta los célebres F. Viete (1540 - 1603), L. Euler (1707 - 1783), entre otros.
Ya Euclides en su famosa obra “Elementos”, presenta teoremas relativos a la razón entre los lados de un triángulo rectángulo y problemas conceptos referente al teorema de cosenos en un triángulo obtusángulo.
Aristarco de Samos midió el ángulo entre la visual dirigida al Sol y la visual dirigida a la Luna y descubrió que el ángulo es menor en 1/30 de un cuadrante, lo cual significa que la razón entre la distancia de la Tierra a la Luna, y de la Tierra al Sol es aproximadamente igual a Sen3º.
Alejandro Ptolomeo (Siglo II) publica su obra “Alma Gesto” es decir “El más grande los libros”; Ptolomeo fundó su Trigonometría sobre un teorema clásico: “El producto de los diagonales de un cuadrilátero inscriptible es igual a la suma de los productos de los lados opuestos”.
Menelao, discípulo de Hiparco escribió un tratado de Trigonometría Esférica que fue estudiado por los árabes.
Eratóstenes fue también otro sabio que desarrolló la trigonometría quien midió la distancia de la Tierra al Sol y de la Tierra a la luna a partir del radio de la Tierra. Y fueron muchos más que permanecen en el anonimato quienes contribuyeron con el desarrollo de la Trigonometría.
