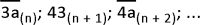SIMULACRO UNI 2024 SEGUNDA PRUEBA DE INGRESO SOLUCIONARIO UNIVERSIDAD DE INGENIERÍA PDF

PREGUNTA 1 : 
Se dispone de tres recipientes cúbicos cuyos lados de longitud L1, L2, L3 cumplen con la siguiente condición: 
Se pretende distribuir 434 litros de agua entre los tres recipientes de modo que alcancen el mismo nivel o altura. Determine los litros de agua que recibe el recipiente de longitud L2. 
A) 112 
B) 120 
C) 124 
D) 136 
E) 146 
PREGUNTA 2 : 
El perímetro de un triángulo es 50 m y sobre cada lado del triángulo se forma un cuadrado cuyo lado coincida con el lado del triángulo. Como resultado, la suma de las áreas de los cuadrados formados es 900m² y el lado del primer cuadrado es al del segundo como, el lado del tercero es a la mitad del primero. La relación del mayor y el menor de los lodos del triángulo es de (Considere que los lados del triángulo son números naturales) 
A) 2 a 1 
B) 5 a 2 
C) 3 a 1 
D) 5 a 1 
E) 11 a 2 
PREGUNTA 3 : 
Las magnitudes X e Y son tales que (Y – 2) y (X²+ 1) son inversamente proporcionales. Se sabe que cuando X=2, se tiene que Y= 3. Determine la ecuación que relaciona X e Y 
PREGUNTA 4 : 
Considere la progresión aritmética 
donde la suma de los tres primeros términos es mayor que 170. Si n es el menor posible, calcule la suma de los primeros 12 términos de esta progresión. 
A) 1150 
B) 1330 
C) 1340 
D) 1350 
E) 1650 
PREGUNTA 5 : 
Indique la secuencia correcta después de determinar si la proposición es verdadera (V) o Falsa (F). 
I. El producto de un número irracional por otro irracional es siempre irracional. 
II. La suma de dos números irracionales siempre es un número irracional. 
III. Entre dos números racionales diferentes siempre existe otro número racional. 
A) VVV 
B) VFV 
C) VFF 
D) FFF 
E) FFV 
PREGUNTA 6 : 
Sea la fracción a/3 (a y 3 primos entre sí), con a > 0. 
Al numerador le agregamos el número A∈ℕ y al denominador 2A, se obtiene una fracción equivalente que es la mitad de la fracción original, entonces la suma de todos los valores posibles de a es: 
A) 4 
B) 8 
C) 9 
D) 12 
E) 15 
PREGUNTA 7 : 
Halle un número de la forma
tal que sea múltiplo de44 
Dar como respuesta el residuo que se obtiene al dividir dicho número entre 5. 
A) 0 
B) 1 
C) 2 
D) 3 
E) 4 
PREGUNTA 8 : 
El número de hijos por familia en una determinada ciudad es una variable aleatoria H, cuya función de probabilidad es
 f(x)=P[H=x]=Kx/5 
x = 1; 2; 3; 4; 5 
¿Cuál es la probabilidad de que una familia tenga 3 hijos dado que tiene al menos dos hijos? 
A) 0,200 
B) 0,333 
C) 0,214 
D) 0,267 
E) 0,357 
PREGUNTA 9 : 
Se elige aleatoriamente un número entero de cinco cifras. Calcule la probabilidad que dicho número sea par y la suma de sus cifras sea 42. 
PREGUNTA 10 : 
PREGUNTA 11 : 
Sean las ecuaciones 
y=x² – 3x+4 
y=mx+3 
Determine los valores reales de m para que nunca se intersequen.
PREGUNTA 12 : 
PREGUNTA 13 : 
PREGUNTA 14 : 
Halle el polinomio p(x) de coeficientes racionales de menor grado con raíces 1 y 1+√2, y que además cumpla p(0) = 1. 
Dé como respuesta la suma de los coeficientes del polinomio. 
A) –2 
B) –1 
C) 0 
D) 1 
E) 3 
PREGUNTA 15 : 
PREGUNTA 16 : 
Calcule: 
Dar como respuesta la primera cifra decimal. 
A) 0 
B) 1 
C) 2 
D) 3 
E) 4
PREGUNTA 17 : 
PREGUNTA 18 : 
Al efectuar la división 
el término independiente del cociente que resulta es 
A) – 2n 
B) – n 
C) 0 
D) n 
E) 2n 
PREGUNTA 19 : 
Determine los puntos de intersección de la gráfica de la función definida por 
f (x) =│x − 2│+ x² con la recta 3x – 2y= – 11. 
A) ( – 1; 2), (3; 9) 
B) (1; – 4), (3; 10) 
C) (–1; 4), (3; 10) 
D) ( – 1; 1), (4; 9) 
E) (1; – 4), (3; 12) 
PREGUNTA 20 : 
PREGUNTA 21 : 
PREGUNTA 22 : 
El cateto AB del triángulo rectángulo ABC se divide en 8 partes congruentes. Por los puntos de división se trazan 7 segmentos paralelos al cateto AC tal como se muestra en la figura. Si AC=10 m, halle la suma (en m) de las longitudes de los 7 segmentos. 
A) 33 
B) 34 
C) 35 
D) 36 
E) 37 
PREGUNTA 23 : 
En el ángulo triedro trirectángulo O - ABC; si las áreas de las caras OAB, OBC y OAC miden
respectivamente 𝕊, 2𝕊 y 3𝕊. Entonces el área de la región que determina un plano secante a las aristas y que pasa A, B y C es
A) 2𝕊√2 
B) 3𝕊√2 
C) 𝕊√14
D) 2𝕊√3 
E) 𝕊√15
PREGUNTA 24 : 
Al cortarse dos cuerdas de una misma circunferencia perpendicularmente, una de ellas queda dividida en segmentos de 3 y 4 unidades y la otra en segmentos de 6 y 2 unidades. Determine el diámetro de la circunferencia. 
A)√87 
B)√73 
C)√68 
D)√65 
E)√63 
PREGUNTA 25 : 
La superficie lateral de un prisma recto regular triangular es un rectángulo cuya diagonal mide 12 m y su altura 6√3 m. Calcule el área total del sólido (en m²). 
A) 38√3 
B) 39√3 
C) 40√3 
D) 41√3 
E) 42√3 
PREGUNTA 26 : 
PREGUNTA 27 : 
En un tronco de pirámide ABC-A1B1C1, los volúmenes de las pirámides B1-ABC y A-A1B1C1, miden V1 y V2 respectivamente. Determine el volumen de la pirámide A-CB1C1.
PREGUNTA 28 : 
PREGUNTA 29 : 
Las caras de un triedro equilátero de vértice V miden 60°. En una de sus aristas se considera un punto R de tal manera que VR=2 cm. Por R pasa un plano perpendicular a VR que interseca a las otras aristas en S y T. Halle el área del triángulo RST (en cm²). 
A) 3√2 
B) 2√6 
C)√26 
D) 3√3 
E) 4√2 
PREGUNTA 30 : 
PREGUNTA 31 : 
PREGUNTA 32 : 
El menor ángulo de un paralelogramo mide a y sus diagonales miden 2m y 2n. Calcule su área. (m>n) 
A) (m² – n²)tan(α) 
B) (m² – n²)cot(α) 
C) (m² – n²)sec(α) 
D) (m² – n²)csc(α) 
E) (m² – n²)sen(α) 
PREGUNTA 33 : 
PREGUNTA 34 : 
Un marino que observa el horizonte desde un faro de altura h, lo hace con un ángulo de depresión θ. Calcule el radio R de la Tierra en función de h y θ. 
PREGUNTA 35 : 
Si la gráfica de y=Aarccos(Bx+C) +D es
determine el valor de E=A+B+C. 
A) 3 
B) 2/3 
C) 4/3 
D) 4 
E) 14/3
PREGUNTA 36 : 
PREGUNTA 37 : 
A) 2cos(θ) – sen(θ) 
B) cos(θ) – sen(θ) 
C) 2sen(θ) – cos(θ) 
D) sen(θ) + cos(θ) 
E) sen(θ) – cos(θ) 
PREGUNTA 38 : 
La ecuación de una cónica en coordenadas polares es
Determine una ecuación cuadrática para sus puntos en coordenadas rectangulares
PREGUNTA 39 : 
PREGUNTA 40 : 
Dada la ecuación general de la cónica : Ax²+By²+Cx+Dy+F=0 con A, B, C, D, F constantes arbitrarias, se tiene que: 
I) Si A=B≠0, entonces siempre tenemos la ecuación de una circunferencia. 
II) Si B=0 y A≠0, entonces siempre tenemos la ecuación de una parábola. 
III) Si A.B<0 y D² – 4BF<0, entonces siempre tenemos la ecuación de una hipérbola. 
Luego son verdaderas: 
A) solo I 
B) II y III 
C) solo II 
D) solo III 
E) I y III
CLAVES-RESPUESTAS : 1)C    2)A    3)C    4)D    5)E    6)A    7)B    8)C    9)B    10)D    11)A     12)A    13)A    14)C    15)A     16)C    17)D    18)B    19)C    20)A    21)A    22)C    23)C    24)D    25)A    26)E     27)A    28)A    29)E    30)C    31)C    32)A    33)A   34)B    35)D  36)B    37)B     38)B    39)D    40)D
SOLUCIONARIO

Ejercicios resueltos de examen de admisión a la Universidad