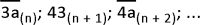ARITMÉTICA UNI RESUELTA DE INGRESO UNIVERSIDAD INGENIERÍA
PREGUNTA 1 :
Se dispone de tres recipientes cúbicos cuyos lados de longitud L1, L2, L3 cumplen con la siguiente condición:
Se pretende distribuir 434 litros de agua entre los tres recipientes de modo que alcancen el mismo nivel o altura. Determine los litros de agua que recibe el recipiente de longitud L2.
A) 112
B) 120
C) 124
D) 136
E) 146
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 2 :
El perímetro de un triángulo es 50 m y sobre cada lado del triángulo se forma un cuadrado cuyo lado coincida con el lado del triángulo. Como resultado, la suma de las áreas de los cuadrados formados es 900 m2 y el lado del primer cuadrado es al del segundo como, el lado del tercero es a la mitad del primero. La relación del mayor y el menor de los lodos del triángulo es de (Considere que los lados del triángulo son números naturales)
A) 2 a 1
B) 5 a 2
C) 3 a 1
D) 5 a 1
E) 11 a 2
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 3 :
Las magnitudes X e Y son tales que (Y–2) y (X2+1) son inversamente proporcionales. Se sabe que cuando X=2, se tiene que Y=3. Determine la ecuación que relaciona X e Y
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 4 :
Considere la progresión aritmética
donde la suma de los tres primeros términos es mayor que 170. Si n es el menor posible, calcule la suma de los primeros 12 términos de esta progresión.
A) 1150
B) 1330
C) 1340
D) 1350
E) 1650
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 5 :
Indique la secuencia correcta después de determinar si la proposición es verdadera (V) o Falsa (F).
I) El producto de un número irracional por otro irracional es siempre irracional.
II) La suma de dos números irracionales siempre es un número irracional.
III) Entre dos números racionales diferentes siempre existe otro número racional.
A) VVV
B) VFV
C) VFF
D) FFF
E) FFV
RESOLUCIÓN :
I) Falso
Veamos un contraejemplo (√3−1) (√3+1)=3−1
irracional×irracional racional
Por lo tanto, el producto de dos números irracionales puede resultar un número racional.
II) Falso
Veamos un contraejemplo (1−√2)+(1−√2)=2
irracional+irracional racional
Por lo tanto, la suma de dos números irracionales puede resultar un número racional.
III) Verdadero
Se sabe que el conjunto de los números racionales es un conjunto denso; es decir, entre dos racionales cualesquiera hay infinitos racionales.
Por lo tanto, entre dos racionales diferentes siempre existe otro números racionales.
Rpta. : "E"
PREGUNTA 6 :
Sea la fracción a/3 (a y 3 primos entre sí), con a > 0.
Al numerador le agregamos el número A∈ℕ y al denominador 2A, se obtiene una fracción equivalente que es la mitad de la fracción original, entonces la suma de todos los valores posibles de a es:
A) 4
B) 8
C) 9
D) 12
E) 15
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 7 :
Halle un número de la forma
tal que sea múltiplo de44
Dar como respuesta el residuo que se obtiene al dividir dicho número entre 5.
A) 0
B) 1
C) 2
D) 3
E) 4
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 8 :
El número de hijos por familia en una determinada ciudad es una variable aleatoria H, cuya función de probabilidad es
f(x)=P[H=x]=Kx/5
x = 1; 2; 3; 4; 5
¿Cuál es la probabilidad de que una familia tenga 3 hijos dado que tiene al menos dos hijos?
A) 0,200
B) 0,333
C) 0,214
D) 0,267
E) 0,357
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 9 :
Se elige aleatoriamente un número entero de cinco cifras. Calcule la probabilidad que dicho número sea par y la suma de sus cifras sea 42.
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 10 :
RESOLUCIÓN :
Rpta. : "D"
