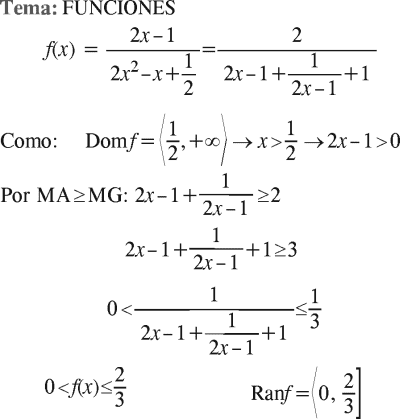ÁLGEBRA UNI RESUELTA DE INGRESO UNIVERSIDAD INGENIERÍA
PREGUNTA 1 :
Sean las ecuaciones
y=x2–3x+4
y=mx+3
Determine los valores reales de m para que nunca se intersequen.
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 2 :
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 3 :
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 4 :
Halle el polinomio p(x) de coeficientes racionales de menor grado con raíces 1 y 1+√2, y que además cumpla p(0)=1.
Dé como respuesta la suma de los coeficientes del polinomio.
A) –2
B) –1
C) 0
D) 1
E) 3
RESOLUCIÓN :
Del dato se tiene que 1 es una raíz.
Entonces
P(1)=0
Por propiedad
P(1) = suma de coeficientes
→ P(1)=0= suma de coeficientes
Rpta. : "C"
PREGUNTA 5 :
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 6 :
Calcule:
Dar como respuesta la primera cifra decimal.
A) 0
B) 1
C) 2
D) 3
E) 4
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 7 :
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 8 :
Al efectuar la división
el término independiente del cociente que resulta es
A) – 2n
B) – n
C) 0
D) n
E) 2n
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 9 :
Determine los puntos de intersección de la gráfica de la función definida por
f(x)=│x–2│+x2 con la recta 3x–2y=–11
A) ( – 1; 2), (3; 9)
B) (1; – 4), (3; 10)
C) (–1; 4), (3; 10)
D) ( – 1; 1), (4; 9)
E) (1; – 4), (3; 12)
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 10 :
RESOLUCIÓN :
Rpta. : "A"
