TRIÁNGULOS PROBLEMAS RESUELTOS PDF PRIMARIA SECUNDARIA Y PRE UNIVERSIDAD
En este capítulo aprenderemos:
• A definir y graficar un triángulo.
• A conocer la clasificación de los triángulos.
• A reconocer los elementos de un triángulo.
• A identificar y aplicar las propiedades fundamentales en el triángulo.
• A reconocer la diferencia entre ángulos internos y externos del triángulo.
Un triángulo es aquella figura geométrica formada por la unión de tres puntos no colineales mediante segmentos de recta.
SUMA DE ÁNGULOS INTERNOS:
La suma de medidas de los ángulos internos en todo triángulo es 180º.
MEDIDA DEL ÁNGULO EXTERIOR:
En todo triángulo, la medida de un ángulo exterior es igual a la suma de las medidas de los dos ángulos interiores no adyacentes a él.
- CLIC AQUÍ Ver TRIÁNGULOS NIVEL BÁSICO EJERCICIOS RESUELTOS
- Ver EXISTENCIA DE UN TRIÁNGULO
- Ver LÍNEAS NOTABLES
- Ver TRIÁNGULOS NOTABLES
- Ver CONGRUENCIA DE TRIÁNGULOS
- Ver PROPIEDADES DE LA CONGRUENCIA
GUIA DE EJERCICIOS
PREGUNTA 1 :
Indicar si es verdadero (V) o falso (F) según corresponda en los siguientes enunciados.
• El triángulo es la figura geométrica que resulta de la unión de tres puntos consecutivos ...( )
• En un vértice, un ángulo interior y un ángulo exterior suman 180º ...( )
PREGUNTA 2 :
Completa los enunciados.
• El triángulo que tiene sus tres lados de igual medida se llama ...
• El triángulo que presenta un ángulo obtuso se llama ...
TEOREMAS FUNDAMENTALES
► En todo triángulo se cumple que la suma de las medidas de sus ángulos internos es igual a 180°.
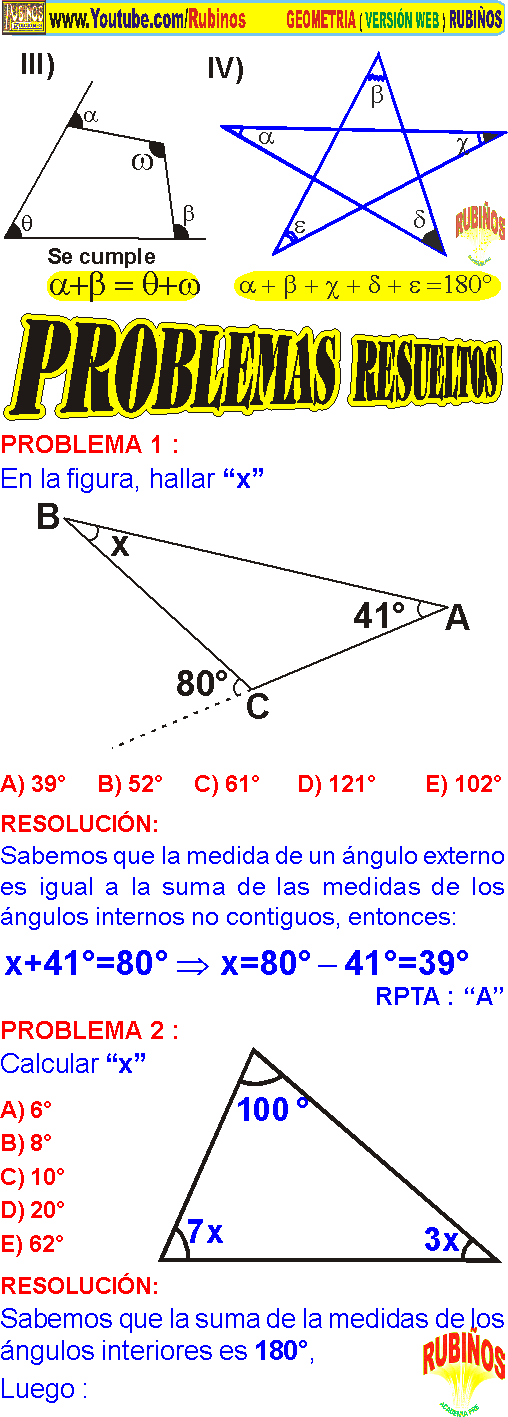
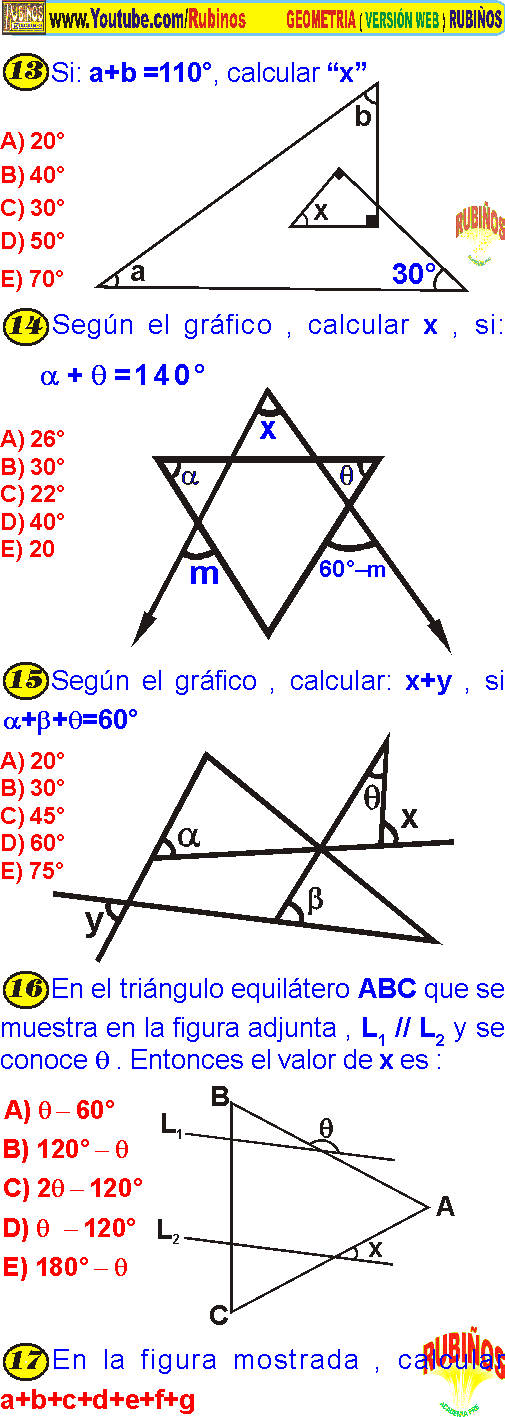
► En todo triángulo, la medida de un ángulo externo es igual a la suma de las medidas de los ángulos internos no contiguos.
► La suma de las medidas de los ángulos externos de un triángulo, uno en cada vértice, siempre es igual a 360°.
CLASIFICACIÓN DE TRIÁNGULOS
A) SEGÚN LA MEDIDA DE SUS ÁNGULOS
I) TRIANGULO Rectángulo :
Es aquel que tiene un ángulo recto y dos ángulos agudos.
Los lados que forman al ángulo recto se llaman catetos y el que se le opone recibe el nombre de hipotenusa.
TEOREMA DE PITÁGORAS
En todo triángulo rectángulo , la suma de los cuadrados de las medidas de los catetos es igual al cuadrado de la medida de la hipotenusa.
II) TRIANGULO Oblicuángulo :
Es aquel que no tiene ángulo recto, puede ser:
a) TRIANGULO Acutángulo :
Es el que tiene 3 ángulos agudos.
b) TRIANGULO Obtusángulo :
Es el que tiene un ángulo obtuso y dos ángulos agudos.
En todo triángulo obtusángulo el lado opuesto al ángulo obtuso es el lado mayor.
B) Según la congruencia de sus lados :
I)TRIANGULO Escaleno :
Es aquel que tiene sus lados diferentes , además sus ángulos también son diferentes.
II)TRIANGULO Isóceles :
Es aquel que tiene dos lados iguales, en consecuencia los ángulos opuestos a dichos lados también son iguales.
En todo triángulo isósceles , al lado desigual se le llama base y al ángulo que se opone a ella se le conoce como ángulo en el vértice o ángulo desigual.
Los dos ángulos de la base son iguales.
III)TRIANGULO Equilátero :
Es aquel que tiene sus tres lados congruentes, tiene también sus tres ángulos congruentes.