SOLUCIONARIO SEMANA 6 2024 PRE SAN MARCOS PDF INGRESO UNIVERSIDAD CEPUSM 2025-1 2023-2 2022

Sexta semana cepre san marcos desarrollada , boletín de ejercicios de clase y preguntas propuestas claves centro preuniversitario–cepusm.
PREGUNTA 1 : 
En la siguiente figura, escribir los números 1, 2, 3, 4, 5, 6, 7 y 8, en ocho de los espacios de esta superficie circular. Si dos números consecutivos no pueden estar compartiendo un lado ni un vértice común, ¿cuál es la suma del mínimo y el máximo valor de los números escritos en los casilleros sombreados? 
A) 36 
B) 37 
C) 38 
D) 39 
E) 40 
Rpta. : "A"
PREGUNTA 2 : 
Un cuadrado mágico multiplicativo es tal que el producto de los números de cada fila, columna y diagonal sea el mismo. Si las casillas del cuadrado del diagrama se llenan con enteros positivos de modo que se forma un cuadrado mágico multiplicativo, ¿cuál es el valor de x? 
A) 1 
B) 2 
C) 3 
D) 4 
E) 5 
Rpta. : "B"
PREGUNTA 3 : 
Complete la siguiente cuadrícula numérica de forma que, en cada fila, en cada columna y en cada rectángulo marcado aparezcan los seis primeros números naturales. ¿Cuál es la suma mínima de los números que serán escritos en los casilleros sombreados? 
A) 6 
B) 9 
C) 8 
D) 7 
E) 5 
Rpta. : "C"
PREGUNTA 4 : 
Los números impares desde 1 hasta 2023 se escriben en la tabla de cinco filas que se muestra parcialmente en la figura, siguiendo el orden de la flecha. ¿En qué ubicación estará el número 2023? 
A) N 201 
B) O 201 
C) P 200 
D) Q 200 
E) N 203 
Rpta. : "E"
PREGUNTA 5 : 
Tony desea formar un cuadrado mágico aditivo, para esto escribirá los números positivos: 4, 6, 8,…,34 uno por casilla, de los cuales algunos ya fueron escritos correctamente por Esteban, como se muestra en la figura. ¿Cuál debe ser el valor de X+Y+Z para que Tony logre su objetivo? 
A) 42 
B) 45 
C) 64 
D) 32 
E) 76 
Rpta. : "A"
PREGUNTA 6 : 
Geiner escribe los números 1; 2; 3; 4; 5 ;….; 24 y 25. En la siguiente cuadrícula de 5×5, de tal manera que logra obtener dos cuadrados mágicos uno de 3×3 y otro de 5×5, tal como indica la siguiente figura. Hallar el valor de (a+b+c+d+e+f – 2). 
A) 78 
B) 52 
C) 80 
D) 74 
E) 82 
Rpta. : "A"
PREGUNTA 7 : 
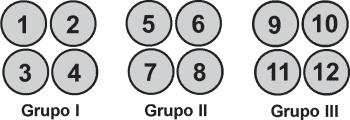
Erika tiene 12 bolos numerados del 1 al 12 los cuales, inicialmente, los agrupó en tres grupos como se muestra en la figura. Manteniendo la misma cantidad de bolos en cada grupo, ¿por lo menos cuántos bolos debe cambiar de posición, sin rotarlas, para que la suma de los números en cada grupo sea la misma? 
A) 5 
B) 4 
C) 3 
D) 6 
E) 2 
Rpta. : "B"
PREGUNTA 8 : 
Escribir los números 22, 23, 24,…, 213 en cada cuadradito, de modo que el producto de los números ubicados en cada lado del cuadrado sea la misma cantidad y la mínima posible. Dé como respuesta la suma de los números ubicados en los vértices del cuadrado. 
A) 60 
B) 120 
C) 30 
D) 240 
E) 480 
Rpta. : "A"
PREGUNTA 1 : 
María que es empleada en una empresa de transportes, trabaja 5 días seguidos y descansa el sexto día. Si ella empieza su trabajo un día viernes, ¿cuántos días tiene que transcurrir como mínimo para que le toque descansar un día jueves? 
A) 41 
B) 42 
C) 35 
D) 49 
E) 43 
Rpta. : "A"
PREGUNTA 2 : 
En un colegio se observa que la cantidad total de alumnos es el mayor número de 3 cifras tal que es múltiplo de 6. Además si se le agrega uno a esta cantidad se convierte en un múltiplo de 7 y si se le agrega uno más se convierte en un múltiplo de 8. Halle la suma de cifras de la cantidad de alumnos que hay en dicho colegio. 
A) 10 
B) 12 
C) 20 
D) 18 
E) 15 
Rpta. : "D"
PREGUNTA 3 : 
Justino le pregunta a su compadre Manuel por la edad de su único hijo Pablo y este le responde: «La edad de mi hijo coincide con la cantidad de divisores positivos múltiplos de seis, pero no de cinco, de un numeral de seis cifras». Si este numeral empieza con tres cifras iguales que son múltiplos de dos y de tres a la vez, y termina en tres ceros; ¿cuántos años tiene Pablo? 
A) 16 
B) 18 
C) 10 
D) 12 
E) 26 
Rpta. : "A"
PREGUNTA 4 : 
Los integrantes de una familia compran un intercomunicador, repartiéndose el pago en partes iguales. Si el número de soles lo que tienen que pagar cada uno de ellos es igual al número de integrantes mas 20 y el precio del intercomunicador no exceden a S/. 300, halle el mayor número de integrantes de dicha familia. 
A) 13 
B) 12 
C) 20 
D) 10
E) 10
Rpta. : "E"
PREGUNTA 5 : 
Para la celebración de las fiestas de fin de año, en una empresa se compró cierta cantidad de regalos para distribuirlos equitativamente entre sus 20 trabajadores. Esta cantidad está representada por el menor número que tiene 3 divisores primos y 14 divisores compuestos. Si cada regalo costó 20 soles, ¿cuánto se gastó en dicha compra? 
A) 3600 
B) 3450 
C) 3260 
D) 3860 
E) 4000 
Rpta. : "A"
PREGUNTA 6 : 
Abel solamente tiene monedas de S/. 0,50. Si al cuadrado del número de soles que tiene, se le disminuye el doble del mismo, le quedaría menos de S/. 360. ¿Cuánto dinero tiene Abel como máximo? 
A) S/. 18,50 
B) S/. 12,50 
C) S/. 39 
D) S/. 20 
E) S/. 19,50 
Rpta. : "E"
PREGUNTA 7 : 
Las hermanas Sonia y Belén aportaron cierta cantidad de dinero para comprar un electrodoméstico. Si el número de soles que aportó Sonia tiene 15 divisores positivos que suman 847 y Belén aportó el doble de lo que aportó Sonia, ¿cuánto costó el electrodoméstico? 
A) 972 
B) 942 
C) 846 
D) 828 
E) 906 
Rpta. : "D"
PREGUNTA 8 : 
¿Cuántos divisores positivos que no son múltiplos de 132 tiene el número 35640? 
A) 56 
B) 64 
C) 72 
D) 84 
E) 36
Rpta. : "B"
PREGUNTA 9 : 
Manuel y Nino tienen la mayor cantidad posible de soles representados por dos números diferentes, ambos de dos cifras y con solo tres factores primos en su descomposición canónica. Si entre los dos desean comprar un regalo cuyo costo en soles coincide con la suma de los divisores positivos del número de soles que tienen juntos, ¿cuánto dinero les falta para comprar dicho regalo? 
A) 156 
B) 168 
C) 186 
D) 148 
E) 176 
Rpta. : "C"
PREGUNTA 10 : 
Determine la suma de cifras de la suma de los divisores positivos de 952875 que son coprimos con 2695. 
A) 8 
B) 7 
C) 6 
D) 4 
E) 3
Rpta. : "D"
PREGUNTA 11 : 
Un profesor de aritmética solicita a sus alumnos que utilicen dos dígitos significativos distintos 𝒂 y 𝒃, donde 𝒂>𝒃 y construyan números de la forma 𝑵=𝒂³−𝒃³ . De acuerdo a lo anterior, indique la alternativa correcta. 
A) 𝑁 siempre es un número compuesto. 
B) Si 𝑎 y 𝑏 son primos, entonces 𝑁 siempre es un número primo. 
C) Por lo menos hay un valor de 𝑁 que es número primo. 
D) La suma de las cifras del menor valor de 𝑁 es 2. 
E) 𝑁 puede tomar valores negativos. 
Rpta. : "C"
PREGUNTA 12 : 
De los 1200 primeros números enteros positivos; indicar la cantidad de números PESI con 1800. 
A) 540 
B) 560 
C) 360 
D) 320 
E) 300 
Rpta. : "D"
PREGUNTA 13 : 
Los divisores primos de un número N son 5 y 7; el número de divisores positivos de su cubo es 589. Hallar la cantidad de divisores positivos compuestos de N. 
A) 120
B) 126 
C) 78 
D) 81 
E) 157 
Rpta. : "E"
PREGUNTA 14 : 
En un salón de clase, los alumnos se dividen en dos grupos. En un grupo, hay 5 alumnos más que en el otro. Si se trasladara 7 alumnos del grupo donde hay más alumnos al otro, entonces el producto de ambas cantidades sería mayor que 286. ¿Cuántos alumnos hay como mínimo en total? 
A) 15 
B) 35 
C) 32 
D) 16 
E) 37 
Rpta. : "E"
PREGUNTA 15 : 
El producto de dos números impares positivos consecutivos no es menor que 195. Halle el menor valor que suman ambos números. 
A) 15 
B) 18 
C) 26 
D) 24
E) 28 
Rpta. : "E"
PREGUNTA 16 : 
La cantidad de alumnos que asistieron a un seminario en el auditorio de un colegio es un número que tiene 8 divisores positivos de los cuales dos son primos. Si la suma de todos los divisores positivos es 320, determine la suma de las cifras de dicha cantidad. 
A) 15 
B) 18 
C) 13 
D) 14 
E) 20
Rpta. : "B"
PREGUNTA 17 : 
Andrés percibe un sueldo de S/ 1800 mensuales. Si desea gastarlo todo de todas las formas posibles, una misma cantidad entera de soles en cada caso, ¿cuánto será la suma de todas esas cantidades enteras? 
A) 5384 
B) 6072 
C) 6288 
D) 7230 
E) 6045 
Rpta. : "E"
PREGUNTA 18 : 
Lucía tiene en su librería una cantidad de lápices que es un número par. Si dicha cantidad es la menor posible y tiene 18 maneras diferentes de empaquetar todos los lápices en bolsas que tengan la misma cantidad, ¿cuántos lápices tiene Lucía? 
A) 344 
B) 338 
C) 242 
D) 252 
E) 288 
Rpta. : "E"
PREGUNTA 19 : 
En una bodega se encuentran almacenados 15 toneles de vino, cada uno con una capacidad de 144 litros. Se desea vender el vino de cada tonel en envases idénticos y llenos con una capacidad entera de litros, sin dejar vino en ninguno de los toneles. Además, se busca utilizar una medida de envase diferente para cada tonel. ¿Cuántos envases necesitará Manuel para realizar esta tarea? 
A) 403 
B) 544 
C) 305 
D) 234 
E) 425 
Rpta. : "A"
PREGUNTA 20 : 
De norte a sur y sobre el lado derecho de una avenida de 2464 metros de largo, se desea colocar cámaras de videovigilancia, de modo que la distancia de una cámara a otra sea la misma y un número entero de metros. Si necesariamente debe haber más de dos cámaras, considerando una al inicio y una al final de la avenida, ¿de cuántas maneras distintas se pueden colocar las cámaras? 
A) 24 
B) 35 
C) 18 
D) 14 
E) 20 
Rpta. : "A"
PREGUNTA 1 : 
Una de las máquinas envasadoras llena 120 envases de 1 litro de leche cada hora. La sección de almacenaje, por cuestión de costos, necesita empaquetarlos en cajas que contengan un número de envases impar. Halle el número de formas que puede hacerlo, para almacenar los envases producidos en una hora. 
A) 4 
B) 5 
C) 6 
D) 3 
PREGUNTA 2 : 
En una tienda se venden jarras de chicha morada de 12 litros cada una. El comerciante distribuye el contenido de cada jarra en envases que contiene igual cantidad entera de litros. ¿Cuántos envases habrá empleado? 
A) 28 
B) 24 
C) 36 
D) 16 
PREGUNTA 3 : 
A lo largo de cincuenta kilómetros de una carretera se desea colocar señales de tránsito, de tal manera que la distancia entre señal y señal sea la misma y un número entero de metros. Si al inicio y al final de este tramo debe colocarse una señal, ¿de cuántas maneras diferentes se pueden colocar las señales en dicha carretera? 
A) 18 
B) 30 
C) 24 
D) 12 
PREGUNTA 4 : 
Si el producto de los divisores de un número N es 331 776, determine la suma de los divisores del número N. 
A) 60 
B) 36 
C) 64 
D) 72 
PREGUNTA 5 : 
Luis profesor del CEPRE le dice a sus estudiantes: “tengo dos nietos cuyas edades son números primos que suman 36 y el producto de las edades más uno, tiene 15 divisores positivos. Determine la suma de cifras de la mayor edad. 
A) 10 
B) 11 
C) 12 
D) 7 
PREGUNTA 6 : 
Cuando un número entero se divide entre 9 su cantidad de divisores disminuye en 8. Si se multiplica el mismo número por 27, ¿cómo varía el número de divisores? 
A) 10 
B) 16 
C) 15 
D) 12 
PREGUNTA 7 : 
Un número entero positivo de tres cifras admite ocho divisores positivos, de los cuales tres son primos; además la suma de sus divisores positivos, que son múltiplos de 13, es 624. Determine el producto de las cifras del mayor número posible, que cumpla las condiciones anteriores. 
A) 100 
B) 120 
C) 80 
D) 90 
PREGUNTA 8 : 
¿Cuántas ventanas de forma de triángulo rectángulo, donde la base es un cateto, existen tal que tengan un área de 12 376 cm², si la medida de la base y respectiva altura son números enteros en centímetros? 
A) 30 
B) 40 
C) 36 
D) 32

Ejercicios resueltos de examen de admisión a la Universidad