FUNCIÓN TANGENTE EJERCICIOS RESUELTOS DE DOMINIO RANGO PERIODO Y GRÁFICA DE LA RAZÓN TRIGONOMÉTRICA PDF
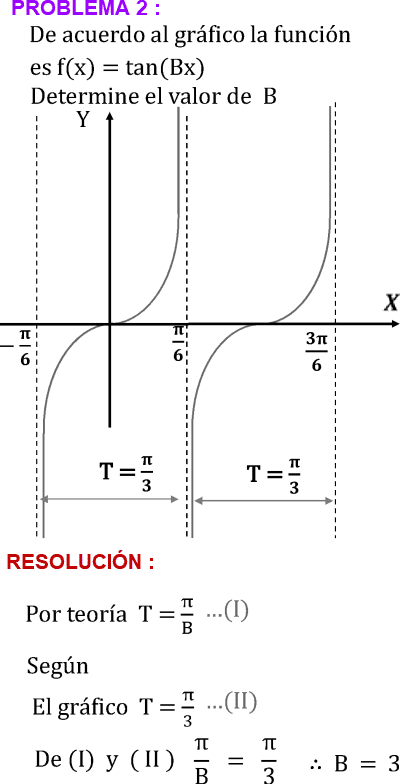
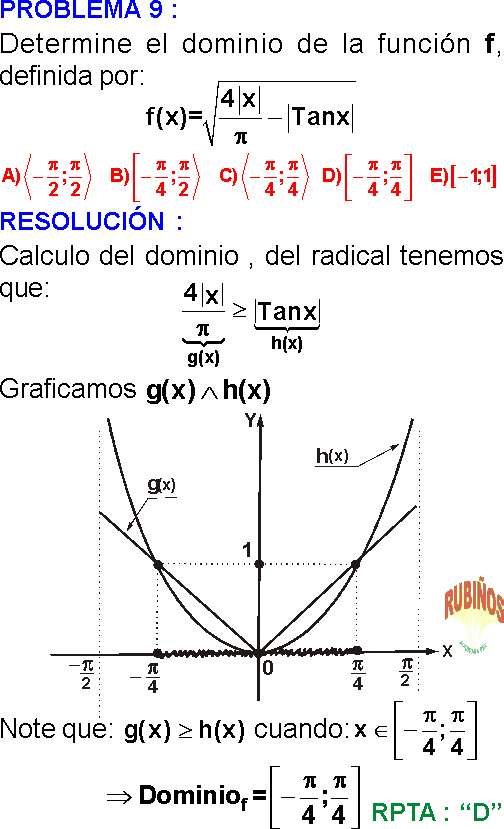
GRÁFICA DE LA FUNCIÓN TRIGONOMÉTRICA TANGENTE
☛ Para determinar los puntos de la función tangente se da valores a x (números reales)
☛ La función no está acotada inferior ni superiormente, esto significa que no tiene máximo ni mínimo valor.
☛ Curva : tangentoide
Una parte de la gráfica de la función coseno se repite por tramos de longitud 𝛑.
Esto quiere decir que la gráfica de la función tangente es el periodo 𝛑 ; por lo tanto, todo análisis y cálculo del dominio y rango se hace en el siguiente gráfico.
☛ Función impar en **
☛ Función creciente en **
☛ Continua en **
PROBLEMAS RESUELTOS
PROBLEMAS PROPUESTOS
PREGUNTA 1 :
La trayectoria de un globo se modela mediante la gráfica de una función tangente, donde x y f(x) representan los desplazamientos horizontal y vertical del globo en metros con dominio de f igual a [0;6[ Si Lenin tiene una altura de un metro y observa al globo desde el punto A, determine el ángulo de elevación aproximado con el que Lenin observa el globo cuando este pasa por el punto B.
A) 30°
B) 45°
C) 53°
D) 37°
Rpta. : "C"
PREGUNTA 2 :
En la figura, se representa la trayectoria de un globo que se mueve desde un punto O en el suelo y va elevándose hasta llegar a 2 000 m de altura donde explota. Si dicha trayectoria está representada por la gráfica de la función real f, definida por f(x)=2tan(𝛑x/4), determine el ángulo de elevación con el cual se observa al globo explotar desde el punto O.
A) 37°
B) 63,5°
C) 26,5°
D) 60°
Rpta. : "B"
PREGUNTA 3 :
Una nave espacial, despega al espacio desde una plataforma que se encuentra a 1500 metros sobre el nivel mar; durante su desplazamiento, la altura es modelada por la función real f, definida como f(t)=98,5tan(𝛑t/10) en kilómetros, donde 0 ≤ t ≤ 4 , es el número de horas transcurridas desde que la nave despega de la plataforma. Si el espacio exterior comienza a los 100 km de altura sobre el nivel del mar, ¿cuántas horas le toma a esta nave llegar al espacio?
A) 1hora
B) 1,5 horas
C) 2,5 horas
D) 3 horas
Rpta. : "C"
PREGUNTA 4 :
La asistencia del público en un centro comercial desde las 11:00 a.m. hasta 11:00 p.m. esta modelada por
f(x)=4sec²(𝛑x/36)+20tan(𝛑x/36)+21
en cientos de personas, donde x∈[0,12] son las horas de atención transcurridas desde las 11 de la mañana. ¿Cuántas personas, como mínimo, asistieron desde las 11:00 a.m. hasta 11:00 p.m. a dicho centro comercial?
A) 2 500 personas
B) 2 550 personas
C) 2 450 personas
D) 2 525 personas
Rpta. : "A"
PREGUNTA 5 :
La figura muestra 2 rutas de tren representadas por las gráficas de las funciones reales f y g cuyas reglas de correspondencias son
f(x)=sen(𝛑x/2), con x∈[0;2] y g(x)=0,5tan(𝛑x/4) donde x∈[0;19/10] . Si el ingeniero Edu parte desde el almacén ubicado en el punto O en dirección al punto donde se intersecan las rutas para colocar un semáforo, ¿a cuántos kilómetros aproximadamente al Este del punto O, se colocará el semáforo?
A) 1,23 km
B) 1,45 km
C)1, 56 km
D) 1,33 km
Rpta. : "D"