FUNCIÓN SECANTE EJERCICIOS RESUELTOS DE DOMINIO RANGO PERIODO Y GRÁFICA DE LA RAZÓN TRIGONOMÉTRICA PDF
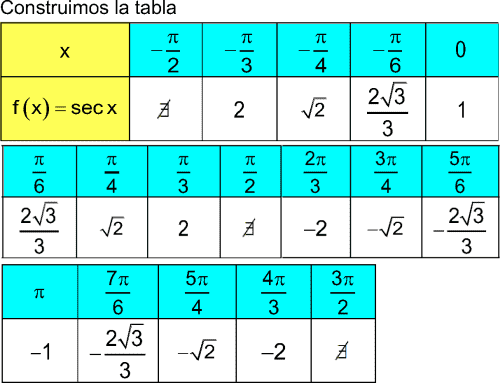
GRÁFICA DE LA FUNCIÓN TRIGONOMÉTRICA SECANTE
La función secante es una función periódica y su periodo es T=2𝛑 , es decir, sec(x+2𝛑)=secx , para todo x en su dominio.
☛ Curva : Secantoide
PREGUNTA 1 :
La figura muestra la vista lateral de un teleférico que une el punto A con el punto B y cuyo trayecto lo realiza en 30 minutos. La función real f, definida por
.png){kind=small}
modela a qué altura se encuentra el punto P con respecto al suelo, donde x es el número de minutos transcurridos. Si el teleférico parte a las 8:00 a.m. del punto A, ¿a qué altura se encontrará el punto P a las 8:15 a.m.?
.png)
.png)
RESOLUCIÓN :
.png)
Rpta. : "A"
PREGUNTA 2 :
El rendimiento del combustible en un automóvil cuando se desplaza a velocidades constantes entre 40 km/h y 120 km/h está modelado por la función real r definida por
.png)
, − 150 < C < 0 , expresada en kilómetros por litros de combustible, donde v es el número de kilómetros por hora a la que se desplaza el automóvil. Si cuando el automóvil se desplaza a 40 km h el rendimiento del combustible es 9,64 km , ¿a qué velocidad debe desplazarse dicho automóvil para obtener un l máximo rendimiento del combustible?
A) 120 km h
B) 100 km h
C) 60 km h
D) 80 km h
RESOLUCIÓN :
.png)
Rpta. : "B"
