TEOREMA DE THALES MENELAO CEVA TEOREMAS DE LA BISECTRIZ INTERIOR Y EXTERIOR EJERCICIOS RESUELTOS DE PROPORCIONALIDAD GEOMÉTRICA PDF
OBJETIVOS :
☛ Conocer las principales figuras cuyos segmentos asociados a ellas guardan propiedad de proporcionalidad.
☛ Establecer la definición de razón de segmentos y segmentos proporcionales.
☛ Usar los conceptos y propiedades básicas para solucionar problemas y hacer demostraciones de teoremas
☛ Utilizar adecuadamente dichos conceptos en el desarrollo de ejercicios que involucren la comparación de 2 o más segmentos.
PREGUNTA 1 :
En un triángulo ABC, las cevianas interiores AP y BQ se cortan en el punto R. Si BC=24 cm; QC=3AQ y BR=2RQ, halle la longitud BP.
A) 6 cm
B) 12 cm
C) 9 cm
D) 8 cm
E) 4 cm
RESOLUCIÓN :
Rpta. : "D"
TEOREMA DE THALES DE MILETO
Tres o más rectas paralelas determinan en dos rectas transversales a ellas, segmentos cuyas longitudes son proporcionales.
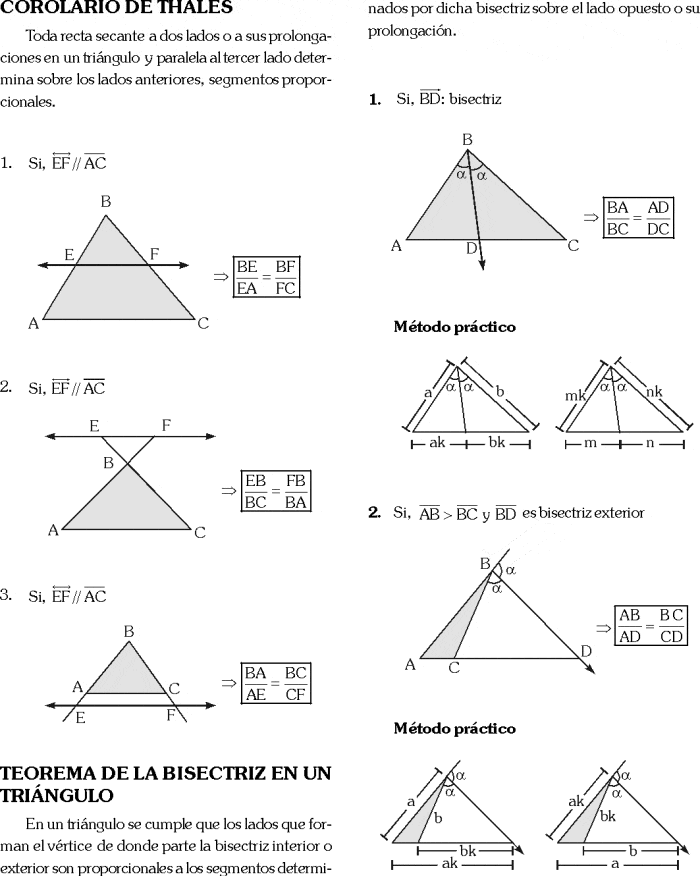
COROLARIO DE THALES
Toda recta paralela, a uno de los lados de un triángulo, divide a los otros dos lados en segmentos cuyas longitudes son proporcionales.
TEOREMA DE LA BISECTRIZ INTERIOR
En todo triángulo una bisectriz interior, divide al lado al cual es relativo en segmentos cuyas longitudes son proporcionales a las longitudes de los lados adyacentes a dicha bisectriz.
TEOREMA DE LA BISECTRIZ EXTERIOR
En todo triángulo una bisectriz exterior (tal que los lados adyacentes a dicha bisectriz son de longitudes diferentes) divide a la prolongación del lado al cual es relativa en segmentos cuyas longitudes son proporcionales a los lados adyacentes a dicha bisectriz.
TEOREMA DE LA CEVA
En todo triángulo, tres cevianas interiores concurrentes dividen a cada lado en dos segmentos, cumpliéndose que el producto de las longitudes de tres de ellos, sin extremo común es igual al producto de las longitudes de los otros tres.
TEOREMA DEL INCENTRO Y BARICENTRO
Si en un triángulo se cumple que el segmento que une al baricentro con el incentro es paralelo a un lado entonces dicho lado será igual a la semisuma de los otros dos lados.
Si los lados de un triángulo forman una progresión aritmética, entonces en dicho triángulo, el segmento que une el incentro con el baricentro será paralelo al lado cuyo valor es medio respecto a los otros.