PROPORCIONALIDAD DE SEGMENTOS EJERCICIOS RESUELTOS PDF

OBJETIVOS DE APRENDIZAJE

• Aplicar correctamente el teorema de thales y sus corolarios en la resolución de problemas.

• Comprender el teorema de la bisectriz a partir del teorema de thales.

• Resolver problemas tipo examen de admisión ya que es un tema frecuente.

RAZÓN DE SEGMENTOS :

Es el cociente de las longitudes de dichos segmentos, expresadas en la misma unidad de medida, dicha razón no tiene unidades.

SEGMENTOS PROPORCIONALES

Dos segmentos son proporcionales a otros dos segmentos, cuando la razón entre sus longitudes es la misma.

TEOREMA DE THALES

Tres o mas rectas paralelas determinan sobre dos rectas secantes segmentos proporcionales

COROLARIO DEL TEOREMA DE THALES

Una recta secante a un triángulo y paralela a un lado, determina en los otros dos lados o sus prolongaciones segmentos proporcionales.

TEOREMA DE LA BISECTRIZ

En todo triángulo los lados adyacentes de una bisectriz son proporcionales a las segmentos determinados en su lado relativo.

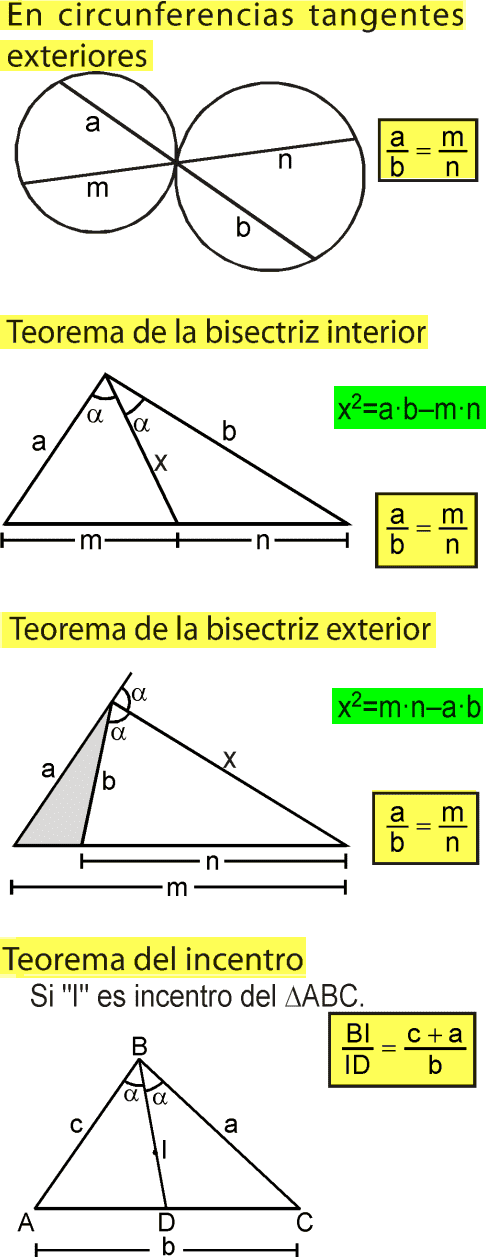
TEOREMA DE LA BISECTRIZ INTERIOR

En todo triángulo , una bisectriz interior determina en el lado al cual es relativa segmentos proporcionales a los adyacentes a dicha bisectriz.

TEOREMA DE LA BISECTRIZ EXTERIOR

En un triángulo , una bisectriz exterior cuyos lados adyacentes son de diferente longitud ; determina en el lado al cual es relativa segmentos proporcionales a lados adyacentes a dicha bisectriz.

TEOREMA DEL INCENTRO

En todo triángulo el incentro divide a una bisectriz interior en dos segmentos que son proporcionales a la suma de las longitudes de los lados adyacentes a la bisectriz y a la longitud del lado al cual es relativa dicha bisectriz .

TEOREMA DE MENELAO

Toda recta secante a un triángulo que interseca a dos lados y al tercero en la prolongación , determina en dichos lados segmentos , de modo que el producto de las longitudes de tres de ellos sin extremo común es igual al producto de las longitudes de los otros tres.

TEOREMA DE LA CEVA

En todo triángulo tres cevianas concurrentes, determinan en los lados, segmentos, de modo que el producto de las longitudes de tres de ellos sin extremo común es igual al producto de las longitudes de los otros tres.

DIVISIÓN ARMÓNICA DE UN SEGMENTO

Dos puntos dividen armónicamente a un segmento, si lo dividen internamente y externamente en la misma razón.

TEOREMA

En un triángulo , las bisectrices de un ángulo interior y de su correspondiente (o adyacente) ángulo exterior; dividen armónicamente al lado opuesto a dicho ángulo.

PROBLEMAS RESUELTOS

PREGUNTA 1 :

En la figura las medidas están dadas en centímetros.