PROPIEDADES EN LA CIRCUNFERENCIA EJERCICIOS RESUELTOS DE GEOMETRÍA PREUNIVERSITARIA PDF
Desde que el ser humano se topo con la circunferencia, le saco mucho provecho, hoy podemos apreciarla en casi todos los dispositivos electrónicos, así como también empleada para la recreación.
El contorno de una tapa nos da la idea de circunferencia, dicho contorno se puede medir, por ejemplo con una cinta métrica.
*
POSICIONES RELATIVAS DE DOS CIRCUNFERENCIAS
Dos circunferencias de centro O1 y O2 en un mismo plano y de radios R y r respectivamente, pueden tener las siguientes proposiciones.
1 Circunferencias Exteriores:
Si la distancia entre los centros es mayor que la suma de sus radios. d > R + r
2. Circunferencias tangentes exteriores
Es la distancia entre los centros es igual a la suma de los radios. d = R + r T :
Punto de Tangencia
• El segmento que une los centros pasa por el punto de tangencia.
• La recta tangente común interior a ambas circunferencias es perpendicular al segmento que une sus centros.
3. Circunferencias Secantes
Su la distancia entre los centros es menor que la suma de los radios y mayor que su diferencia. d = O1 O2 R – r < d < R + r Existencia del triángulo
• Tiene dos puntos comunes (A y B)
• La cuerda común AB es perpendicular al segmento que une los centros
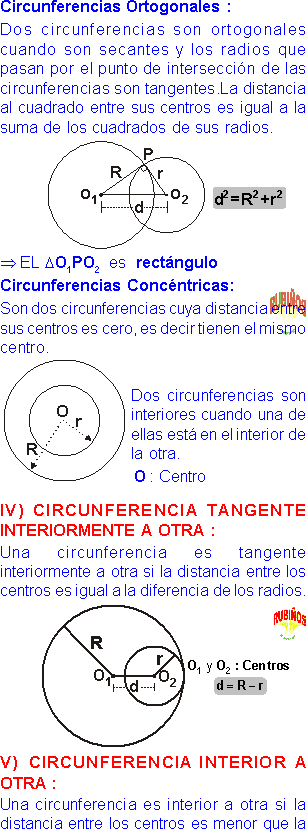
4. Circunferencias Ortogonales
Si el cuadrado de la distancia entre los centros es igual a la suma de los cuadrados de los radios. d² = R² + r² m01BO2 = 90º L1 : Recta tangente a la circunferencia de centro O2 en el punto B L2 : Recta tangente a la circunferencia de centro O1 en el punto B
5. Circunferencias tangentes interiores
Si la distancia entre los centros es igual a la diferencia de los radios. L : Tangente común d = R - r T : Punto de Tangencia * La recta que pasa por los centros, también pasa por el punto de tangencia y es perpendicular a la recta tangente común.
6. Circunferencias Interiores
Si la distancia entre los centros es menor que la diferencia de los radios. d + r < R d < R – r • Los puntos de una de ellas (circunferencia de centro O2) son interiores a la otra. (Circunferencia de centro O1)
7. Circunferencias concéntricas
Si la distancia entre los centros es cero, es decir, sus centros coinciden. (Tienen el mismo centro). M : Punto de tangencia OMB : PITÁGORAS = R² - r² AB = 2







































































.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)

