CIRCUNFERENCIA EJERCICIOS RESUELTOS PDF
OBJETIVOS DE APRENDIZAJE
☛ Relacionar correctamente los teoremas en la circunferencia con los ejercicios
☛ Reconocer los diferentes teoremas a partir de tangentes y cuerdas asociadas a la circunferencia.
☛ Analizar las diferentes posiciones entre dos circunferencias coplanares a partir de la distancia entre sus centros.
☛ Aplicar correctamente los teoremas Poncelet , Pithot , Steiner , ....,etc.
☛ Resolver problemas tipo exámenes de admisión.
Las necesidades y los momentos en que se vive, hace que descubramos o inventemos cosas , es así como nace la rueda la cual se caracteriza por tener la forma de una circunferencia. Dicho objeto fue y es de mucha utilidad y así como él, hay otros objetos que adoptan esa misma forma tales como: los ventiladores, los timones de los carros, etc.
En base a ello podemos notar que la circunferencia es una figura geométrica de mucha importancia.
En la actualidad, la encontramos en todos los campos de la técnica. Concretamente en arquitectura, aparece en rosetones, columnas de sección circular y otros ornamentos, donde desempeña un papel importante.
Nosotros mismos, en los temas que anteceden, hemos hecho uso del compás para el trazado de circunferencias. Sin embargo no es el único instrumento utilizado para tal fin.
CIRCUNFERENCIA
Es aquella figura geométrica formada por infinitos puntos, los cuales equidistan de un punto fijo coplanar a ella.
CIRCUNFERENCIAS EXTERIORES
Son dos circunferencias coplanares cuya distancia entre sus centros es mayor a la suma de sus radios.
CIRCUNFERENCIAS TANGENTES EXTERIORES
Son dos circunferencias coplanares cuya distancia entre sus centros es igual a la suma de radios.
CIRCUNFERENCIAS SECANTES
Son dos circunferencias coplanares cuya distancia entre sus centros es mayor a la diferencia y menor a la suma, de sus respectivos radios.
CIRCUNFERENCIAS TANGENTES INTERIORES
Son dos circunferencias coplanares cuya distancia entre sus centros es igual a la diferencia de radios.
CIRCUNFERENCIAS CONCÉNTRICAS
Son aquellas circunferencias coplanares que tienen el mismo centro
TEOREMA DE PONCELET
En todo triángulo rectángulo que presenta una circunferencia inscrita se cumple que la suma de longitudes de los catetos es igual a la suma de la longitud de la hipotenusa y dos veces su inradio.
TEOREMA DE PITOT
En todo cuadrilátero circunscrito, la suma de las longitudes de sus lados opuestos, son iguales.
GUIA DE EJERCICIOS
PREGUNTA 1 :
En un triángulo rectángulo sus catetos miden 15m y 20m. Hallar su inradio.
A) 3
B) 5
C) 6
D) 8
E) 12
Rpta. : "B"
PREGUNTA 2 :
En un triángulo ABC, de lados: AB = 8, BC = 10 y AC = 12, la circunferencia inscrita determina sobre AC el punto “M”. Calcular “AM”.
A) 3
B) 5
C) 6
D) 8
E) 12
Rpta. : "B"
PREGUNTA 3 :
Se tiene un triángulo rectángulo de semiperímetro 16 cm y de inradio 4 cm. Calcular la longitud de su hipotenusa.
A) 13
B) 15
C) 16
D) 18
E) 12
Rpta. : "E"
PREGUNTA 4 :
En un triángulo rectángulo la hipotenusa mide 14 y el radio de la circunferencia inscrita mide 4. hallar el perímetro del triángulo.
A) 36
B) 12
C) 48
D)18
E) 30
PREGUNTA 5 :
En un triángulo rectángulo de semiperimetro igual a 32 unidades, el radio de la circunferencia inscrita mide 6 unidades. Calcular la longitud de la hipotenusa.
A) 26
B) 24
C) 32
D) 25
E) 30
PREGUNTA 6 :
El perímetro de un cuadrilátero circunscrito a una circunferencia es 20 y el lado menor mide 3. ¿Cuánto mide el lado mayor?
A) 6
B) 7
C) 8
D) 9
E) 10
PREGUNTA 7 :
La mediana de un trapecio rectángulo circunscrito a una circunferencia mide 18 cm y uno de los ángulos, 53°. Calcular el radio de la circunferencia inscrita
A) 2 cm
B) 8 cm
C) 6 cm
D) 3 cm
E) 5 cm
PREGUNTA 8 :
Calcular el semiperímetro de un triángulo rectángulo, sabiendo que el inradio mide 2m y la longitud de la hipotenusa es 13 m.
A) 12 m
B) 13 m
C) 15 m
D) 21 m
E) 28 m
PREGUNTA 9 :
En un triángulo rectángulo sus catetos miden 15m y 20m. Hallar su inradio.
A) 3
B) 5
C) 6
D) 8
E) 12
PREGUNTA 10 :
En un triángulo rectángulo, calcular la longitud de la hipotenusa si los exradios relativos a los catetos miden 2 y 3.
a) 2
b) 3
c) 4
d) 5
e) 6
PROBLEMAS RESUELTOS
PREGUNTA 1 :
El perímetro de un triángulo rectángulo es 48 m y su hipotenusa mide 20 m. Hallar la longitud de su inradio.
A) 4 m
B) 5 m
C) 6 m
D) 2 m
E) 3 m
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 2 :
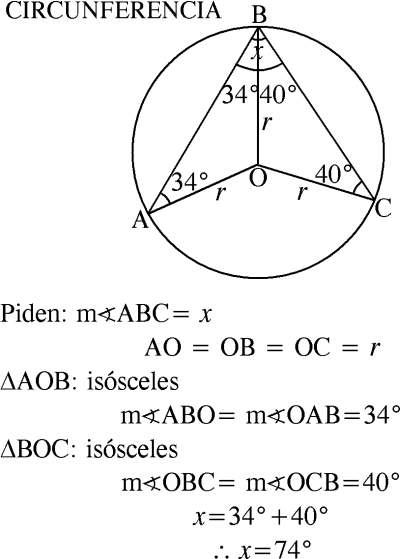
En la clase de Geometría, el profesor indica la importancia de la circunferencia en diferentes aspectos de la vida diaria; para ello utiliza un transportador que, como sabemos, nos sirve para medir ángulos o dibujar circunferencias, tal como se muestra en la figura. Si el punto O es centro de la circunferencia, ¿cuál es la medida del ángulo ∠ABC?
A) 68º
B) 72º
C) 84º
D) 74º
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 3 :
Un cuadrilátero ABCD está circunscrito a una circunferencia, m∠A=90° y T es punto de tangencia en BC; si AD=15 cm, DC=24 cm y CT=18 cm, halle la medida del radio de la circunferencia.
A) 7 cm
B) 6 cm
C) 9 cm
D) 10 cm
E) 8 cm
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 4 :
En la siguiente figura, CD es tangente, CD=2√21cm, AB=diámetro y BC=6cm; hallar la medida del radio de la circunferencia.
A) 1 cm
B) 2 cm
C) 3 cm
D) 4 cm
E) 5 cm
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 5 :
Calcular la longitud del radio de la circunferencia mostrada, si O=centro, AD=OD , ED=4u , CD=8u
A) 2 u
B) 4 u
C) 6 u
D) 8 u
E) 10 u
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 6 :
Se tiene una circunferencia de radio T, si se duplica su radio, la longitud de la circunferencia mayor es x veces la longitud de la circunferencia menor.
Calcule x
A) 3
B) 2,5
C) 1
D) 2
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 7 :
En una circunferencia 𝒞 cuyo radio mide 10cm, se inscribe un cuadrilátero ABCD. Si m∢CAD=45°, AB=BD, ℓ1 es la longitud del arco BC y ℓ2 es la longitud del arco AD, calcule (en cm) 2ℓ1+ ℓ2.
A) 12𝛑
B) 10𝛑
C) 7𝛑
D) 15𝛑
E) 5𝛑
RESOLUCIÓN :
Rpta. : "B"
