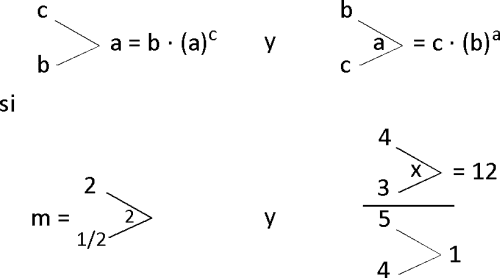OPERADORES MATEMÁTICOS EJERCICIOS RESUELTOS PDF RAZONAMIENTO MATEMÁTICO

OBJETIVOS DEL APRENDIZAJE
☛ Reconocer la importancia de la regla de definición en la resolución de nuevas operaciones matemáticas 
☛ Conocer y utilizar diversos métodos prácticos para la resolución de problemas 
☛ Resolver problemas de operaciones matemáticas con regla de definición implícita 

OPERACIÓN MATEMÁTICA 
Es aquel procedimiento que transforma una o más cantidades en otra cantidad denominada resultado, bajo cierto criterio o ley de formación. 
Toda operación matemática tiene un símbolo que lo caracteriza denominado operador matemático. 

¿QUÉ ES UN OPERADOR MATEMÁTICO? 
Es aquel símbolo que representa a una operación matemática. 
Nos permite reconocer la operación matemática a emplear con su respectiva regla de definición.

OPERACIONES MATEMÁTICAS UNIVERSALES 
Son operaciones matemáticas convencionales cuyas reglas de definición son conocidas y universalmente aceptadas 

OPERACIONES MATEMÁTICAS ARBITRARIAS 
Son operaciones matemáticas no convencionales. 
Requieren de una regla de definición establecida y utilizan operadores matemáticos arbitrarios como se muestra a continuación. 
☛ Operaciones con Regla de definición explícita 
☛ Operaciones con Regla de definición implícita 
☛ Operaciones Definidas mediante tablas
Este capítulo basa su importancia en la gran aplicación que tiene sobre los procesos condicionados y reglamentados, que permite medir la capacidad para captar relaciones u operaciones nuevas, a las que se supone estamos poco acostumbrados. 
Permite también analizar nuevas operaciones matemáticas (definidas a partir de las ya conocidas), su definición y el modo de aplicarlas bajo las condiciones o restricciones en las cuales ha sido definida. Para tal efecto, debemos entender lo que es una operación matemática y lo que es un operador matemático. 

    Imaginemos que tenemos una máquina procesadora de algodón, tal como se muestra en la figura; esta máquina recibe la materia prima que es el algodón y la transforma en un producto terminado, después de un determinado proceso, dependiendo del botón que se haya escogido. 

    Igual ocurre con una operación matemática (representada por la máquina), ya que ella se encarga de obtener resultados, después de un conjunto de procesos que se efectúan sobre determinadas cantidades; estos procesos son diferenciados por el operador que se emplee (representado por los botones).
PROBLEMAS RESUELTOS
PREGUNTA 1 : 
Si ✎a= a(a – 1)
Calcular ✎(✎7)
A) 243 
B) 200 
C) 2100 
D) 1722 
E) 1850 
RESOLUCIÓN :
(✎7)=7×6=42
⇒ ✎(42)=42×41=1722 
Rpta. : "D"
PREGUNTA 2 : 
En ℝ definimos la operación matemática representada por * mediante 
Determine el valor de 1* 3 
A) 1 
B) 2 
C) 3 
D) 4 
E) 5 
RESOLUCIÓN : 
Rpta. : "D"
PREGUNTA 3 : 
Si a² Δ b³=3a+4b
Hallar 64 Δ 64. 
A) 36 
B) 28 
C) 32 
D) 24 
E) 40 
RESOLUCIÓN :
Del dato a² Δ b³=3a+4b
Damos forma a los pedido, para a= 8 y b= 4 
Reemplazamos:
64 Δ 64=8² Δ 4³
⇒ 64 Δ 64 = 3(8) + 4(4) =40
Rpta. : "E"
PREGUNTA 4 : 
Dados el operador definido mediante: 
A) 3 
B) 5/2 
C) 1 
D) 2 
E) 4/3 
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 5 : 
A) 2 
B) 4 
C) 5 
D) 6 
E) 3 
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 6 : 
Dados los operadores: 
a♥b=ab+ba; (a+b) par 
a♥b=ab; (a+b) impar 
Halle el valor de E= (2♥1)♥(1♥3) 
A) 30 
B) 36 
C) 32 
D) 28 
E) 26 
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 7  : 
A) 7/8 
B) 3/2 
C) 3/4 
D) 4/3 
E) 5/6 
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 8 : 
Se define el operador * mediante
A) 0 
B) 1 
C) 2 
D) 3 
E) 4 
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 9 : 
Dados los operadores definidos mediante: 
Halle el valor positivo de m en la ecuación 
A) 5 
B) 8 
C) 1 
D) 2 
E) 10 
RESOLUCIÓN :
Rpta. : "B"

PREGUNTA 10 : 
Dados dos operadores definidos mediante 
A) 20 
B) 0 
C) –20 
D) –42 
E) –36 
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 11 :  
Hallar el valor de "x" en la expresión: 
a) 2 
b) 4 
c) 7 
d) 8 
e) 6 
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 12 : 
Si: 
u → t =2u+ t
u ↑ t =2t +u 
u ← t =4t –1
u ↓ t = 1– 4u 
Determine el valor de x en la ecuación 
(5 ← x)–[(5 → x) + (5 ↑ x) + (5 ↓ x)]=5 
A) 0 
B) 1 
C) 2 
D) 3 
E) 4 
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 13 :
Si definimos el operador *, entre los números reales, por *(a + b) = a + *(b), tal que *(3) = 5, entonces el valor de la expresión *(20) es: 
A) 20 
B) 21 
C) 22 
D) 23 
E) 24 
RESOLUCIÓN :
Utilizamos la regla del operador ∗ : 
∗ (𝑎 + 𝑏) = 𝑎 + ∗ (𝑏)
∗ (3) = 5 
Descomponemos: 20 = 17 + 3
Luego ∗ (20) = ∗ (17 + 3) = 17 +∗ (3) 
= 17 + 5 = 22 
Rpta. : "C"
PREGUNTA 14 : 
 Definidos los operadores matemáticos por 
Determine el valor de xm 
A) 0 
B) 1 
C) 2 
D) 3 
E) 4 
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 15: 
Se define el operador ∗ por : 
Calcule 32 ∗ 4 
A) 16 
B) 8 
C) 4 
D) 32 
E) 64 
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 16 : 
Dados los operadores definidos mediante 
A) 2 
B) 6 
C) 1 
D) 7 
E) 3 
RESOLUCIÓN :
Rpta. : "C"

PREGUNTA 17 : 
Se define a@b = a + b –100. 
Determinar si cada proposición es verdadera (V) o falsa (F). 
I. El elemento neutro en está operación es 100. 
II. El elemento inverso de 100 es 200. 
III. Para todo a, b, c se cumple que 
(a@b)@c =a@(b@c). 
A) VFF 
B) VVF 
C) VFV 
D) VVV 
E) FFV 
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 18 : 
Dado el operador 
A) 16 
B) 2 
C) 8 
D) 32 
E) 4 
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 19 : 
Sea : a █ b ▀f(x) = f(a + b) – f(a – b)
Para f(x) = 4x + 3
Calcular el valor de E=3 █ 1 ▀f(x)
A) 7 
B) 8 
C) 10 
D) 9 
E) 11
RESOLUCIÓN :
E=3 █ 1 ▀f(x)= f(3 + 1) – f(3 – 1)
= f(4) – f(2)=4(4) + 3 – [4(2) + 3 ] 
= 19 – 11 = 8
 Rpta. : "B"
PREGUNTA 20 : 
Calcule (8*20) # (4*17) 
A) 16 
B) 1 2 
C) 10 
D) 3 
E) 8 
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 21: 
Se sabe que
Halla a+b
A) 13 
B) 9 
C) 6 
D) 10 
E) 5 
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 22: 
Sean las siguientes operaciones: 
x * y = (x + y)/2 
xΔy = (y − x)/2
con las siguientes condiciones: 
I. (x*U) + (x*N) + (x*I) = (UΔx) + (NΔx) + (IΔx) 
II. 
U*N=NΔI
UΔI =2*N 
Halle 
E= (UΔN)*I + (U*N)ΔI +UΔ(N*I) +U*(NΔI) 
A) 3 
B) 5 
C) 6 
D) 8 
E) 11 
RESOLUCIÓN :
Rpta. : "A"

Ejercicios resueltos de examen de admisión a la Universidad