OPERADORES MATEMÁTICOS EN TABLAS EJERCICIOS RESUELTOS PDF ELEMENTO NEUTRO INVERSO PROPIEDAD CONMUTATIVA Y ASOCIATIVA

OPERADORES EN TABLAS DE DOBLE ENTRADA

OBJETIVOS

• Reconocer una operación matemática definida mediante una tabla.

• Aplicar de manera correcta las propiedades de clausura y conmutativa.

• Reconocer los distintos tipo de pregunta que pueden venir en este tema

• Aplicar de manera correcta las propiedades del elemento neutro y elemento inverso de las operaciones matemáticas

• Analizar los diferentes casos que se pueden presentar, con tablas o sin ella

OPERACIONES MATEMÁTICAS DEFINIDAS MEDIANTE TABLAS DE DOBLE ENTRADA

Las operaciones matemáticas también pueden definirse a través de una tabla de doble entrada.

OPERACION BINARIA

(TABLAS DE DOBLE ENTRADA)

A una ley de composición interna se le llama Operación Binaria, la cual puede tener una presentación algebraica o una presentación tabular (pitagórica).

PROPIEDADES DE LAS OPERACIONES MATEMÁTICAS

CLAUSURA O CERRADURA

Si al realizar la operación matemática con 2 elementos cualesquiera del conjunto A, el resultado de esa operación es un elemento del conjunto A, entonces diremos que la operación cumple con la propiedad de clausura o cerradura.

OPERACIÓN CONMUTATIVA ( CONMUTATIVIDAD ) :

Si para todo par de elementos del conjunto A, el orden de esos elementos en la operación matemática no altera el resultado de esta, entonces diremos que la operación cumple con la propiedad de conmutatividad o que la operación es conmutativa.

Las propiedades de las operaciones matemáticas también pueden identificarse en operaciones definidas a través de una tabla de doble entrada.

Conmutatividad en tablas de doble entrada :

Para determinar si la operación mostrada a través de una tabla de doble entrada es o no conmutativa , existe un criterio práctico denominado ‘‘Criterio de la diagonal’’

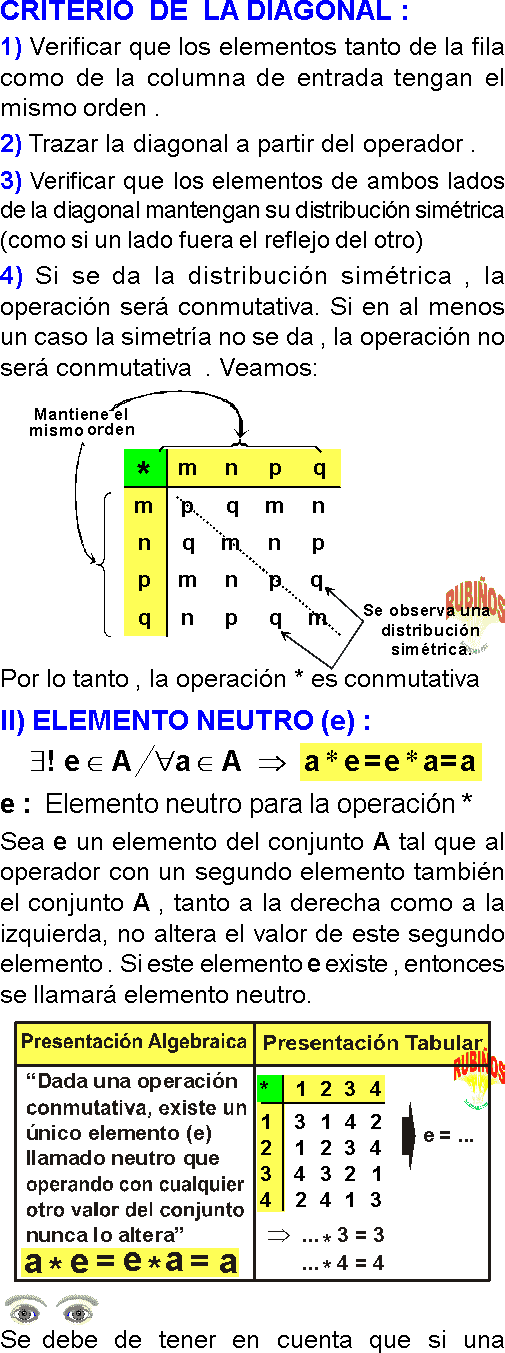
CRITERIO DE LA DIAGONAL :

1) Verificar que los elementos tanto de la fila como de la columna de entrada tengan el mismo orden .

2) Trazar la diagonal a partir del operador .

3) Verificar que los elementos de ambos lados de la diagonal mantengan su distribución simétrica (como si un lado fuera el reflejo del otro)

4) Si se da la distribución simétrica , la operación será conmutativa.

Si en al menos un caso la simetría no se da , la operación no será conmutativa .

ELEMENTO NEUTRO (e) :

Sea e un elemento del conjunto A tal que al operador con un segundo elemento también el conjunto A , tanto a la derecha como a la izquierda, no altera el valor de este segundo elemento . Si este elemento e existe , entonces se llamará elemento neutro.

EN UNA TABLA DE DOBLE ENTRADA :

CRITERIO DE INTERSECCIÓN :

1) Ubicar en el cuerpo de la tabla una columna igual a la columna de entrada y una fila igual a la fila de entrada .

2) La intersección de la columna y la fila mencionadas nos dará el elemento neutro (e)

ELEMENTO INVERSO (a–1) :

Es una operación con elemento neutro , tenemos un elemento a∈A , tal que al ser operado tanto a la derecha como a la izquierda de a da como resultado el elemento neutro de la operación .

Primero identifiquemos el elemento neutro , para luego ubicar a todos iguales a él , después se utilizará un recorrido tipo una ‘‘ELE VOLTEADA’’ partiendo del elemento cuyo inverso se pide (al elemento se ubica en la columna de entrada) , cambiando de dirección en el momento que encontramos a uno igual al elemento neutro , siguiendo hasta la fila de entrada , donde se ubica el inverso pedido .

PROPIEDAD ASOCIATIVA :

Cuando se efectúa con más de dos elementos que pertenecen al conjunto de partida y se agrupa de diferentes maneras , el resultado no cambia.

PROBLEMAS RESUELTOS

EJERCICIO 1 :

Dado el operador definido mediante: