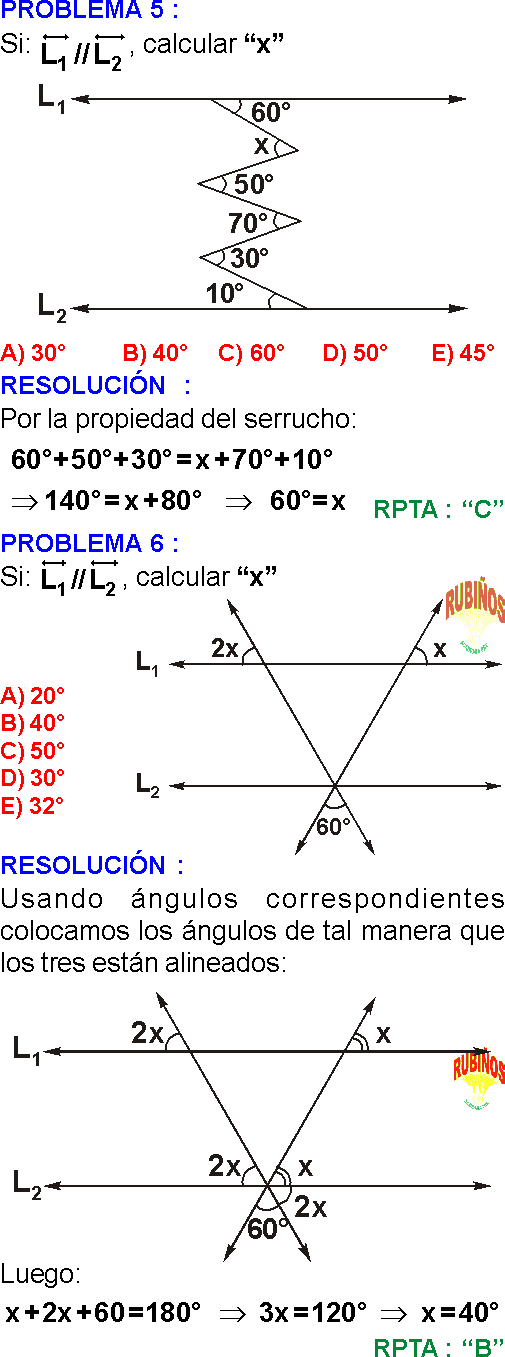
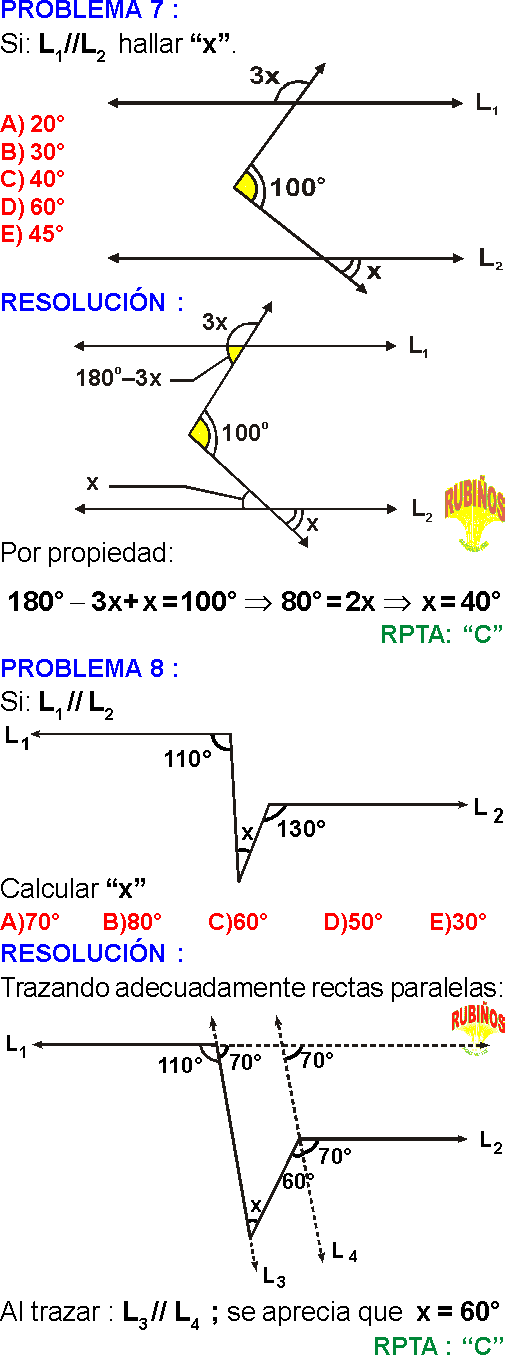
ÁNGULOS ENTRE PARALELAS EJEMPLOS Y PROBLEMAS RESUELTOS PDF
APRENDIZAJES ESPERADOS
En este capítulo aprenderemos:
• A definir y graficar dos rectas paralelas.
• A reconocer los ángulos alternos internos entre dos rectas paralelas.
• A plantear las propiedades correspondientes a los ángulos alternos internos.
• A reconocer los ángulos correspondientes determinados entre dos rectas paralelas.
• A plantear las propiedades relacionadas a los ángulos correspondientes.
• A aplicar las propiedades dadas a ángulos alternos internos.
• A aplicar las propiedades dadas a ángulos correspondientes.
• A desarrollar diversos problemas sobre ángulos determinados por rectas paralelas.
• A desarrollar diversos problemas.
OPERACIONES ENTRE ÁNGULOS DETERMINADOS POR RECTAS PARALELAS
La valla es un elemento superficial vertical que se utiliza para delimitar terrenos y protegerlos contra intrusos. Suelen ser de madera o metálicas.
Las vallas se colocan alrededor de un terreno o jardín y tienen la función de impedir la entrada al mismo o de proteger la intimidad de sus habitantes.
Las vallas se instalan en granjas, terrenos agrícolas o en otros espacios privados como, por ejemplo, los jardines de las viviendas unifamiliares.
Una valla clásica está formada por una serie de tablones o estacas de madera colocados en vertical y terminados en punta o de forma redondeada.
Los tablones se clavan al terreno y se unen por medio de otras tablas horizontales que se clavan a las anteriores.
Existen también vallas metálicas que consisten en una malla de alambre, denominada alambrada. También se encuentran vallas confeccionadas con materiales naturales como cañas o brezo. En este caso, las piezas se trenzan con alambre conformando una superficie tupida.
EL PARTENÓN
El diseño del Partenón estuvo condicionado inicialmente para albergar la imagen de oro y marfil de Atenea Parthenos, esculpida por Fidias.
La colosal estatua de doce metros de altura precisaba de una inmensa cella de más de 18 metros de anchura, dividida en tres naves mediante una doble columnata conformada por dos órdenes superpuestos de estilo dórico.
La nave central medía diez metros de anchura. Dentro de la cella del lado este, la columnata se dispuso en forma de "U" y estaba compuesta por nueve columnas con un entrepaño entre cada una de ellas, en los lados largos de la "U". Tres columnas con dos entrepaños formaban el lado corto.
En la zona oeste, al fondo del interior de la columnata de cuatro columnas, existía el basamento de la estatua, para el culto a Atenea Parthenos con un amplio estanque, poco profundo, que producía un efecto de brillo mediante el agua frente a ésta.
Ambas cellas estaban cerradas por puertas de bronce. La cella del este estaba dedicada a Atenea Polías (protectora de la ciudad), y la cella del oeste estaba dedicada a Atenea Párthenos, "la virgen", por lo cual todo el edificio acabó siendo conocido como el Partenón.
La decoración escultórica del Partenón es una combinación única de las metopas (esculpidas en altorrelieve extendiéndose por los cuatro lados externos del templo), los tímpanos (rellenando los espacios triangulares de cada frontón) y un friso (esculpido en bajorrelieve abarcando el perímetro exterior de la cella).
En ellos se representan varias escenas de la mitología griega. Además, las diversas partes del templo estaban pintadas de colores vivos.
El Partenón es, sin duda, el máximo exponente del orden dórico, como se puede apreciar en el diseño del friso o sus columnas.
• Desde la antigüedad ya se conocía el concepto de paralelismo , ¿las columnas del Partenón son paralelas?
La figura muestra un detalle del plano de construcción de una casa...
a) En el diseño de la escalera se dibujaron líneas auxiliares.
¿Cuál es el grupo de estas líneas?
b) ¿Dónde se presentan ángulos del mismo tamaño en el diseño de la escalera?
c) En el corte del escalón a la derecha, ¿dónde se presenta otro ángulo que mida igual que el ángulo "a"?...i dos rectas "L1" y "L2" son cortadas por una tercera recta "L" (secante), podemos nombrar parejas de ángulos según su posición de la siguiente manera:
Ángulos correspondientes: “a” y “e”; “d” y “h”; “b” y “f”; “c” y “g” Ángulos alternos internos: “d” y “f”; “c” y “e” Ángulos alternos externos: “a” y “g”; “b” y “h” Los ángulos alternos "alternan" el lado de la secante y "alternan" la recta paralela y su ubicación en ella. 1. Dibuja dos rectas paralelas "g" y "h", cortadas por una tercera recta "s". Denota todos los ángulos e indica los pares de ángulos correspondientes y todos los pares de ángulos alternos. 2. En la figura mostrada, las rectas "g" y "h" son paralelas entre sí. Calcula todos los ángulos, si: z = 110º... 3. Indica todos los pares de ángulos correspondientes y de ángulos alternos; calcula la medida de los ángulos denotados, todo basándote en los ángulos de la siguiente figura; además: g//h y a=30° y a = 30°. 4. Basándote en la figura, indica todos los pares de ángulos correspondientes y todos los pares de ángulos alternos con las rectas "L1" y "L2" así como con las rectas "L3" y "L4"