ECUACIÓN GENERAL DE LA RECTA Y ÁNGULO ENTRE 2 RECTAS PENDIENTE EJERCICIOS RESUELTOS PDF
Al finalizar del capítulo serás capaz de :
✎ Calcular la pendiente de la curva
✎ Uso de la ecuación general de la recta en situaciones geométricas.
✎ Calcular la pendiente de una recta.
✎ Determinar la ecuación general de la recta
✎ Cálculo de la ecuación de la recta.
✎ Determine la ecuación general de una recta paralela y perpendicular.
*
PROBLEMAS PROPUESTOS
PROBLEMA 1 :
Calcular la ecuación de una recta que pasa por los puntos (4; – 3) y (7;9).
A) x – y – 8 =0
B) 4x – y – 19 = 0
C) x = y
D) x – y + 8 =0
E) 4x+ y – 19 = 0
Rpta. : "B"
PROBLEMA 2 :
Determinar la ecuación de la recta que pasa por el punto medio del segmento que une los puntos (2;0) y (6;–2), y es perpendicular a este segmento.
A) y = x + 9
B) y = 2x 6
C) y = x – 5
D) y = 2x – 9
E) y = 2x – 8
Rpta. : "D"
PROBLEMA 3 :
Dos rectas se intersectan formando un ángulo de 135°, sabiendo que la recta final tiene pendiente igual a – 3. Calcular la pendiente de la recta inicial.
A) 1
B) 2
C) 3
D) 4
E) –1/2
Rpta. : "E"
PROBLEMA 4 :
Los vértices de un triángulo son los puntos A=(2;6); B(3;7) y C(5,9), halle la ecuación de la recta que contiene a la mediana relativa al lado BC.
A) x – y+ 4=0
B) x + y+ 4=0
C) x – y – 4= 0
D) x – y + 2 = 0
Rpta. : "A"
PROBLEMA 5 :
Calcular la distancia de la recta 3x+4y+4 =0, al punto (1; 2).
A) 1
B) 2
C) 3
D) 5
E) 7
Rpta. : "C"
PROBLEMA 6 :
Los vértices de un triángulo son los puntos A = (– 2;1); B=(4;7); C=(6;– 3).
Halle la ecuación de la recta que contiene a la altura BH.
A) 2x – y – 1 = 0
B) x + y+ 7 = 0
C) x – y+2=0
D) 3x + y – 1 = 0
E) 2x + y+ 10 = 0
Rpta. : "A"
PROBLEMA 7 :
Calcular la ecuación de la recta que pasa por el punto (2;3) y es perpendicular a la recta :
3x – 4y + 8 = 0
A) 4x + 3y – 17 = 0
B) 3x – y + 1 = 0
C) 3x + 4y + 17 = 0
D) 3x +y + 1 = 0
Rpta. : "A"
PROBLEMA 8 :
Si A(7;9), B(– 5; – 7) y C(12 ; – 3) son los vértices de un triángulo , entonces la ecuación de la mediatriz del lado AB es:
A) 3x + 4y + 7 = 0
B) 3x + 4y – 7 = 0
C) 3x – 4y + 7 = 0
D) 3x+4y – 7 = 0
Rpta. : "B"
PROBLEMA 9 :
Calcular la ecuación de mediatriz del segmento cuyos extremos son: A(1; – 4) y B(– 5;6)
A) 3x – 5y + 11 = 0
B) x + y – 5 = 0
C) x – 5y = 0
D) x + y = 0
E) x + y + 5 = 0
Rpta. : "A"
PROBLEMA 10 :
Dos vértices de un triángulo son los puntos (– 10;2) y (6;4). Si el ortocentro del triángulo es el punto (5;2), entonces las coordenadas del tercer vértice del triángulo es :
A) (4; – 4)
B) (5; – 5)
C) (6; – 6)
D) (7; – 7)
E) (8; – 8)
Rpta. : "C"
PROBLEMA 11 :
Halle la ecuación de una recta que intercepta el eje positivo de las x un segmento de longitud igual a 7, que pase además por el punto de abscisa x=4, perteneciente a la recta :
5x + 3y = 30
A) 10x – 9y+70 = 0
B) 9x + 10y – 70 = 0
C) 10x + 9y – 70 = 0
D) 9x – 10y + 70 = 0
Rpta. : "C"
PROBLEMA 12 :
Se tiene las ecuaciones de las rectas
ℒ1 : 3x + 2y – 18 = 0
ℒ2 : 3x + 2y – 12 = 0
Halle la ecuación de la recta ℒ3 que equidista de la recta ℒ1 y ℒ2
A) 3y+2y – 12=0
B) 3x+2y+15=0
C) 3y+2y – 8=0
D) 3x+2y+12=0
E) 3x+2y – 15=0
Rpta. : "E"
PROBLEMA 13 :
Dados los puntos A(3;4) y B(– 5;2), hallar la ecuación del lugar geométrico de todos los puntos que equidistan de los puntos A y B.
A) y=–4x– 1
B) y = 3x – 1
C) y = 4x + 2
D) y = 4x + 3
Rpta. : "A"
PROBLEMA 14 :
Se desea hallar la ecuación de una recta, que interceptando sobre el eje positivo de las x un segmento de longitud igual a 7 unidades, pasa además por el punto de abscisa x = 4 ; 5x+3y = 30 .
A) 10x+9y – 70= 0
B) 9x+10y – 70 = 0
C) 10x + y – 60 = 0
D) x + 9y –70 = 0
Rpta. : "A"
PROBLEMA 15 :
Se tiene el rombo ABCD, donde A =(2;2) y C= (4;6). Calcule la ecuación de la recta que contiene a la diagonal BD.
A) x + 2y – 3 = 0
B) x + 2y – 7 = 0
C) x + 2y + 11 = 0
D) x +2y – 11 = 0
E) x + y – 3 = 0
Rpta. : "D"
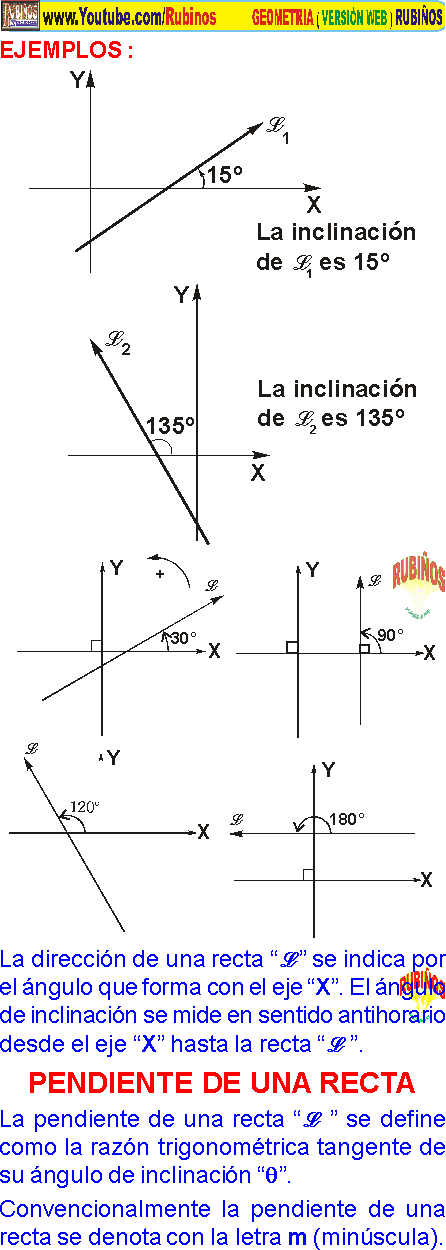
inclinacion de una recta ejercicio resuelto de geometria analitica , inclinacion de una recta problema resuelto de geometria analitica , pendiente de una recta - comprobacion , pendiente de una recta ejercicio resuelto , calculo de la pendiente de una recta - demostración , calculo de la pendiente de una recta - ejercicio resuelto , calculo de la pendiente de una recta - pregunta resuelta , calculo de la pendiente de una recta - problema resuelto , calculo de la pendiente de una recta - problema resuelto de nivel uni , ecuacion de la recta de su forma punto y pendiente ejercicio resuelto , ecuacion de la recta de su forma punto y pendiente problema resuelto , ecuacion de la recta - pendiente y ordenada al origen - su demostración , ecuacion de la recta - pendiente y ordenada al origen - ejercicio resuelto , ecuacion de la recta - pendiente y ordenada al origen - problema resuelto , la recta - propiedad de las pendientes entre dos rectas paralelas , la recta - propiedad de las pendientes entre dos rectas perpendiculares y su demostracion , ecuacion simetrica de la recta y su demostracion , ecuacion simetrica e la recta - ejercicio resuelto , ecuacion simetrica de la recta problema resuelto , ecuacion general de la recta y su pendiente ejercicio resuelto , ecuacion general de la recta problema resuelto , distancia de un punto hacia una recta -ecuacion de la recta ejercicio resuelto , distancia entre dos rectas paralelas ecuacion de la recta ejercicio resuelto , distancia entre dos rectas paralelas ecuacion de la recta problema resuelto , distancia entre dos rectas paralelas ecuacion de la recta problema resuelto de nivel uni ,


































































.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)

