ECUACIÓN DE LA RECTA PROBLEMAS RESUELTOS DE GEOMETRÍA ANALÍTICA ESCALAR PDF
OBJETIVOS
► Calcular la pendiente de una recta mediante distintos métodos
► Comprender la importancia de la pendiente para conocer la ecuación de una recta.
► Resolver problemas tipo exámenes de admisión.
¿Qué se entiende por pendiente?
¿Cómo calculo la inclinación?
¿Cómo calculo la pendiente?
PREGUNTA 1 :
Los vértices del triángulo rectángulo ABC son los puntos A = (–5 ; 5), B =(1;1) y C=(3;4). Determinar la ecuación de la recta que pasa por los puntos medios de los catetos de este triángulo.
A) 8y = 22 – x
B) 8y = 22 + x
C) 8y = 26 – x
D) 8y = 26 + x
E) 6y = 7 + 4x
Rpta. : "A"
PREGUNTA 2 :
Calcular la ecuación de la recta. cuyos puntos equidistan de las rectas:
ℒ1 : 12x – 5y + 20 = 0
ℒ2 : 12x – 5y –10 = 0
A) 5x – 12y + 5 = 0
B) 3x – y +7 = 0
C) 12x – 5y + 5 = 0
D) 3x+ y +7 = 0
Rpta. : "C"
PREGUNTA 3 :
Dado el vértice A(1; – 2); B(2;3) y C( – 2;1) son los vértice del triángulo mediano del triángulo MNP. Halle la suma de la abscisa y de la ordenada de uno de los vértices del triángulo MNP.
A) – 7
B) – 3
C) – 2
D) 0
E) 4
Rpta. : "A"
PREGUNTA 4 :
Si un punto sobre la recta 3x +5y =15 equidista de los ejes coordenados, entonces el punto mencionado puede encontrarse:
A) En ninguno de los cuadrantes.
B) En el cuadrante I solamente.
C) Solamente en los cuadrantes I y II.
D) Únicamente en los cuadrantes I, II y III.
E) En cada uno de los cuadrantes.
Rpta. : "C"
PREGUNTA 5 :
El área de una región rectangular ABCD es 50u², si las coordenadas de B y C son (1;4) y (9;–2) respectivamente , halle las coordenadas positivas del vértice A.
A) (3; 8)
B) (2; 8)
C) (4; 8)
D) (4;10)
E) (2;10)
Rpta. : "C"
PREGUNTA 6 :
Sea ABC un triángulo rectángulo isósceles , si las coordenadas de la hipotenusa A y B son (3; 4) y (9;12) respectivamente ,halle las coordenadas del tercer vértice.
A) (5;10)
B) (10;5)
C) (2;5)
D )(11;2)
E) (5;11)
Rpta. : "B"
PREGUNTA 7 :
Sean las rectas :
ℒ1 : x – y–2=0
ℒ2 : x – 2y – 1=0
ℒ3 con pendiente m>1.
Si ℒ1 es la bisectriz del ángulo formado por ℒ2 y ℒ3 halle m.
A) 5/4
B) 2
C) 5/2
D) 3
E) 4
Rpta. : "B"
PREGUNTA 8 :
Dado los vértices de un triángulo A(–10;–13), B(–2;3), C(2; 1) .
La longitud de la perpendicular trazada del vértice B a la mediana CM mide (en u):
A) 2
B) 3
C) 4
D) 5
E) 6
Rpta. : "C"
PREGUNTA 9 :
Dado el triángulo ABC, A=(0;2); 8=(4;14) y C=(13;2). Halle la ecuación de la recta de Euler de dicho triángulo .
A) 5x+3y – 10=0
B) 5x – 3y+10=0
C) 5x – 3y+5=0
D) 3x–5y+13=0
E) 3x – 5y–13=0
Rpta. : "D"
PREGUNTA 10 :
El punto A(3;9) es uno de los vértices del triángulo ABC y las ecuaciones de dos de sus medianas son
ℒ1 : y – 6 =0
ℒ2 : 3x – 4y + 9 =0
Determine las coordenadas de los otros dos vértices.
A) B (4 ; 6) y C(2; 4)
B) B (1 ; 6) y C(3; 2)
C) B (6 ; 6) y C(1; 1)
D) B (11; 6) y C(1; 3)
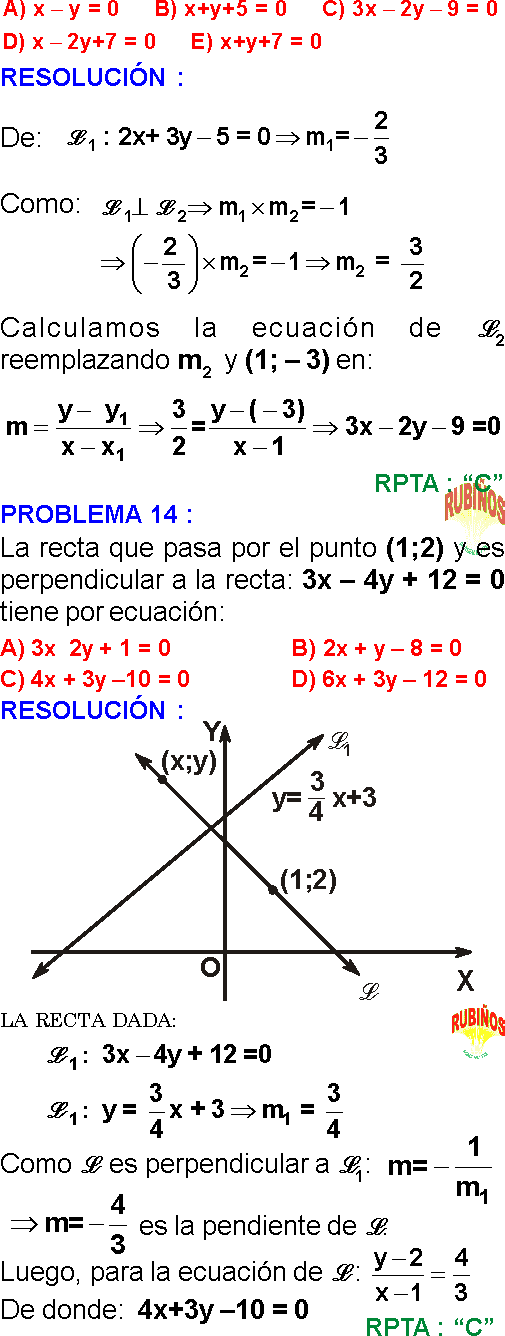
Rpta. : "D"