ÁNGULOS EN POSICIÓN STANDAR REGULAR CANÓNICA NORMAL Y DE CUALQUIER MEDIDA PROBLEMAS RESUELTOS DE RAZONES TRIGONOMÉTRICAS TRIGONOMETRÍA DE SECUNDARIA Y PREUNIVERSITARIA
Al finalizar estarás en capacidad de :
✎ Entender el uso de los sistemas de referencia como el sistema de coordenadas rectangulares o plano cartesiano.
✎ Definir las razones trigonométricas en el Plano Cartesiano.
✎ Calcular el valor de las razones trigonométricas de un ángulo en posición normal, conociendo un punto de su lado final.
✎ Determinar las razones trigonométricas para todo tipo de ángulos.
✎ Determinar el significado de las razones trigonométricas en el Plano Cartesiano.
✎ Aplicar conceptos básicos de Geometría Analítica.
✎ Reconocer los signos de las razones trigonométricas, según la posición del ángulo.
✎ Realizar operaciones con las razones trigonométricas de aplicaciones con enunciados.
✎ Calcular y aplicar los valores de los ángulos cuadrantes.
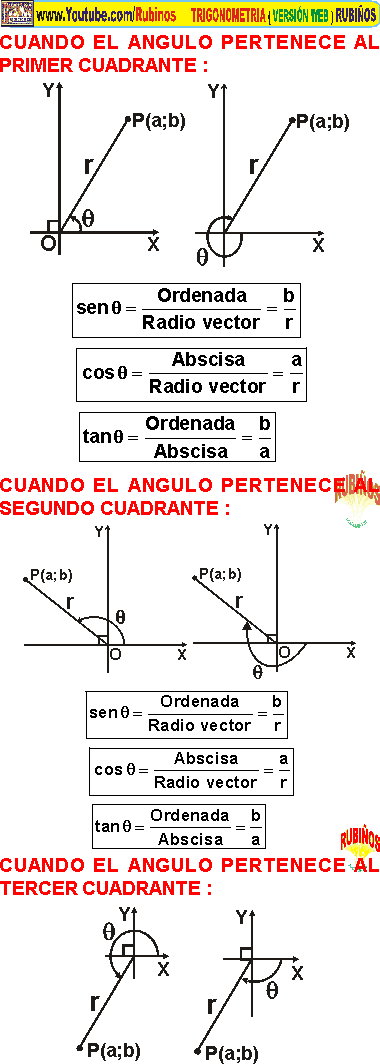
ÁNGULO EN POSICIÓN NORMAL
Llamado también ángulo en posición estándar, en posición regular o ángulo canónico.
Es aquel ángulo trigonométrico cuyo vértice coincide con el origen de coordenadas, el lado inicial coincide con el semieje positivo de abscisas y su lado final se ubica en cualquier parte del plano cartesiano.
Si el lado final de un ángulo en posición normal cae en uno de los cuadrantes del plano, se dice que ese ángulo pertenece a dicho cuadrante. Pero si el lado final coincide con uno de . los semiejes del plano, entonces es un ángulo . cuadrantal.
ÁNGULOS CUADRANTALES
Son aquellos ángulos que ubicados en posición normal tienen su lado final coincidente con cualquiera de los semiejes del plano cartesiano.