GEOMETRÍA BANCO DE PREGUNTAS RESUELTAS 2024 DE EXAMEN ADMISIÓN PDF
PREGUNTA 1 :
Sean los puntos consecutivos y colinelaes A, B, C y D; tales que:
BC= AB + 2
CD= AB – 4
Si AB toma su mínimo valor entero, halle AD
A) 14
B) 15
C) 13
D) 20
E) 18
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 2 :
Calcule el área de la región sombreada si AOB es cuadrante de centro O, OC=5m
A) 10𝛑 m2
B) 12𝛑 m2
C) 14𝛑 m2
D) 15𝛑 m2
E) 18𝛑 m2
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 3 :
Calcule en la figura, A, O y D son colineales. Halle y cuando x toma su máximo valor entero.
A) 53°
B) 59°
C) 56°
D) 60°
E) 50°
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 4 :
En la figura, AB=BC y CD=AB√2. Halle x.
A) 172°
B) 153°
C) 165°
D) 160°
E) 170°
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 5 :
El perímetro de un triángulo rectángulo es 48 m y su hipotenusa mide 20 m. Hallar la longitud de su inradio.
A) 4 m
B) 5 m
C) 6 m
D) 2 m
E) 3 m
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 6 :
En el lado AC del triángulo ABC se toma el punto D tal que AD= 6, DC= 8. Si la longitud de la perpendicular DH bajada al lado BC es 4, entonces la longitud de la altura del triángulo bajada desde el vértice A al lado BC es:
A) 5
B) 6
C) 7
D) 8
E) 9
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 7 :
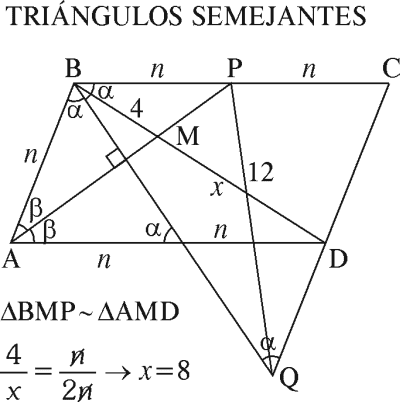
En un romboide ABCD, BC=2AB. La bisectriz de B interseca a la prolongación de CD en Q y la bisectriz de A interseca a BD en M y a BC en P. Si MB=4 cm y PQ=12 cm, halle MD en cm.
A) 9
B) 14
C) 12
D) 10
E) 8
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 8 :
En la figura adjunta, se tiene AB=7 cm, BF=5 cm y AD=4 cm. Halle el valor de DE.
A) 2 cm
B) 1 cm
C) 7cm
D) 5/3 cm
E)3 cm
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 9 :
Calcular el área (en cm²) de la región comprendida entre un círculo y el triángulo inscrito a este, de lados: 7 cm, 24 cm y 25 cm (considere 𝜋 = 3).
A) 468,75
B) 384,75
C) 256,14
D) 318,25
E) 418,32
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 10 :
¿Cuántos lados tiene un polígono convexo, si al duplicar su número de lados, el número de diagonales aumenta en 84?
A) 9 lados
B) 12 lados
C) 10 lados
D) 8 lados
E) 11 lados
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 11 :
La diferencia de la suma de las medidas de los ángulos internos de dos polígonos convexos es 1080°. Halle la diferencia de los números de lados de dichos polígonos.
A) 8
B) 4
C) 7
D) 5
E) 6
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 12 :
Hallar la distancia entre los puntos, cuyas coordenadas son: (0; 3) y (–4; 1).
A) 2√3
B) 2√5
C) 3
D) 5
E) 3√2
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 13 :
En un triángulo isósceles ABC donde AB=BC, sobre los lados AC, BC se ubican los puntos F y D, respectivamente, tal que BF=BD. Si el ángulo ABF = 40°, entonces, la medida del ángulo CFD, en grados sexagesimales, es
A) 10
B) 15
C) 20
D) 30
E) 40
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 14 :
En la figura, AB//CD, AB=DE y CD=AB+BE. Halle m∠BCE.
A) 18°
B) 25°
C) 10°
D) 15°
E) 20°
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 15 :
En la figura se tiene AB=CF, BC=AC=CD, halle 2x.
A) 40°
B) 53°
C) 37°
D) 45°
E) 60°
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 16 :
En la figura, ABCD es un cuadrado, donde AP=AQ. Halle el valor de x.
A) 37°
B) 45°
C) 53°
D) 60°
E) 30°
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 17 :
En la figura adjunta, ABC es un triángulo equilátero y α es 100°. Halle el valor de β
A)10°
B) 20°
C) 40°
D) 30°
E) 15°
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 18 :
En la figura, O es centro de la circunferencia, OM = SN. Halle x.
A) 17°
B) 14°
C) 15°
D) 13°
E) 16°
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 19 :
Un cuadrilátero inscrito en una circunferencia tiene tres lados iguales, cada uno de los cuales subtiende un arco de 60°. Halle la suma de las medidas del mayor y menor ángulo interno del cuadrilátero.
A) 240°
B) 180°
C) 160°
D) 150°
E) 210°
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 20 :
En la figura, ABCD es un cuadrado, E y T son puntos de tangencia. Si O y O1 son centros, halle la medida del arco FT.
A) 53°
B) 45°
C) 30°
D) 37°
E) 60°
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 21 :
Un cuadrilátero ABCD está circunscrito a una circunferencia, m∠A=90° y T es punto de tangencia en BC; si AD=15 cm, DC=24 cm y CT=18 cm, halle la medida del radio de la circunferencia.
A) 7 cm
B) 6 cm
C) 9 cm
D) 10 cm
E) 8 cm
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 22 :
En una circunferencia de radio 12m se traza una cuerda PQ, siendo la medida del arco PQ=60°. Hallar la longitud del arco PQ.
A) 4𝛑 m
B) 6𝛑 m
C) 8𝛑 m
D) 5𝛑 m
E) 7𝛑 m
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 22 :
En un triángulo ABC, se traza la altura BH relativa a AC (H en AC). Si AB+BC=16 cm, halle el máximo valor entero de BH.
A) 10 cm
B) 6 cm
C) 9 cm
D) 8 cm
E) 7 cm
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 23 :
En un triángulo ABC, m∠A=m∠C=30° y AC=6 m. Halle la distancia del circuncentro del triángulo ABC al excentro relativo al lado BC.
A) 2√2 m
B) 2√3 m
C) 3√6 m
D) 2√6 m
E) 3 m
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 24 :
En la figura adjunta, M, N y P son puntos de tangencia; O y O' son centros de las circunferencias. Si PM= 2PN, halle el valor de r'/r.
A) 3
B) 2
C) 4
D) 6
E) 5
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 25 :
En la figura, AF= 15 cm, FB= 6 cm, AC= 4 cm y BE= EC. Halle el valor de CD.
A) 7/3 cm
B) 5 cm
C) 9 cm
D) 4 cm
E) 8/3 cm
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 26 :
En un triángulo rectángulo ABC, se traza MN, M en AB y N en BC, si AM=12 cm y NC= 6 cm, halle la distancia entre los puntos medios de MN y AC.
A) 3√3 cm
B) 4√5 cm
C) 5√5 cm
D) 3√5 cm
E) 4√3 cm
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 27 :
En la figura, AB // CD y AD // BC, las áreas de las regiones triangulares BTF y ATD son 16 cm² y 25 cm² respectivamente. Halle el área de la región ABCD
A) 89 cm²
B) 88 cm²
C) 85 cm²
D) 80 cm²
E) 90 cm²
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 28 :
En la figura, se tiene AM=MC, PC= 3NP y el área de la región triangular ABC es 48 m². Halle el área de la región sombreada MPC.
A) 10 m²
B) 11 m²
C) 12 m²
D) 14 m²
E) 15 m²
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 29 :
En la figura, O es punto medio del diámetro AC. Si las áreas de las regiones sombreadas son S1= 7 m² y S2= 41 m², halle el área del sector circular DOC.
A) 35 m²
B) 45 m²
C) 48 m²
D) 34 m²
E) 36 m²
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 30 :
En un trapezoide ABCD, se tiene: m∠A= 60°; AB = 16√3 cm, CD= 40√2 cm, y m∠D= 45°. Hallar la distancia del punto medio M de BC a AD.
A) 16 cm
B) 18 cm
C) 32 cm
D) 36 cm
E) 64 cm
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 31 :
En un triángulo rectángulo ABC, se traza la altura BH y la bisectriz interior AD que se intersecan en E. Si numéricamente (AD)(ED)=64, ¿cuál es el valor de BE?
A) 2√2
B) 2√3
C) 4√2
D) 3√2
E) 4√3
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 32 :
En la figura, AB = 4 cm, BC = 7 cm y AC = 9 cm, AM = MB. Halle MQ.
A) 2√3/5 cm
B) √3/5 cm
C) √3/3 cm
D) 4√3/5 cm
E) √2/5 cm
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 33 :
Por el vértice B de un rectángulo ABCD se traza una recta perpendicular a BD. Si los vértices A y C distan de dicha recta en 15 m y 10 m respectivamente, el área de dicha región rectangular, en m², es:
A) 125√6
B) 120√6
C) 110√6
D) 130√3
E) 135√3
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 34 :
Es un cuadrilátero ABC, el punto P divide al segmento AC en la razón 1/3 sobre 3 donde AP<PC. Si las áreas de las regiones triangulares ABD y BDC se miden 70 m² y 30 m², respectivamente, entonces el área de la región triangular PBD en m² es
A) 45
B) 44
C) 42
D) 40
E) 39
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 35 :
En un polígono regular ABCDEF... m∠ABD=90°. Halle el número de diagonales de dicho polígono.
A) 8
B) 12
C) 6
D) 10
E) 9
RESOLUCIÓN :
Rpta. : "E"
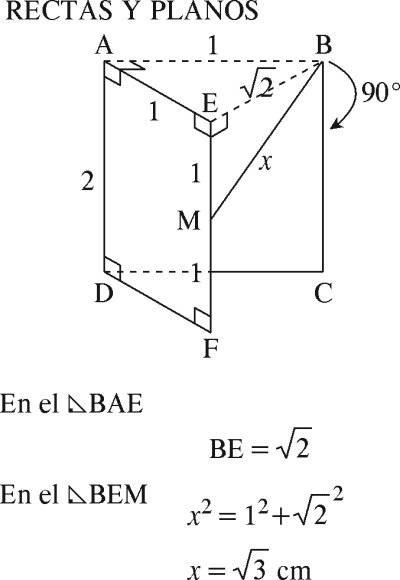
PREGUNTA 36 :
Hallar el radio de la circunferencia de centro O, si AB es perpendicular al plano P.
AF= 12; BO= 17; BA=9
A) 7
B) 17
C) 4
D) 8
E) 6
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 37 :
En la figuras, el triángulo rectángulo ABC está contenido en el plano H, mACB=53°/2 y AB=2 cm, D es un punto que no pertenece al plano H y DB es perpendicular al plano H, tal que DB=2 cm. Halle el área de la región triangular ADC.
A) 2 cm²
B) 3 cm²
C) 6 cm²
D) 30 cm²
E) 8 cm²
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 38 :
En la figura se muestra la vista frontal de una puerta ADFE de dimensiones AD = 2 cm, AE = 1 cm y EF = 2ME. Halle la medida de la cuerda tensada MB, tal que la puerta gire 90°.
A) √3 cm
B) 2√3 cm
C) 5 cm
D) 2√2 cm
E) 2 cm
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 39 :
La superficie lateral de un cilindro de revolución es una región cuadrada de área A. Hallar el volumen del cilindro en función de A.
A) (3A√A)/8𝜋
B) (A√A)/8𝜋
C) (A√A)/6𝜋
D) (A√A)/4𝜋
E) (A√A)/2𝜋
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 40 :
La base de una pirámide es un hexágono regular de √3 m de apotema. Si la altura es el doble del apotema de su base, entonces el volumen de dicho sólido, en m³, es
A) 8
B) 10
C) 12
D) 14
E) 16
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 41 :
Si la generatriz de un cono recto circular mide 5 m y la superficie lateral desarrollada forma un sector circular de 216°, entonces el volumen de dicho cono, en m³, es
A) 9𝛑
B) 10𝛑
C) 11𝛑
D) 12𝛑
E) 14𝛑
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 42 :
Si A(1;3) y B(2;–5) son los puntos extremos del segmento AB, halle la suma de las coordenadas del punto de trisección más próximo al extremo A.
A) –1/3
B) 5/3
C) –2/3
D) –5/3
E) 2/3
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 43 :
Las rectas
se intersecan formando una región triangular. Halle su área en m².
A) 4
B) 6
C) 3
D) 5
E) 2
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 44 :
Una recta pasa por el diámetro de la circunferencia
x² + y² – 6x + 4y –12 = 0 y biseca a la cuerda cuya ecuación es x+3y – 6= 0.
La ecuación de dicha recta es:
A) –2x+y –1=0
B) –x+3y –11=0
C) –2x+3y –11=0
D) 3x–y –11=0
E) 3x+2y – 6=0
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 45 :
Si las rectas
I₁ : x – 4y + 3 = 0
I₂ : 4x + y – 5 = 0
son tangentes a una circunferencia en los puntos P₁(5; 2) y P₂ (2; – 3) respectivamente, entonces la suma de las coordenadas del centro de la circunferencia es:
A) 3
B) 4
C) 5
D) 6
E) 7
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 46 :
La ecuación de la elipse es
La distancia del centro de la elipse a una cuerda AB paralela al eje mayor y de longitud a es
A) √3b/2
B) √5b/7
C) 3b/2
D) b/2
E) b/4
RESOLUCIÓN :
Rpta. : "A"
