LEYES DE KEPLER EJERCICIOS RESUELTOS DE INGRESO UNIVERSIDAD
EJERCICIO 1
Un escritor de ciencia ficción especula que la Tierra tiene un segundo satélite natural de igual masa que la Luna (Luna 2) y cuya órbita tiene un radio igual a la mitad del radio de la órbita de la Luna. Considerando que la Luna tiene un periodo de 28 días y que las lunas no interactúan, halle aproximadamente el periodo de la Luna 2 (en días).
A) 4,2
B) 5,6
C) 8,4
D) 9,9
E) 12,6
EJERCICIO 2
Dadas las siguientes proposiciones relacionadas con las leyes de Kepler.
I) Todos los planetas se mueven alrededor del Sol en trayectorias elípticas y planas, con el Sol en el centro de la elipse.
II) El radio vector trazado desde el Sol a un planeta barre áreas iguales en intervalos de tiempos iguales.
III) El periodo orbital de cualquier planeta es proporcional al cubo de la distancia media del planeta al Sol.
Indique la secuencia de verdad (V) o falsedad (F).
A) FVF
B) VVV
C) FVV
D) VFV
E) VFF
Resolución
Johannes Kepler, trabajando cuidadosamente con datos obtenidos por Tycho Brahe y sin la ayuda de un telescopio, describió el movimiento de los planetas en sus órbitas alrededor del Sol.
Primera ley: Los planetas se desplazan alrededor del Sol describiendo órbitas elípticas, en donde el Sol se ubica en uno de sus focos de la elipse.
Segunda ley: El radio vector que une un planeta y el Sol barre áreas iguales en tiempos iguales.
Tercera ley: El cuadrado de su periodo orbital es directamente proporcional al cubo de la distancia media del planeta al Sol.
Rpta. : "C"
PREGUNTA 3
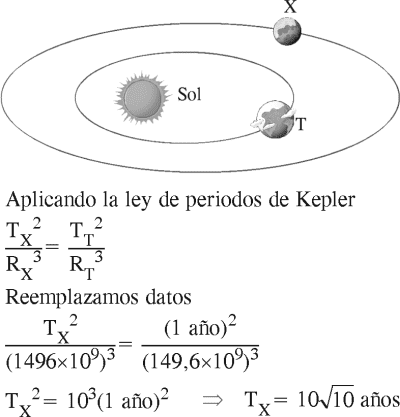
Se descubre un nuevo planeta X que orbita alrededor del Sol a una distancia media de 1496 millones de kilómetros. Calcule en años, el periodo medio con el que órbita el planeta X.
Considere que la distancia media de la tierra al Sol es 149,6 millones de kilómetros.
A) 1
B) 5
C) 5√5
D) 10
E) 10√10
Resolución
Rpta. : "E"
PREGUNTA 4
Dos satélites idénticos S1 y S2 orbitan circularmente alrededor de un mismo planeta. El primero tiene un periodo de 512 horas y el segundo de 343 horas Calcule la relación de los radios de sus órbitas R1/R2
A) 16/15
B) 8/7
C) 41/35
D) 56/42
E) 64/49
Resolución
Rpta. : "E"
EJERCICIO 5
El cometa Runrun se acerca al sol a una distancia mínima de 0,6U.A. y su período orbital es de 64 años. ¿Qué tan lejos del sol viajará el cometa Runrun antes de que inicie su viaje de regreso (en UA)?
1UA = 1,5×108 km: distancia media de la Tierra al Sol
A) 16
B) 32
C) 31,4
D) 32,6
E) 15,4
EJERCICIO 6
El satélite de comunicaciones Exit–sat se encuentra geoestacionario en un punto sobre el Ecuador y a una distancia R del centro de la Tierra. ¿Cuál es, aproximadamente, la distancia Tierra- Luna?. Considere que la Luna demora 27 días en orbitar alrededor de la Tierra.
A) 3R
B) 6R
C) 9R
D) 12R
E) 15R
EJERCICIO 7
El 30 de enero se observa un asteroide en su órbita alrededor del sol. Si después de 10 meses, el radio vector ha barrido el 20% del área de la región limitada por su órbita. Determine el periodo orbital del asteroide (en meses).
A) 50
B) 25
C) 100
D) 5
E) 10
EJERCICIO 8
Un planeta tiene 2 satélites A y B que giran a su alrededor describiendo órbitas aproximadamente circulares. Si el periodo de B es de 810 días y el radio de la órbita de A es la novena parte del radio de la órbita de B, calcule el periodo de A (en días).
A) 30
B) 15
C) 60
D) 90
E) 6
EJERCICIO 9
La distancias de dos satélites a un planeta son de r y 4r y el periodo del primero es de 20 días, determine el periodo del segundo satélite (en días).
A) 20
B) 40
C) 180
D) 120
E) 160
EJERCICIO 10
Un planeta M tiene 2 satélites (A y B) los que giran a su alrededor, describiendo órbitas aproximadamente circulares. Si el periodo de B es 160 días y el radio de la órbita de giro de A es la cuarta parte del radio de la órbita de B, calcular el periodo de A (en días).
A) 20
B) 10
C) 15
D) 40
E) 5
EJERCICIO 11
En el perihelio un planeta estuvo a 9×107km del centro del Sol y en el afelio está a 6×109km del Sol. Si en el perihelio su rapidez era 5,5×104 m/s, determine su rapidez en el afelio (en 102m/s)
A) 8,25
B) 1,45
C) 4,25
D) 22,36
E) 104,24
EJERCICIO 12
Una de las lunas de Júpiter, Ío, describe una órbita de radio medio 4,22×108 m y un periodo de 1,53×105 s. Calcule el radio medio (en m) de otra de las lunas de Júpiter, Calisto, cuyo periodo es de 1,44×106 s. Dato: (88,56)1/3 = 4,45
A) 2,34×107
B) 4,42×108
C) 1,87×109
D) 5,62×1010
E) 1,33×1011
EJERCICIO 13
Suponga que se ha descubierto un pequeño planeta en el sistema solar, su período de rotación alrededor del sol es de 5 años. ¿Cuál debe ser su distancia media al Sol en unidades astronómicas (en UA)?
Considere:
G = 6,67×10 – 11N·m2/kg2
Msol= 1,99×1030 kg
1UA = 1,5×1011 m: distancia media de la Tierra al Sol
A) 41/3
B) 161/3
C) 201/3
D) 251/3
E) 51/3
EJERCICIO 14
Si la distancia de mercurio a la tierra es el triple de la distancia de mercurio al sol, determine aproximadamente, ¿cuántos días terrestres dura el año en mercurio?
A) 21,8
B) 36,8
C) 45,6
D) 53,8
E) 69,4
LEYES DE KEPLER PRIMERA LEY (LEY DE LAS ÓRBITAS)
Los planetas describen elipses estando el Sol en uno de sus focos.
SEGUNDA LEY (LEY DE LAS ÁREAS)
Una línea desde el Sol hasta un planeta describe áreas iguales en intervalos de tiempo iguales.
TERCERA LEY (LEY DE LOS PERÍODOS)
El cuadrado del periodo de revolución de un planeta es directamente proporcional al cubo de la distancia promedio entre el planeta y el Sol.
