DILATACIÓN EJERCICIOS RESUELTOS PDF DILATACIÓN TÉRMICA LINEAL SUPERFICIAL Y VOLUMÉTRICA
PROBLEMA 1
Una lámina delgada de latón de 20°C tiene la misma superficie que una lámina delgada de acero a 10°C. Determine a qué temperatura común, ambas láminas tendrán la misma superficie. Se sabe que el coeficiente de dilatación lineal del latón es el triple del coeficiente de dilatación lineal del acero.
A) 50 °C
B) 75 °C
C) 25 °C
D) 30 °C
E) 15 °C
Resolución
Rpta. : "C"
PRACTICA
PREGUNTA 1 :
Calcular las longitudes en cm de una varilla de latón y de una varilla de hierro para que, tengan una diferencia de longitud constante de 5 cm a todas las temperaturas. Los coeficientes de dilatación lineal del latón y del hierro son 0,000018 por °C y 0,000012 por °C respectivamente.
A) 20; 15
B) 10; 15
C) 5;10
D) 25; 20
E) 20; 5
Rpta. : "B"
PREGUNTA 2 :
Escoja la verdad o falsedad de las siguientes proposiciones.
I) Se denomina dilatación térmica de un cuerpo a la variación de su tamaño debido a un cambio en su temperatura.
II)Las fuerzas en la dilatación de un cuerpo pueden ser tan intensas que estiran objetos duros como el acero.
III)Una barra de 50 m de longitud, de acero (αacero= 1,1 × 10–5 °C–1) se contrae en 2,75 cm, cuando su temperatura pasa de 100°C a 50°C.
A) VVV
B) FVV
C) VFV
D) VVF
E) FFF
Rpta. : "A"
PREGUNTA 3 :
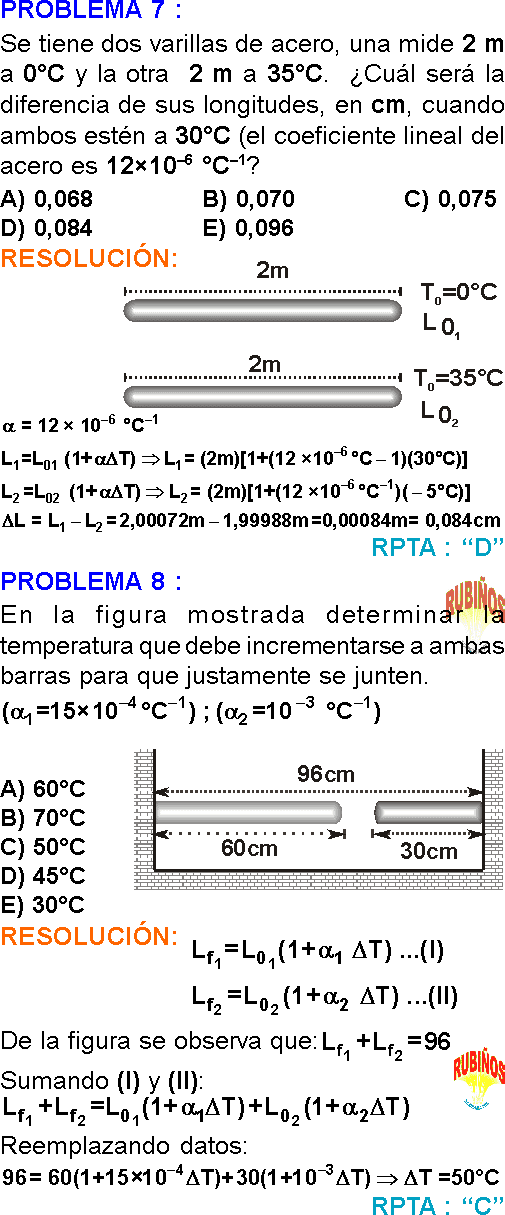
Se tiene dos varillas de acero, una mide 2 m a 0°C y la otra 2 m a 35°C. ¿Cuál será la diferencia de sus longitudes, en cm, cuando ambos estén a 30°C (el coeficiente lineal del acero es 12×1–6 °C–1?
A) 0,068
B) 0,070
C) 0,075
D) 0,084
E) 0,096
Rpta. : "D"
PREGUNTA 4 :
Un tubo de metal tiene una longitud de 1m a 20°C. Se hace pasar a través de él vapor de agua a 95°C y se observa que se alarga hasta 1,003 m. el coeficiente de dilatación líneal del metal es:
A) 10–5/°C
B) 4×10–5/°C
C) 4×10–3/°C
D) 10–3/°C
E) 2,5×10–3/°C
Rpta. : "B"
PREGUNTA 5 :
Se desea colocar un anillo de 2 cm de radio interno sobre un tubo de 2,1cm de radio externo, si inicialmente el anillo está a 25°C, ¿hasta qué temperatura, en °C, se le deberá colocar para que ingrese justo sobre el tubo? El coeficiente de dilatación superficial del material del cual está hecho el anillo es 0,002C–1.
A) 50
B) 125
C) 100
D) 76
E) 150
Rpta. : "D"
PREGUNTA 6 :
Una placa circular de área 20 cm² y coeficiente de dilatación lineal α=2,5×10–3 °C–1 experimenta un incremento de su temperatura en 200°C, determine su nueva área.
A) 50 cm2
B) 72 cm2
C) 20,2 cm2
D) 20,8 cm2
E) 16,8 cm2
Rpta. : "C"
PREGUNTA 7 :
A 15°C una rueda tiene un diámetro de 30cm y el diámetro interior de la llanta de acero es 29,96 cm.¿A qué temperatura debe calentarse la llanta para que pueda entrar en la rueda?
(αacero= 11×10–6 °C–1)
A) 100°C
B) 104°C
C) 136,4°C
D) 109°C
E) 120,5°C
Rpta. : "C"
PREGUNTA 8 :
Determine la relación entre las longitudes de dos varillas, una de cobre y otra de hierro, para que la diferencia de sus longitudes sea de 5cm a cualquier temperatura.
αCu = 16×10–6 °C–1 ; αhierro= 12×10–6 °C–1
A) 1
B) 2
C) 3
D) 3/4
E) 5
Rpta. : "D"
PREGUNTA 9 :
Una varilla de cobre de 3 m de longitud sujeta por un extremo y apoyada sobre rodillos de 1 cm de diámetro se calienta por acción de la corriente desde 20°C hasta 220°C, lo cual hace girar los rodillos. ¿Cuánto gira el último rodillo contado a partir del extremo fijo?
αCu = 17×10–6 °C–1
A) 117°C
B) 105°C
C) 102°C
D) 200°C
E) 98°C
Rpta. : "A"
PREGUNTA 10 :
El centro de una rueda de locomotora se tornea con un diámetro de 1,427 m y la llanta con un diámetro interior 1,423 m ambos a 15°C. Para colocar la llanta se calienta hasta 400°C. ¿Cuánto puede enfriarse mientras se efectúa la operación de colocarla?
(αFe=11,8×10–6 °C–1)
A) 120°C
B) 132°C
C) 143°C
D) 147°C
E) 181°C
Rpta. : "D"
PREGUNTA 11 :
Un volumen de 960 cm3 de Hg, (de coeficiente de dilatación cúbica = 0,00018°C–1), está dentro de un recipiente de 1000cm3 de capacidad (exacta) fabricado de un material de coeficiente de dilatación cúbica = 0,0000128/°C. Si se eleva la temperatura del conjunto de 0° a 250°C, entonces:
A) El Hg ocupa exactamente la capacidad del recipiente.
B) Se derrama 3,2 cm3 de Hg.
C) Se derrama más de 3,2 cm3 de Hg.
D) Es necesario añadir 3,2 cm3 de Hg para llenar totalmente el recipiente.
E) Queda aún un volumen vacío en el recipiente.
Rpta. : "A"
PREGUNTA 12 :
Un cubo metálico que en condiciones normales de presión y temperatura tiene una masa =79,45 kg, siendo su densidad 11,35 g/cm3 y su coeficiente de dilatación lineal igual a 2,8×10–5 °C–1, se coloca en un ambiente cuya temperatura es diferente y se comprueba que su nuevo volumen es 7058,8 cm3. Determine la temperatura del nuevo ambiente en °C.
A) 80
B) 100
C) 120
D) 140
E) 160
Rpta. : "B"
PREGUNTA 13 :
En cuánto debe variar la temperatura de una sustancia para que su densidad disminuya en el 0,1% considere γ=10–4 °C–1.
A) 5°C
B) 8°C
C) 12°C
D) 10°C
E) 25°C
Rpta. : "D"
PREGUNTA 14 :
El mercurio a 0°C tiene una densidad igual a 13600kg/m3, y un coeficiente de dilatación cúbica de 1,82×10–4 °C–1. La densidad del mercurio en kg/m3 a 20°C es entonces aproximadamente igual a:
A) 14 550
B) 91 35
C) 13 650
D) 13 550
E) 13 450
Rpta. : "D"
PREGUNTA 15 :
El período de un péndulo de hilo metálico es √10 , al descender la temperatura asume una frecuencia de 1/3 hertz. Encuéntrese el descenso de la temperatura. El hilo metálico tiene un coeficiente de dilatación lineal de 16×10–5 °C–1.
A) 720°C
B) 600°C
C) 724°C
D) 625°C
E) 800°C
Rpta. : "D"
PREGUNTA 16 :
A 0°C de temperatura y una atmósfera de presión la densidad del aluminio es 2,7 g/cm3 y su coeficiente de dilatación lineal es α=23×10–6 °C–1. Calcular la temperatura en °C a la cual su densidad disminuye en 1,0%
A) 116,4
B) 126,4
C) 136,4
D) 146,4
E) 156,4
Rpta. : "D"
PREGUNTA 17 :
Se construye un cubo de lado a=10 cm, con varillas metálicas, de tal manera que ante un cambio de temperatura de 100°C su volumen aumenta en 1/8, respecto al volumen correspondiente a la temperatura inicial. Entonces el coeficiente de dilatación lineal (en 1/°C) de las varillas es:
A) 1/8
B) 3/8
C) 1/24
D) 1/240
E) 1/2400
Rpta. : "E"
EJERCICIO 1
Un tubo de metal tiene una longitud de 1m a 20°C. Se hace pasar a través de él vapor de agua a 95°C y se observa que se alarga hasta 1,003m. El coeficiente de dilatación lineal (en 10–5 C°–1) del metal es:
A) 4,5
B) 2,5
C) 6
D) 5
E) 4
PROBLEMA 1
Un anillo de hierro debe ajustarse perfectamente en una barra cilíndrica de hierro. A la temperatura de 20°C el diámetro de la barra es 6,02 cm y el diámetro interior del anillo es 6 cm. Para deslizarse sobre la barra, el anillo debe ser ligeramente más grande que el diámetro de la barra en 0,02 cm.
¿Qué temperatura debe tener el anillo si su hoyo debe ser lo suficientemente grande para deslizarse sobre la barra?
αhierro=12×10–6 C°–1
A) 465,5°C
B) 385,5°C
C) 645,5°C
D) 575,5°C
E) 425,5 °C
Resolución
Rpta. : "D"
EJERCICIO 2
Un evaluador usa una cinta métrica de acero que tiene exactamente 50m de longitud a una temperatura de 20°C. ¿Qué longitud, en mm, se incrementa en un día caluroso de verano en el que la temperatura es de 35°C? a = 1,2 × 10–5 C°–1
A) 8
B) 7,5
C) 12,5
D) 9
E) 8,5
EJERCICIO 3
Por un tubo de metal (a = 4× 10–5 C°–1) cuya longitud es 1,003m, circula agua a 95°C. Calcular el porcentaje (%) que se dilató, si la temperatura ambiente es 20°C.
A) 0,5
B) 0,4
C) 0,3
D) 0,2
E) 0,1
EJERCICIO 4
La base de una plancha eléctrica es una placa de aluminio que tiene un área de 200cm2 a la temperatura de 20°C. Calcule en cuanto aumenta el área de dicha base (en cm2), si la temperatura de la plancha cuando está funcionando es 270°C. (aaluminio= 23×10 – 6 °C – 1)
A) 1,5
B) 2,3
C) 4,3
D) 1,8
E) 4,2
EJERCICIO 5
Dos alambres metálicos con coeficientes de dilatación lineal a1 y a2 (a1 < a2) tienen la misma longitud L0 a la temperatura T. Determine el valor necesario del incremento DT de la temperatura para que la diferencia entre sus longitudes sea L0/10.
A) 0,2(a2 – a1)
B) 0,5(a2 – a1)
C) a2 – a1
D) 0,4(a2 – a1)
E) 0,1(a2 – a1)
EJERCICIO 6
Se requiere que un cilindro de diámetro 1cm a 20°C pueda pasar a través de un hoyo en una placa de acero. El hoyo tiene un diámetro de 0,9997cm a 20°C. ¿A qué temperatura (en °C) debe calentarse la placa? aacero= 1,1×10 – 5 °C – 1
A) 47,3
B) 44,5
C) 39,7
D) 37,5
E) 51,5
EJERCICIO 7
Dos esferas metálicas con coeficientes de dilatación lineal a1 y a2 (a1 < a2) presentan el mismo volumen V0 a la misma temperatura T. Determine el valor del incremento en la temperatura (el mismo DT para ambas esferas) necesario para que la diferencia entre sus volúmenes sea V0/10. Considere que la dilatación es uniforme en todas sus direcciones.
A) a2 + a1
B) a2 – a1
C) [3(a2 – a1)]– 1
D) (a2 – a1)– 2
E) [30(a2 – a1)]– 1
EJERCICIO 8
Un frasco de vidrio (g = 1,2×10 – 5 °C – 1) de 0,5 litros se encuentra completamente lleno de un líquido, a 20°C. Al calentar el conjunto hasta 120°C, se derraman 10cm3 de líquido. ¿Cuál es su coeficiente de dilatación volumétrica (en 10 – 5 °C – 1)?
A) 21,2
B) 32,5
C) 24,3
D) 15,5
E) 18,2
EJERCICIO 9
Un frasco volumétrico hecho de pirex, se llena completamente con 100mL de acetona a 35°C ¿Qué volumen vacío, en mL, queda en el frasco cuando se enfría el sistema frasco – acetona a 20°C? apirex= 3,2×10 – 6 °C – 1 aacetona= 1,5×10 – 4 °C – 1
A) 0,25
B) 0,24
C) 0,23
D) 0,22
E) 0,21
EJERCICIO 10
Un recipiente de 1L de capacidad se llena completamente de mercurio a 20°C. Calcule el volumen (en cm3) de mercurio que se derramará si se calienta el recipiente hasta 100°C. Los coeficientes de dilatación volumétrica del mercurio y del material del recipiente son 1,8×10 – 4°C – 1 y 1,2×10 – 4°C – 1 respectivamente.
A) 1,2
B) 2,4
C) 4,8
D) 9,6
E) 14,4
EJERCICIO 11
Un recipiente de vidrio con 250cm3 de capacidad se llena completamente con mercurio a 20°C. ¿cuánto mercurio se derramará (en cm3) al calentar dicho recipiente hasta 100°C? Considerar, los coeficientes de dilatación volumétrica: vidrio: 1,2×10 – 5 °C – 1, mercurio: 18×10 – 5 °C – 1.
A) 3,95
B) 4,33
C) 2,15
D) 2,65
E) 3,36
EJERCICIO 12
Un anillo de cobre debe ajustarse fuertemente alrededor de un eje de acero cuyo diámetro es 5cm a 30°C. El diámetro interior del anillo de cobre a esa temperatura es de 4,98cm. ¿A qué temperatura (en °C) debe calentarse el anillo para que ajuste perfectamente sobre el eje de acero, suponiendo que éste permanece a 30°C? (Coeficiente de dilatación lineal del cobre=17×10 – 6 °C – 1).
A) 236,2
B) 306,2
C) 296,2
D) 266,2
E) 356,2
EJERCICIO 13
Un recipiente de vidrio cuya altura es de 8cm se llena con agua a 20ºC, faltando una altura de 0,5× 10 – 3m para llegar al borde del recipiente. ¿Hasta cuántos grados centígrados, aproximadamente, se debe calentar al recipiente con agua, para llegar al borde sin que se rebase del recipiente? No considere la dilatación del vidrio. Coeficiente de dilatación volumétrica del agua = 2,1×10 – 4 °C – 1
A) 30,38
B) 31,29
C) 40,30
D) 41,24
E) 49,95
EJERCICIO 14
El espacio de separación entre los rieles de acero de una línea ferroviaria es de 2cm. Cada riel tiene una longitud de 20m a temperatura ambiente (T=20°C). En estas condiciones, calcule la temperatura máxima en que puede dilatarse cada riel antes de doblarse. Dato: aacero= 11×10 – 6 °C – 1
A) 121°C
B) 105°C
C) 111°C
D) 134°C
E) 140°C
EJERCICIO 15
En relación con la dilatación de los sólidos, se dan las siguientes proposiciones:
I) La relación de variación de volumen vf= v0(1+gDT) es válido para cualquier intervalo de temperatura.
II) El coeficiente de dilatación volumétrica g (gamma) es aproximadamente dos veces el coeficiente de dilatación lineal.
III) El valor del coeficiente de dilatación volumétrica depende de la escala de temperatura empleada. Son correctas:
A) Sólo I
B) Sólo II
C) Sólo III
D) Sólo I y II
E) Sólo II y III
EJERCICIO 16
Los rieles por donde circulan los trenes se colocan con cierta separación entre ellos para evitar la deformación por los efectos de la dilatación debido a los cambios de temperatura. Si la temperatura durante un año fluctúa de 35°C en verano hasta – 40°C en invierno y los rieles son de acero con una longitud de 25m, ¿qué separación mínima debe existir entre dos rieles contiguos para que no se deformen (en cm)? Dato: aacero = 1,2× 10 – 5K – 1
A) 2,15
B) 4,50
C) 2,25
D) 3,25
E) 2,45
EJERCICIO 17
Al medir la densidad de un sólido de 1600cm3 a la temperatura de 10°C se obtiene 9g/cm3, cuando se mide a 30°C se encuentra que la densidad es 8989kg/m3. Calcule el coeficiente de dilatación volumétrica del sólido (en 10 – 5 °C – 1).
A) 4,93
B) 8,26
C) 7,75
D) 5,88
E) 6,12
EJERCICIO 18
La densidad del aluminio a 0°C es 2,7×103kg/m3. Calcule en 103 kg/m3 la densidad del aluminio a 200°C. Considere el coeficiente de dilatación térmica volumétrica del aluminio es 72×10 – 6 °C – 1.
A) 2,95
B) 3,25
C) 4,15
D) 1,65
E) 2,66
EJERCICIO 19
Si se mide la densidad de un sólido homogéneo a 10°C se obtiene 5g/cm3 siendo su volumen 160cm3. Cuando se mide a 30°C se encuentra que la densidad es de 4994 kg/m3. Calcule el coeficiente de dilatación volumétrico del sólido (en 10 – 5 °C – 1).
A) 4
B) 5
C) 6
D) 7
E) 8
EJERCICIO 20
Se tienen dos esferas huecas uniformes y concéntricas de radios a=10cm y b=30cm, donde ambas se encuentran a la misma temperatura, se desea calcular el coeficiente de dilatación lineal de la esfera de radio menor (en 10 – 5 °C – 1), sabiendo que el coeficiente de dilatación lineal de la otra esfera es 1,3×10 – 5 °C – 1. Además, se sabe que el volumen entre las esferas se mantiene constante.
A) 47,8
B) 44,5
C) 35,1
D) 47,5
E) 31,5
EJERCICIO 21
Una placa rectangular tiene un coeficiente de dilatación lineal de: 8 × 10– 5 °C– 1, al aumentar su temperatura en 100°C el aumento porcentual (en %) de la superficie es:
A) 1
B) 0,8
C) 0,84
D) 2
E) 1,6
EJERCICIO 22
Una plancha metálica de 2m×2m tiene un agujero central de área 0,8m2. Si su temperatura aumenta en 20°C, el área del agujero aumenta en 32cm2. Determine el incremento (en mm) en la longitud de la plancha.
A) 14
B) 10
C) 12
D) 6
E) 4
EJERCICIO 23
Al incrementar en 100°C la temperatura de una placa metálica rectangular, se encuentra que el área de su superficie se incrementa en 0,220%. Si inicialmente la diagonal medía 5m, ¿en cuántos milímetros se incrementará esta diagonal?
A) 5,5
B) 4,4
C) 6,3
D) 7,2
E) 4,1
EJERCICIO 24
A un cubo de cierto material tiene 10m de arista y coeficiente de dilatación volumétrica de g = 36×10 – 6 °C – 1, se le incrementa su temperatura en 100°C. Determine el incremento (en mm) de una de sus diagonales.
A) 20
B) 36
C) 18
D) 24
E) 34
EJERCICIO 25
Un reloj de péndulo está hecho de latón y tiene una longitud tal que a 20°C su periodo de oscilación es 1s. (aLatón= 2×10 – 5 °C – 1) Calcule, aproximadamente, en cuánto se atrasa (en s), este reloj en un día, si el ambiente donde se encuentra se mantiene a 30°C.
A) 7,64
B) 8,64
C) 9,64
D) 10,64
E) 11,64
Mediante el sentido del tacto podemos percibir cuál de dos cuerpos es el más caliente y cuál es el más frío, es decir, sabremos reconocer cuál tiene temperatura más elevada. En otras palabras, la temperatura de un cuerpo es una propiedad que se relaciona con el hecho de que un cuerpo esté "más caliente" o "más frío".
Suponga que tuviésemos dos cuerpos con distinta temperatura, uno en contacto con el otro y lejos de influencias externas.
Podría comprobarse que el cuerpo más caliente se iría enfriando, mientras que el más frío se iría calentando. Después de cierto tiempo se notaría, empleando el tacto, que los cuerpos alcanzan una misma temperatura.
A partir de este momento, las temperaturas de los cuerpos no sufrirán alteraciones, es decir, llegarán a una situación final denominada estado de equilibrio térmico. Un gran número de fenómenos que ocurren en nuestra vida diaria se relacionan con el de la dilatación.
Cuando calentamos un anillo, o en general, una placa con orificio, comprobamos que con la dilatación de la placa el orificio también incrementa su tamaño, dilatándose como si la placa estuviese entera, o sea, como si el orificio "estuviese hecho del mismo material que la placa".
Este hecho se utiliza en la adaptación de aros metálicos a ruedas de madera (en las carretas, por ejemplo), del siguiente modo; el aro o llanta, de diámetro ligeramente menor que el de la rueda, se calienta primero y es posible así encajar luego la rueda en él.
Cuando el aro retorna a la temperatura ambiente, se contrae y queda sujeto firmemente a la periferia de la rueda. Lo mismo sucede con la dilatación volumétrica. La capacidad de un recipiente cualquiera aumenta cuando se eleva su temperatura, debido a la ampliación de la parte hueca (volumen interno) del recipiente.
La temperatura ambiente en casi todos los lugares de la Tierra, sufre cambios considerables del día a la noche, de estación en estación, etc. De manera que en los objetos existentes en esos lugares obviamente se alterarán periódicamente sus dimensiones. Para permitir que las dilataciones y contracciones térmicas se produzcan sin daño, en las vías de los ferrocarriles o en las grandes estructuras metálicas o de concreto armado.
¿QUÉ ES LA DILATACIÓN ?
Es el fenómeno físico por efecto del calor que consiste en el cambio de dimensiones que experimenta un cuerpo, al aumentar o disminuir sus distancias intermoleculares, cuando varía su temperatura.
DILATACIÓN LINEAL
Es el cambio de longitud que experimenta un cuerpo que tiene una dimensión como principal, debido al cambio de temperatura.
El cálculo del coeficiente de dilatación adquiere una gran importancia en materiales continuos, uno de ellos son los carriles del ferrocarril.
Estos carriles van soldados unos con otros por lo que pueden llegar a tener una longitud de varias decenas de miles de metros.
Si la temperatura aumenta mucho la vía férrea se desplazaría por efecto de la dilatación, deformando completamente el trazado. Para evitar esto, se estira el carril artificialmente, tantos centímetros como si fuese una dilatación natural y se corta el sobrante, para volver a soldarlo. A este proceso se le conoce como neutralización de tensiones.
DILATACIÓN SUPERFICIAL
Es el cambio de área que experimenta un cuerpo que tiene dos dimensiones como principales, debido al cambio de temperatura.
DILATACIÓN CÚBICA
Es el cambio de volumen que experimenta un cuerpo debido al cambio de temperatura. Se da para todo cuerpo que posee tres dimensiones.
VARIACIÓN DE LA DENSIDAD CON LA DILATACIÓN
La expresión que define la densidad de un cuerpo esta en función a su masa y su volumen, dado que un cuerpo sometido a variaciones de temperatura sufre incrementos en su volumen es obvio que durante un proceso térmico la densidad de dicho cuerpo no se mantendrá constante.
PROPIEDADES DE LA DILATACIÓN
I) Si existe una cavidad en el interior de un cuerpo, ésta se dilata como si fuera parte del cuerpo.
II) En la dilatación, cuando el volumen aumenta, la densidad y el peso específico disminuyen. La masa permanece constante.
III) La fórmula de dilatación cúbica es válida para cuerpos sólidos y líquidos, mientras que las fórmulas de dilatación lineal y superficial son válidas únicamente para cuerpos sólidos.
La dilatación de los gases no obedece a ninguna de estas fórmulas.
ALGUNOS ALCANCES SOBRE LA DILATACIÓN TÉRMICA
Considerar la dilatación de los cuerpos es, con frecuencia, un problema fundamentalmente técnico. Si tratáramos de impedir la dilatación sujetando fuertemente los extremos de un cierto material, veríamos que nuestro esfuerzo es en vano, ya que este efecto ocurre con una fuerza violenta.
Al calentar una barra de acero de 5 mm de diámetro, aumentando su temperatura tan sólo un grado Celsius, la barra se dilata en una magnitud tal, que si deseáramos obtener el mismo efecto por esfuerzo mecánico, deberíamos colgar de la barra un peso de 2 600 kg, ¡más de 2,5 toneladas!
El talento humano no sólo ha logrado dominar técnicamente la dilatación cuando es indeseable, sino que ha ido más allá: la ha utilizado para su provecho. Los puentes, cuando son largos, se dividen en segmentos que descansan a su vez sobre bases rodantes para permitir la libre dilatación. Entre los segmentos se dejan espacios para que puedan alargarse sin problemas.
Las construcciones de acero y concreto son posibles únicamente porque el concreto y el acero —¡por casualidad!— tienen el mismo coeficiente de dilatación longitudinal. Los tubos de cobre deben descansar libremente o ser colocados de tal manera que puedan dilatarse.
En cuanto a la pregunta de cuál de los cuerpos se dilata al ser enfriado, se suele responder a la ligera: el hielo, olvidando que el agua posee esta dilatabilidad anómala sólo en estado líquido. El hielo, en cambio, no se dilata al ser enfriado, sino que se contrae, lo mismo que la mayoría de los cuerpos de la naturaleza.
No obstante, existen otros sólidos que se dilatan cuando se enfrían por debajo de cierta temperatura. En primer lugar, son el diamante, el óxido cuproso y la esmeralda. El diamante comienza a dilatarse al ser enfriado considerablemente, a saber, a 42 ºC bajo cero, mientras que el óxido cuproso y la esmeralda presentan la misma particularidad con un frío moderado, de unos 4 ºC bajo cero. Luego a 42 y 4 grados centígrados bajo cero, respectivamente, estos cuerpos tienen la densidad máxima, lo mismo que el agua a +4 ºC.
El yoduro de plata cristalino (el mineral llamado yodirita, yodargirita o yodargira) se dilata al ser enfriado a temperatura ordinaria. Una varilla de goma extendida por una pesa presenta la misma particularidad: se acorta al ser calentada.
Mediante el contacto de la epidermis con un objeto se perciben sensaciones de frío o de calor. Los conceptos de calor y frío son totalmente relativos y sólo se pueden establecer con la relación a un cuerpo de referencia como, por ejemplo, la mano del hombre. Lo que se percibe con más precisión es la temperatura del objeto o, más exactamente todavía, la diferencia entre la temperatura del mismo y la de la mano que la toca.
Ahora bien, aunque la sensación experimentada sea tanto más intensa cuanto más elevada sea la temperatura, se trata sólo una apreciación muy poco exacta que no puede considerarse como medida de temperatura. Para efectuar esta última se utilizan otras propiedades del calor, como la dilatación, cuyos efectos son susceptibles. Temperatura es, entonces, la cantidad de calor que posee un cuerpo.
Con muy pocas excepciones todos los cuerpos aumentan de volumen al calentarse y disminuyen cuando se enfrían. En caso de los sólidos, el volumen suele incrementarse en todas las direcciones.
La dilatación es, por consiguiente, una primera propiedad térmica de los cuerpos, que permite llegar a la noción de la temperatura. La segunda magnitud fundamental es la cantidad de calor que se supone reciben o ceden los cuerpos al calentarse o al enfriarse, respectivamente.