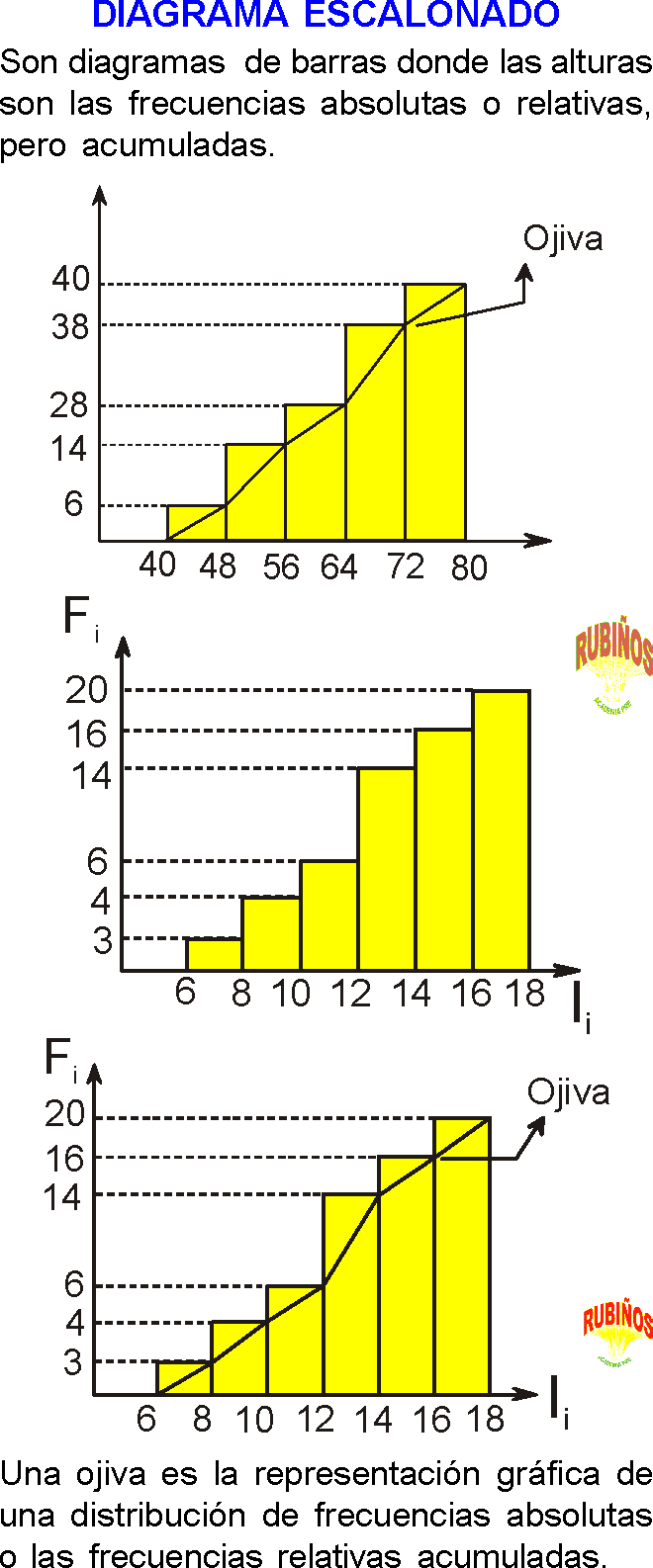
TABLAS DE FRECUENCIAS EJERCICIOS RESUELTOS PDF
EJERCICIO 1 :
La gráfica muestra la ojiva de la frecuencia relativa acumulada de las notas de un examen de estadística. Determine el porcentaje de estudiantes que obtuvieron una nota entre 35 y 72.
A) 58%
B) 52%
C) 56%
D) 50%
E) 54%
RESOLUCIÓN :
Pasando los datos de la gráfica a una tabla, obtenemos
Por lo tanto, el porcentaje de estudiantes que obtuvieron notas entre 35 y 72 es 54%.
Rpta. : "E"
EJERCICIO 2 :
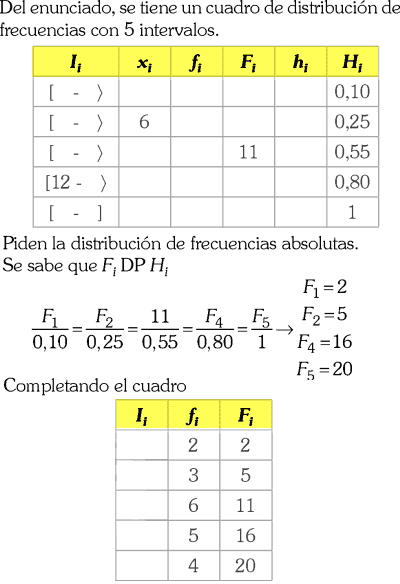
Los tiempos de vida útil (en días) de un tipo de batería se tabuló en una distribución de frecuencias de 5 intervalos de igual amplitud con frecuencias relativas acumuladas: 0,10; 0,25; 0,55; 0,80 y 1,00. Determine la distribución de frecuencias absolutas si la tercera frecuencia absoluta acumulada es 11, si la segunda marca de clase es 6, y si el límite inferior del cuarto intervalo es 12.
A) 1, 4, 6, 4, 5
B) 2, 4, 5, 6, 3
C) 2, 3, 6, 5, 4
D) 4, 2, 5, 6, 3
E) 3, 4, 4, 5, 4
RESOLUCIÓN :
Rpta. : "C"
EJERCICIO 1 :
En el gráfico de ojiva porcentual, se muestran las edades de cierto número de personas. ¿Qué porcentaje de personas tiene edades comprendidas entre 14 y 20 años?
A) 14%
B) 84%
C) 33%
D) 18%
E) 51%
RESOLUCIÓN :
Rpta. : "D"
PRACTICA
PROBLEMA 1 :
Indicar el tamaño de a muestra de la siguiente distribución de datos.
3 4 0 2 5 3
2 7 4 3 1 1
8 6 6 4 5 4
7 5 4 6 0 2
A) 9
B) 20
C) 18
D) 24
E) 36
Rpta. : "D"
PROBLEMA 2 :
Hallar la suma del tamaño de la muestra más la amplitud de siguiente distribución de datos.
2 5 0 5 7 0 4
5 4 1 6 8 5 3
3 2 2 3 9 3 4
8 3 0 2 8 2 3
4 6 4 5 7 1 5
A) 35
B) 9
C) 44
D) 56
E) 39
Rpta. : "C"
PROBLEMA 3 :
Cuál es la suma de las frecuencias absolutas del 5; 7 y 9 de la siguiente tabla de datos.
1 3 9 2 9 2 7 5 3
2 5 1 2 3 7 5 2 3
7 3 5 3 7 2 2 7 2
7 7 4 4 9 1 5 8 9
6 4 7 5 5 9 9 7 5
A) 43
B) 31
C) 27
D) 20
E) 23
PROBLEMA 4 :
La inversión anual, en miles de dólares, de una muestra de 40 pequeñas empresas fueron:
36; 19; 29 ; 37; 33 ; 27; 27; 24 ; 26 ; 31 15 ; 41 ; 30; 18; 39 ; 46 ; 26 ; 12 ; 23 ; 18 33 ; 25 ; 28 ; 23 ; 28 ; 22 ;29 ; 31; 21 ; 35 27 ; 17 ; 31 ; 10 ; 28 ; 20 ; 4 ; 25 ; 34 ; 24
Elabore una distribución de frecuencias con 7 intervalos de clase.
El porcentaje de empresas con una inversión entre entre 14 mil y 20 mil dólares es:
A) 8,5%
B) 11,5%
C) 12,5%
D) 15%
E) 17,5%
Rpta. : "C"
PROBLEMA 5 :
En los resultados de un examen se observó lo siguiente :
☛ 72% de los evaluados tienen a lo más nota 15
☛ 47% de los evaluados tienen una nota menor que 11
☛ La nota mínima aprobatoria es 11
¿Qué porcentaje de los aprobados tiene a lo más el 75% de la nota máxima , siendo está igual a 20?
A) 48
B) 47,17
C) 46
D) 42
E) 41,3
Rpta. : "B"
PROBLEMA 6 :
Indicar verdadero (V) o falso (F) según corresponda:
( ) Cada uno de los elementos de una muestra se llama unidad estadística
( ) Un dato muestral sólo puede pertenecer a uno de los intervalos de clase
( ) Marca de clase es el punto medio de un intervalo de clase
( ) La ojiva es un polígono de frecuencias construido a partir del histograma
A) VVVV
B) VFVF
C) FVFV
D) VVFF
E) FFVV
Rpta. : "D"
PROBLEMA 7 :
Al clasificar las notas de 0 a 100 de un examen, se obtuvo una distribución simétrica con 5 intervalos de clase de igual ancho. Si el 10% de alumnos desaprobó con menos de 20, mientras que los 2/5 del total obtuvieron notas comprendidas entre 40 y 60, ¿qué porcentaje de alumnos obtuvieron una nota menor de 60?
A) 65%
B) 70%
C) 72%
D) 75%
E) 80%
Rpta. : "B"
PROBLEMA 8 :
En una tabla de frecuencias se pudo apreciar que se había tomado 5 intervalos de clase con ancho común. En el segundo intervalo: [60; 80[, había 8 datos. El 20% del total de los datos se encuentra en el tercer intervalo. Las frecuencias relativas del cuarto y quinto intervalo son iguales.
¿Cuántos datos son menores a 120, si 16 son mayores a 80? . Se ha estudiado 40 datos
A) 30
B) 32
C) 34
D) 36
E) 38
Rpta. : "D"
PROBLEMA 9 :
De las proposiciones:
( ) El ancho de un intervalo de clase, depende de la cantidad de datos que contenga
( ) Un pictograma es un gráfico circular dividido en varios sectores
( ) En una misma muestra, la frecuencia relativa es directamente proporcional a la frecuencia absoluta
( ) Al clasificar los datos: 2; 3,5; 4; 2,8; 7; 5,1; se considerará una variable cuantitativa continua ¿cuántas son verdaderas?
A) 0
B) 1
C) 2
D) 3
E) 4
Rpta. : "B"
FRECUENCIA ABSOLUTA
Es el número de observaciones que se registran en cada clase.
La suma total de las frecuencias absolutas es igual al número total de elementos (n).
FRECUENCIA RELATIVA
Es la proporción de observaciones en cada clase.
La suma de todas las frecuencias relativas es igual a la unidad. Se calculan dividiendo cada una de las frecuencias absolutas entre el tamaño de la muestra.
FRECUENCIA ABSOLUTA ACUMULADA
Es la acumulación ordenada de cada una de las frecuencias absolutas.
La última frecuencia absoluta acumulada es igual al número de elementos (n).
Para calcular las frecuencias absolutas acumuladas debemos considerar que la primera frecuencia absoluta acumulada es siempre igual a la primera frecuencia absoluta y a partir de la segunda frecuencia absoluta acumulada, estas se calculan sumando o acumulando las frecuencias absolutas anteriores.
FRECUENCIA RELATIVA ACUMULADA
Es la acumulación de cada frecuencia relativa.
La última frecuencia relativa acumulada es igual a la unidad.
Para calcular las frecuencias relativas acumuladas debemos considerar que la primera frecuencia relativa acumulada es siempre igual a la primera frecuencia relativa y a partir de la segunda frecuencia relativa acumulada, estas se calculan sumando o acumulando las frecuencias relativas anteriores.
Una tabla de distribución de frecuencias es una tabla donde se presentan los datos a analizar con sus respectivas frecuencias relativas y absolutas.
ELEMENTOS DE UNA TABLA DE DISTRIBUCIÓN DE FRECUENCIA
ALCANCE
Es el intervalo cerrado definido por los datos de menor y mayor valor y máximo valor.
RANGO
Es la diferencia entre los datos mayor y menor valor .
INTERVALO DE CLASE
Es una clasificación de los datos en subgrupos, particionar el alcance.
LÍMITES DE CLASE
Son los valores extremos del intervalo de clase.
ANCHO DE CLASE
Es la diferencia entre límite superior e inferior de cada intervalo.
También se le conoce como el tamaño del intervalo de clase.
MARCA DE CLASE
Es el punto medio de cada intervalo.
Es un valor que representa a los datos del intervalo de clase, se calcula como la semisuma de los límites inferior y superior del intervalo de clase.
REGLA DE STURGES
Es para determinar un primer valor aproximado del número de intervalo de clase (K).
K= 1+3,3logn
n: número de datos.
Para garantizar que los valores mayores se encuentren en el último intervalo, el valor de K se redondea al entero siguiente
FRECUENCIA ABSOLUTA
Es el número de observaciones que se registran en cada clase.
La suma total de las frecuencias absolutas es igual al número total de elementos (n).
FRECUENCIA RELATIVA
Es la proporción de observaciones en cada clase.
Nos indica que fracción del total se encuentra en cada intervalo.
Se obtiene como el cociente frecuencia absoluta entre el total de elementos (n).
FRECUENCIA ABSOLUTA ACUMULADA
Es la acumulación ordenada de cada una de la frecuencias absolutas, es decir es la suma de todas las frecuencias absolutas simples desde el primer intervalo de clase hasta el i-énesimo intervalo
FRECUENCIA RELATIVA ACUMULADA
Es la acumulación ordenada de las frecuencias relativas. Indica qué parte del total de datos se encuentran desde el primer intervalo de clase hasta el i-énesimo intervalo.
Se calcula como el cociente de las frecuencias absoluta acumulada y el número de datos.
Para obtener el tanto por ciento basta multiplicar este valor por 100.
EJERCICIO 1 :
Analizar el siguiente enunciado :
Un investigador desea determinar en un colegio en el nivel primaria el número de horas semanales que los niños de 7 años de edad se dedican a ver programas de televisión.
Una muestra de 25 niños arrojó los siguientes resultados (en número de horas semanales):
10; 19; 25; 19; 26; 16; 19; 27; 27; 25; 23; 22; 17; 12; 20; 15; 21; 23; 26; 14; 18; 25; 23; 24; 21.
RANGO
r=27–10=17
INTERVALO DE CLASE
[16;19> es un posible intervalo de clase donde se debe considerar a los niños que se dedican a ver televisión desde 16 horas hasta menos de 19 horas semanales.
LÍMITES DE CLASE
en el intervalo [16;19> se observa que 16 es el límite inferior y 19 es el límite superior.
ANCHO DE CLASE
en el intervalo [16;19> se observa que el ancho de clase es W = 19 – 16 = 3
MARCA DE CLASE
en el intervalo [16 ; 19> la marca de clase es : (16+19 )/2 = 17,5
