MOVIMIENTO ARMÓNICO SIMPLE EJERCICIOS RESUELTOS PDF M.A.S. OSCILACIONES
APRENDIZAJES ESPERADOS
☛ Estudiar los movimientos periódicos, oscilatorios , para describir y analizar adecuadamente el M.A.S.
☛ Conocer las características cinemáticas , dinámicas y energéticas en un M.A.S. y representarlas matemáticamente.
¿QUÉ ES EL MOVIMIENTO ARMÓNICO SIMPLE?
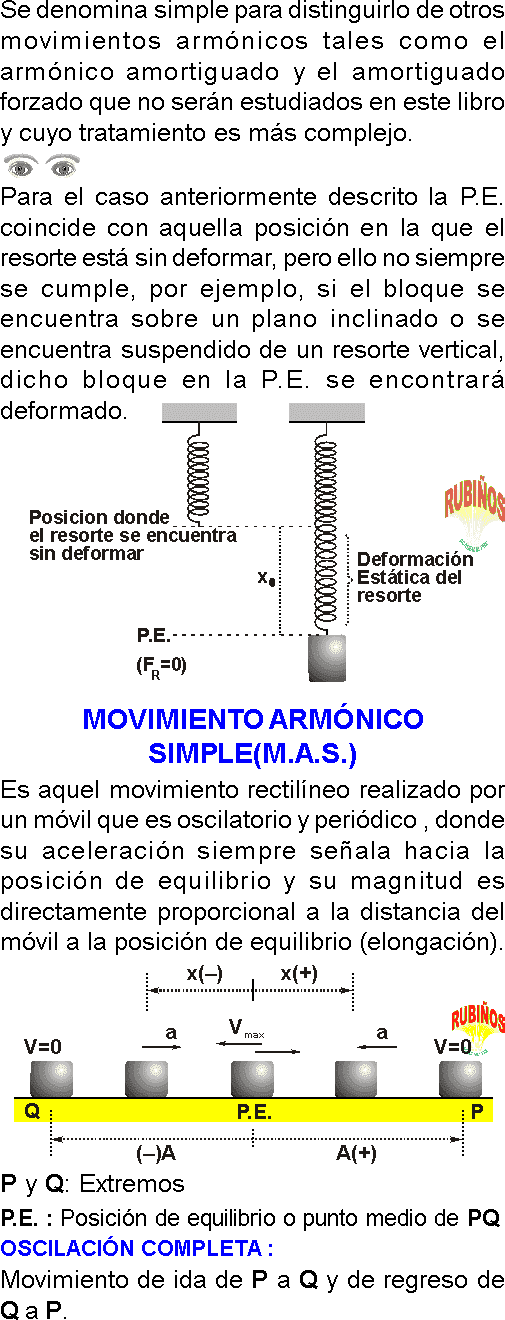
El movimiento armónico simple es aquel movimiento rectilíneo realizado por un móvil que es oscilatorio y periódico , donde su aceleración siempre señala hacia la posición de equilibrio y su magnitud es directamente proporcional a la distancia del móvil a la posición de equilibrio (elongación).
El M.A.S. es aquel movimiento rectilíneo, oscilatorio y periódico que está gobernado por una fuerza llamada fuerza recuperadora.
El MAS es producido la fuerza recuperadora elástica: F=– kx, donde k es la constante elástica. En este tipo de movimiento se prescinde de la fricción.
ELEMENTOS DEL MAS
OSCILACIÓN O VIBRACIÓN
Es un movimiento de ida y vuelta que se produce cuando un sistema se aleja de la posición de equilibrio
PERIODO (T)
Es el intervalo de tiempo que tarda cualquier punto del sistema en realizar una oscilación.
FRECUENCIA (F)
Es el número de oscilaciones realizadas en un intervalo de tiempo.
ELONGACIÓN (x)
Es el desplazamiento de cualquier punto del sistema respecto a la posición de equilibrio.
Por ejemplo, el desplazamiento x del centro de masa del bloque respecto a la posición x=0
AMPLITUD (A)
Es la máxima elongación.
Por ejemplo, el máximo desplazamiento del centro de masa del bloque desde x=0 hasta x=± A
ACELERACIÓN DE UN OSCILADOR CON MAS
De la segunda ley de Newton se deduce que la aceleración es directamente proporcional a la posición
PERIODO DE OSCILACIÓN DE UN SISTEMA BLOQUE – RESORTE
Indica el intervalo de tiempo que tarda cualquier punto del sistema en realizar una oscilación.
RELACIÓN ENTRE EL MAS Y EL MCU
El M.A.S de una partícula se puede considerar como la proyección del MCU de la partícula sobre cada uno de los ejes de un sistema de coordenadas.
Entonces el MCU de la partícula se puede descomponer en dos MAS independientes a lo largo de los ejes coordenados x e y cuya amplitud de oscilación es A=R
PRIMERA PRACTICA
EJERCICIO 1 :
Un bloque se encuentra sostenido de un resorte, cuya constante elástica es K=20N/m y realiza un M.A.S además la masa del bloque es 200g . Calcula el período.
A) 𝛑/5s
B) 𝛑/2s
C) 1s
D) 𝛑s
E) 10𝛑s
Rpta. : "A"
EJERCICIO 2 :
Según la ecuación del M.A.S. x(t)=4sen(2𝛑t + 0,5𝛑)m; calcula la posición del móvil para t=0s
A) 0m
B) 2m
C) 4m
D) –4m
E) –2m
Rpta. : "C"
EJERCICIO 3 :
Con los datos de la pregunta anterior .Calcula el período de movimiento del M.A.S.
A) 1s
B) 2s
C) 0,1s
D) 4s
E) 3s
Rpta. : "A"
EJERCICIO 4 :
Un bloque de 20kg cuelga de un resorte de k=2000N/m. Si el sistema se encuentra en equilibrio Calcula la deformación que experimenta el resorte.
A) 10m
B) 1m
C) 10cm
D) 0,1cm
E) 0,01m
Rpta. : "C"
EJERCICIO 5 :
Si en un instante se corta la cuerda que sostiene al bloque del problema anterior. Calcula el período si realiza un M.A.S
A) 𝛑s
B) 0,5𝛑s
C) 0,4𝛑s
D) 0,2𝛑s
E) 5𝛑s
Rpta. : "D"
EJERCICIO 6 :
Para un bloque de 0,2kg que realiza un M.A.S. sujeto a un resorte de constante K = 20N/m. Si su amplitud es 2m. Calcula su velocidad máxima.
A) 20m/s
B) 10m/s
C) 15m/s
D) 2m/s
E) 5m/s
Rpta. : "A"
EJERCICIO 7 :
Con los datos del ejercicio anterior . Calcula su aceleración máxima.
A) 20m/s²
B) 100m/s²
C) 150m/s²
D) 200m/s²
E) 40m/s²
Rpta. : "D"
EJERCICIO 8 :
Calcula el período de un bloque que realiza un M.A.S. si se sabe que realiza 80 oscilaciones simples en 160s.
A) 2s
B) 4s
C) 3s
D) 1s
E) 5s
Rpta. : "B"
EJERCICIO 9 :
Si un bloque realiza un M.A.S. Calcula su energía potencial elástica máxima si se sabe que cuándo su aceleración es máxima su deformación es 2m. k=25N/m
A) 10J
B) 20J
C) 50J
D) 100J
E) 200J
Rpta. : "C"
EJERCICIO 10 :
Si una partícula atada a una cuerda de longitud L realiza un M.A.S. de período “T”. Si la misma partícula es llevada a otro planeta donde la gravedad es 3 veces la gravedad de la Tierra. En cuanto se debe aumentar o disminuir la longitud de la cuerda L para que el período no cambié.
A) Disminuir en L/2
B) Aumentar en 2L
C) Aumentar en 3L
D) Disminuir en 2L
E) Aumentar en L
Rpta. : "B"
EJERCICIO 11 :
Halla el periodo de un M.A.S. si se sabe que la relación entre la máxima aceleración y su máxima velocidad es 4𝛑
A) 0,5s
B) 0,2s
C) 0.,4s
D) 0,1s
E) 0,8s
Rpta. : "A"
EJERCICIO 12 :
Un cuerpo de 2kg está suspendido de un resorte. Si se aplica una fuerza adicional de 10 Newton el resorte se alarga 5cm. ¿Cuál es el periodo de oscilación si se le suelta?
A) 𝛑/2
B) 𝛑/3
C) 𝛑/10
D) 𝛑/4
E) 𝛑/5
Rpta. : "E"
EJERCICIO 13 :
Una masa de 5kg está animada de un M.A.S., en el que se realiza 3 oscilaciones por segundo. Calcula el valor de la fuerza recuperadora para una elongación de 5cm.
A) 56,4N
B) 48,2N
C) 88,7N
D) 62,8N
E) 74,5N
Rpta. : "C"
EJERCICIO 14 :
Un sistema oscila armónicamente con una frecuencia de 10Hz y una amplitud de 4m. Determina la ecuación del movimiento con respecto a su posición en cualquier instante “t” segundos. Considera una constante de fase 30°.
A) x=4Sen(20𝛑t + 𝛑/6)
B) x=4Sen(10𝛑t + 𝛑/6)
C) x=4Sen(20𝛑t + 𝛑/3)
D) x=2Sen(10𝛑t + 𝛑/6)
E) x=2Sen(20𝛑t + 𝛑/3)
Rpta. : "A"
EJERCICIO 15 :
Un bloque de 200g de masa cuelga de un resorte ligero cuya constante de fuerza es 20N/m. El bloque es jalado hacia abajo 10cm a partir de su posición de equilibrio. El tiempo, en segundos que tarda en pasar por el punto de equilibrio por primera vez luego de ser soltado es:
A) 0,005𝛑
B) 0,02𝛑
C) 0,05𝛑
D) 1,65𝛑
E) 6,6𝛑
Rpta. : "C"
EJERCICIO 16 :
Al suspender un bloque de un resorte, la longitud de este se alarga en 10cm. Halla el periodo de oscilación cuando se tira del cuerpo hacia abajo y se abandonó luego así mismo (en s).
(g=10m/s²)
A) 𝛑/2
B) 𝛑/3
C) 𝛑/10
D) 𝛑/4
E) 𝛑/5
Rpta. : "E"
EJERCICIO 17 :
Si la ecuación x=0,40Cos(2t + 0,25𝛑)m representa la elongación de un oscilador armónico de 5kg de masa. Halla la energía total del sistema en cualquier instante (en J)
A) 1,2
B) 1,6
C) 1,8
D) 1,5
E) 2,2
Rpta. : "B"
EJERCICIO 18 :
Un cuerpo de masa “m” cuelga del extremo de un resorte realizando un movimiento armónico simple del periodo T. Determina el valor de la masa que se deba colocar en el extremo de este resorte (en lugar de la masa anterior) para que el periodo del movimiento sea 3T.
A) 9m
B) 6m
C) 3m
D) m/3
E) m/9
Rpta. : "A"
EJERCICIO 19 :
El periodo de oscilación de un péndulo simple es √10 s , si su longitud disminuye en un 10%. Determina su nuevo periodo.
A) 1s
B) 2s
C) 3s
D) 4s
E) 6s
Rpta. : "C"
EJERCICIO 20 :
Halla el periodo de oscilación de un péndulo simple, el cual se encuentra a una altura sobre la superficie terrestre, igual a la mitad del radio de la Tierra.
(longitud=1m y 𝛑²=9,8)
A) 1s
B) 3s
C) 2s
D) 4s
E) 5s
Rpta. : "B"
EJERCICIO 21 :
Un sistema masa resorte ejecuta un M.A.S., con un periodo de 4s. Halla la aceleración máxima. Si la velocidad máxima es de 2m/s (en m/s²)
A) 2
B) 𝛑
C) 𝛑/2
D) 2/𝛑
E) 2𝛑
Rpta. : "B"
PROBLEMAS RESUELTOS
PROBLEMA 1 :
El tiempo mínimo que demora una partícula que realiza un MAS, para alcanzar la amplitud máxima desde la posición de equilibrio, es de 1,5 s. Si la magnitud de la aceleración máxima es de 4cm/s² calcule en cm/s, la rapidez máxima.
A) 12/𝛑
B) 4/𝛑
C) 6/𝛑
D) 8/𝛑
E) 15/𝛑
RESOLUCIÓN :
Rpta. : "A"
PROBLEMA 2 :
Un bloque de masa m realiza un MAS. Calcule qué porcentaje de la rapidez máxima tiene el bloque cuando su elongación es el 28% de su amplitud máxima.
A) 28
B) 42
C) 50
D) 75
E) 96
RESOLUCIÓN :
Rpta. : "E"
PROBLEMA 3 :
El extremo de un rosorte está sujeto a una pared y el otro está unido a un bloque de masa de 2 kg que oscila sobre uno superficie lisa. Halle la amplitud (en m) de oscilación del bloque, si su rapidez en la posición de equilibrio es l0 m/s. La constante de elasticidad del resorte es 300 N/m. g= 9,81 m/s²
A) √(2/3)
B) 2/3
C) 1
D) √(3/2)
E) 3/2
RESOLUCIÓN :
Rpta. : "A"
PROBLEMA 4 :
La velocidad máxima que adquiere una masa con movimiento armónico simple es 2m/s y su amplitud es 5×10–2 m. Si el sistema duplica su amplitud manteniendo su frecuencia, la aceleración máxima en m/s², que adquiere bajo esta condición es
A) 20
B) 40
C) 80
D) 160
E) 320
RESOLUCIÓN :
Rpta. : "D"
SEGUNDA PRACTICA
PROBLEMA 1 :
Un resorte helicoidal, horizontal, se estira 0,076 m con respecto a su posición de equilibrio cuando actúa sobre él una fuerza de 3,34 N. Se toma un cuerpo de 0,68 kg, se fija al extremo del resorte y se tira 10 cm a partir de su posición de equilibrio.
Al soltar el cuerpo se ejecuta un M.A.S., determinar:
A) ¿Cuál es la constante de rigidez del resorte?
B) ¿Cuál es la fuerza que ejerce el resorte sobre el cuerpo de 0,68 kg cuando está a punto de ser soltado?
C) ¿Cuál es el período de oscilación después de soltar el cuerpo?
D) ¿Cuál es la amplitud del movimiento?
E) ¿Cuál es la máxima velocidad del cuerpo en vibración?
F) ¿Cuál es la máxima aceleración del cuerpo?
G) La velocidad, aceleración, energías cinética y potencial del cuerpo cuando se ha movido a la mitad de su distancia hacia el centro del movimiento a partir de su posición inicial?
PROBLEMA 2 :
Un cubo de 0,5 kg conectado a un resorte ligero para la cual la constante de fuerza es 20 N/m, oscila sobre una pista horizontal sin fricción.
Determinar:
I) La energía total del sistema y la rapidez máxima del cubo si la amplitud del movimiento es de 0,03 m.
II) La velocidad cuando el desplazamiento es igual a 0,02 m.
III) Las energías cinética y potencial del sistema cuando x=0,02
PROBLEMA 3 :
Una partícula de masa m=200g oscila sobre una superficie horizontal lisa, unida a un resorte con una amplitud de 80cm cuando su estiramiento es 62,1cm en la dirección +x, su velocidad es 5m/s.
¿Cuál es el valor de la constante del resorte?
A) 5
B) 20
C) 2
D) 10
E) 5
Rpta. : "B"
PROBLEMA 4 :
Una partícula de masa m=0,32kg está oscilando en el extremo de un resorte, con 0,25 m de amplitud se encuentra en su posición de equilibrio (x=0), moviéndose en dirección de +x, cuando t = 0 y 0,12 s después está en x=0,2 m. Calcule la constante del resorte (en N/m).
A) 1,89
B) 36,2
C) 18,9
D) 3,62
E) 200
Rpta. : "C"
PROBLEMA 5 :
Un cuerpo realiza un movimiento armónico simple sujeto al extremo de un resorte. Diga en cuál de los siguientes casos la frecuencia del movimiento aumenta:
A) El cuerpo es sustituido por otro de menor masa.
B) El cuerpo oscila con mayor amplitud.
C) El cuerpo oscila con menor amplitud.
D) El cuerpo es sustituido por otro de mayor peso.
E) El resorte es sustituido por otro con constante de resorte menor.
Rpta. : "A"
PROBLEMA 6 :
¿Cuántas de las siguientes proposiciones son verdaderas?
1) La frecuencia de oscilación depende de la amplitud.
2) La frecuencia de un sistema masa-resorte que oscila horizontalmente, es diferente a la frecuencia del mismo sistema que oscila verticalmente.
3) La frecuencia de oscilación depende de la constante k del resorte.
4) Para un mismo sistema masa-resorte las oscilaciones verticales y horizontales tienen la misma frecuencia.
5) Un sistema masa-resorte que realiza un M.A.S., se lleva a un planeta de mayor aceleración de la gravedad que en la tierra. En este planeta la frecuencia del M.A.S. se incrementa.
6) Las oscilaciones en el M.A.S. se consideran respecto al estado no deformado del resorte.
7) En todo M.A.S. la energía se conserva.
8) La energía potencial y cinética, en función de la posición, en un M.A.S. son funciones cuadráticas.
9) Los valores máximos de la energía potencial y cinética en un M.A.S. son iguales a la energía total.
A) 1
B) 9
C) 6
D) 7
E) 5
Rpta. : "E"
PROBLEMA 7 :
Un cuerpo de masa m unido a un resorte de constante k se mueve con amplitud A en un plano horizontal.
¿Cuál de las siguientes afirmaciones es falsa?
A) La energía del sistema masa-resorte no depende de la masa m del cuerpo.
B) La energía cinética es máxima en los extremos del movimiento.
C) La aceleración es máxima en los extremos de su trayectoria.
D) La energía potencial es mínima en la posición de equilibrio.
E) El período de oscilación es proporcional a √m
Rpta. : "B"
PROBLEMA 8 :
Una masa de 1 kg fija al extremo de un resorte de constante k = 49 N/m se mueve con M.A.S. con una amplitud de 12 cm, al respecto señale la veracidad (V) o falsedad (F) de las siguientes proposiciones:
I) La energía total del sistema es 0,70J
II) Su energía cinética cuando x=6cm es 3/4 de la energía mecánica total.
III) Su rapidez máxima es 0,84 m/s
A) FVV
B) FFF
C) VVV
D) FFV
E) VVF
Rpta. : "A"
PROBLEMA 9 :
Dos resortes, R1 de alargamiento 2mm/N y R2 de 5mm/N, tienen la misma longitud sin carga. Son colgados del mismo soporte en la parte superior y son ligados solidarios en la parte inferior. Al colocar una pesa de 5N, el sistema se va a estirar:
A) 25/7mm
B) 50/7mm
C) 75/7mm
D) 5/7mm
E) 7/5mm
Rpta. : "B"
PROBLEMA 10 :
Un cuerpo cuelga del extremo de un resorte y oscila verticalmente con el período de 2 s. Al aumentar la masa del cuerpo en 1 kg, el nuevo período es de 4s.
¿Cuál es el valor de la masa inicial?
A) 1/2 kg
B) 1/3 kg
C) 1/4 kg
D) 1/6 kg
E) 1 kg
Rpta. : "B"
PROBLEMA 11 :
Una masa de 0,2 kg fija al extremo de un resorte de constante k=1N/m se suelta partiendo del reposo, cuando t=0s desde una posición de estiramiento máximo. Después de 0,5s se mide la velocidad y resulta –1,5 m/s. Determine la energía total del sistema en joule.
A) 0,17
B) 0,27
C) 0,47
D) 0,32
E) 0,57
Rpta. : "B"
En la naturaleza encontramos diversas formas de movimiento mecánico, pero una de las que se encuentra ampliamente difundida en nuestro entorno es el movimiento vibratorio u oscilatorio. Un ejemplo directo de este tipo de movimiento puede ser el vaivén de un péndulo; o el vaivén de las ramas de un árbol por acción del viento; etc.
Por supuesto que el alumno está familiarizado con otros ejemplos más de oscilaciones mecánicas: las vibraciones de las cuerdas de una guitarra; de nuestras cuerdas vocales, cuando hablamos.
También se conoce otro tipo de oscilaciones, en las ondas electromagnéticas los vectores del campo eléctrico y magnético oscilan, en los circuitos eléctricos se pueden tener voltajes y corrientes oscilantes, etc.
A pesar de que mencionamos diferentes tipos de oscilaciones mecánicas e incluso oscilaciones de otra naturaleza; el aparato matemático que las describe es el mismo.
Casi todo el contenido de este capítulo está dedicado al M.A.S (Movimiento Armónico Simple) y al movimiento pendular, sin embargo, las leyes físicas que se deduzcan se podrán utilizar en la acústica, física molecular, óptica y mecánica cuántica.
Conocer el movimiento oscilatorio y sus elementos es un requisito indispensable para hacer una buena descripción de las ondas de diversa índole: mecánica o electromagnética.
ALGUNAS APLICACIONES Y USOS DEL MOVIMIENTO OSCILATORIO
☛ La oscilación forzada del pistón sobre el cilindro del motor de automóvil.
☛ Las oscilaciones de los electrones en los cables conductores derivados a un osciloscopio se muestran la razón de denominarse corriente alterna
☛ Las oscilaciones de las partículas de un sólido que ha sido golpeado
☛ En medicina la respuesta de nuestro corazón o cabeza a ciertos estímulos eléctricos; registran señales vibratorias en una pantalla, placa o papel (electrocardiogramas, electroencefalogramas) que sirven para realizar análisis y diagnóstico clínico.
Existen otras aplicaciones en radio, TV, telefonía celular, etc; pero empecemos en este capítulo de la mecánica con el estudio de las oscilaciones.
Se dice que un punto sigue un movimiento armónico simple cuando su posición en función del tiempo es una sinusoide. Es un movimiento periódico de vaivén; en el que un cuerpo oscila a un lado y a otro de su posición de equilibrio en una dirección determinada y en intervalos iguales de tiempo.
Una partícula sometida a este tipo de movimiento tendrá un punto central (punto de equilibrio), alrededor del cual oscilará.
Un ejemplo de M.A.S. se da cuando apartamos una masa “m”, unida a un muelle, de su punto de equilibrio y luego se suelta, el muelle provoca en la masa “m” oscilaciones periódicas, tal movimiento, despreciando las fricciones, es uno de los tantos ejemplos de Movimiento Armónico Simple (M.A.S.).