ANÁLISIS VECTORIAL EJERCICIOS RESUELTOS DE INGRESO UNIVERSIDAD – OPERACIONES CON VECTORES
¿Qué es un vector en física?
Un vector es una herramienta matemática que permite representar una serie de magnitudes físicas, tales como la velocidad, la fuerza, la aceleración, el impulso, etc.
OBJETIVOS DEL APRENDIZAJE
Al finalizar la unidad, el alumno será capaz de :
☛ Definir un vector en el ámbito de la Física.
☛ Identificar los elementos del vector y su relación con las magnitudes físicas vectoriales.
☛ Realizar operaciones con vectores mediante diversos métodos: método del polígono, método del paralelogramo.
☛ Emplear la descomposición rectangular como método alternativo de resolución de problemas.
☛ Conocer el vector unitario
☛ Operar con vectores empleando los vectores unitarios.
En el análisis de los fenómenos físicos, para una mejor comprensión empleamos una serie de magnitudes físicas, muchas de ellas requieren de una dirección, por ejemplo: la aceleración del cohete, el desplazamiento de la persona, la fuerza sobre un cuerpo, la velocidad, el impulso etc.
¿Cómo representamos estas magnitudes físicas que necesitan de una dirección?
Mediante un vector
REPRESENTACIÓN GEOMÉTRICA DE UN VECTOR
Se representa mediante un segmento de recta orientado (flecha).
MÓDULO O MAGNITUD
Es el valor numérico del vector; geométricamente representa el tamaño del vector.
DIRECCIÓN
Ángulo medido en sentido antihorario que inicia en el eje X
OPERACIÓN CON VECTORES
SUMA DE VECTORES
Es un procedimiento mediante el cual, dados dos o más vectores, se obtiene un solo vector denominado vector SUMA o vector RESULTANTE vectores que se suman.
MÉTODO DEL PARALELOGRAMO PARA SUMAR DOS VECTORES.
Para sumar dos vectores que tienen el mismo origen, se construye un paralelogramo, trazando por el extremo de cada vector una paralela al otro.
El módulo del vector suma o resultante se obtiene trazando la diagonal del paralelogramo desde el origen de los vectores.
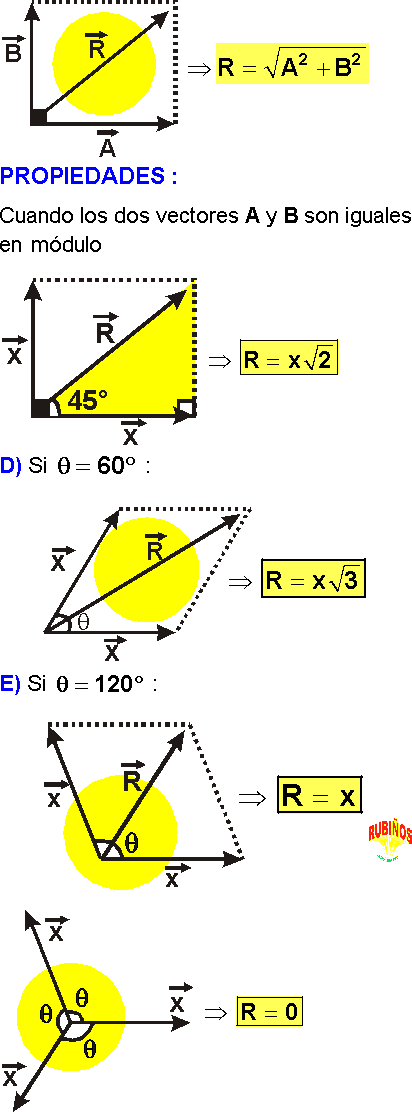
CASOS PARTICULARES
RESULTANTE MÁXIMA
La resultante de dos vectores es máxima, cuando forman entre sí un ángulo de cero grados.
RESULTANTE MÍNIMA
La resultante de dos vectores es mínima, cuando forman entre sí un ángulo de 180°.
RESULTANTE DE DOS VECTORES PERPENDICULARES
Cuando dos vectores forman entre sí un ángulo recto, la resultante se obtiene aplicando el teorema de Pitágoras.
DIFERENCIA DE DOS VECTORES
La diferencia de dos vectores que tienen el mismo origen se consigue uniendo los extremos de los vectores.
El módulo del vector diferencia se determina aplicando la ley de Cosenos
MÉTODO DEL POLÍGONO PARA SUMAR “n” VECTORES
Consiste en construir un polígono con los vectores sumandos, manteniendo constante sus tres elementos (módulo, dirección y sentido), uniendo el extremo del primer vector con el origen del segundo vector, el extremo del segundo vector y el origen del tercer vector, así sucesivamente hasta el último vector.
El módulo del vector resultante se determina uniendo el origen del primer vector con el extremo del último vector.
CASO ESPECIAL (POLÍGONO CERRADO)
Si el polígono de vectores es ordenado (horario o antihorario) y cerrado, entonces la resultante es cero.
DESCOMPOSICIÓN RECTANGULAR
Consiste en escribir un vector en función de dos componentes que forman entre sí un ángulo recto.
𝑖) Si la resultante de un sistema de vectores es VERTICAL, entonces la componente HORIZONTAL es nula.
𝑖𝑖) Si la resultante de un sistema de vectores es HORIZONTAL, entonces la componente VERTICAL es nula.
VECTOR UNITARIO
El vector unitario es aquel cuyo módulo es la unidad y tiene por misión indicar la dirección de un determinado vector.
VECTORES UNITARIOS EN EL PLANO CARTESIANO
A los ejes de coordenadas X e Y, se asocia vectores unitarios característicos
EJERCICIO 1 :
La resultante máxima de dos vectores es 18 y la suma mínima de los mismos es 6. Calcula el módulo de la resultante cuando forman los vectores 90°.
Rpta. : "6√5"
EJERCICIO 2 :
Si la suma máxima de dos vectores es 28 y el cociente de sus módulos es 4/3. Calcula el módulo del mayor.
Rpta. : "16"
EJERCICIO 3 :
La resultante máxima de dos vectores es 14 y la suma mínima de los mismos es 2, calcula la resultante cuando formen 90º los vectores.
Rpta. : "10"
EJERCICIO 4 :
Si la suma máxima de dos vectores es 31u y la suma mínima es 17u. calcula el módulo de la resultante cuando forman 90° los vectores.
Rpta. : "25"
EJERCICIO 5 :
La corriente de un río tiene una velocidad de 12m/s. Si un alumno cruza perpendicularmente un río con una velocidad de 5m/s. ¿Cuál será el valor de la velocidad resultante?
A) 17m/s
B) 7
C) 15
D) 13
E) 12
Rpta. : "D"
EJERCICIO 6 :
Un paracaidista salta y cae verticalmente por acción de su peso igual a 600N. Al abrir el paracaídas el aire ejerce una fuerza sobre el paracaídas de 1000N en dirección vertical y hacia arriba. ¿Cuál es el valor de la fuerza resultante sobre el paracaidista en dicho instante?
A) 1600N
B) 1400
C) 400
D) 600
E) 800
Rpta. : "C"
EJERCICIO 7 :
Dos vectores tienen una resultante mínima que vale 4 y una resultante máxima igual a 16. ¿Cuál es la resultante de estos vectores cuando formen 60°?
A) 7
B) 9
C) 14
D) 5
E) 12
Rpta. : "C"
EJERCICIO 8 :
Un bote a motor se dirige hacia el este con una velocidad de 10m/s. Si la corriente marina mantiene una velocidad de 6m/s, en la dirección N30°E. ¿Cuál será el valor de la velocidad resultante del bote?
A) 16m/s
B) 15
C) 14
D) 12
E) 11
Rpta. : "C"
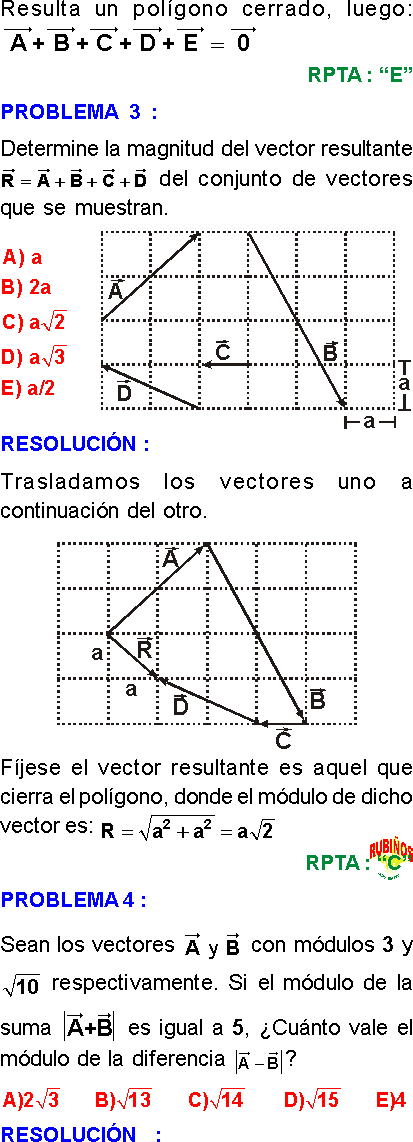
En cada caso, halla el valor y la dirección de los dos componentes de los vectores mostrados.