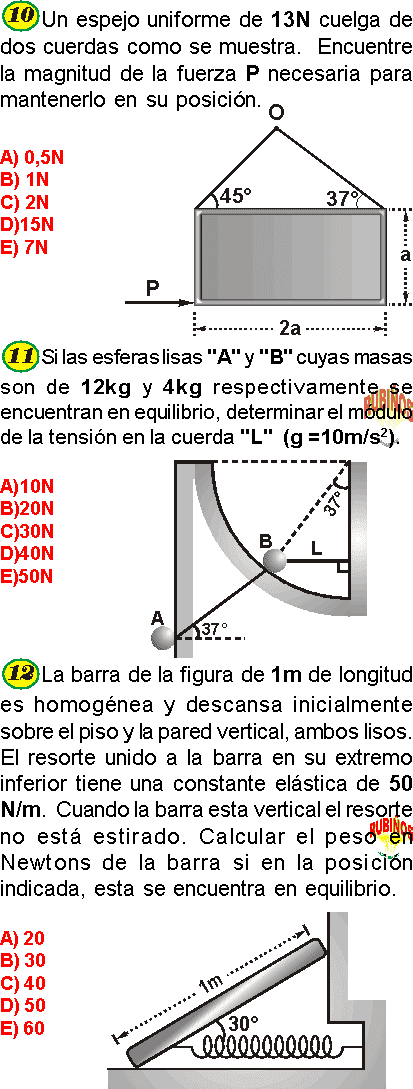
MOMENTO DE FUERZA EJERCICIOS RESUELTOS PDF
APRENDIZAJES ESPERADOS :
☛ Reconocer y determinar la magnitud física denominada momento de una fuerza o torque.
☛ Determinar el momento resultante sobre un cuerpo y sus efectos.
☛ Conocer y aplicar la segunda condición del equilibrio.
En nuestra vida cotidiana los efectos de rotación son muy comunes. Desde el funcionamiento de algunas partes de nuestro propio cuerpo, hasta un gran número de máquinas y herramientas.
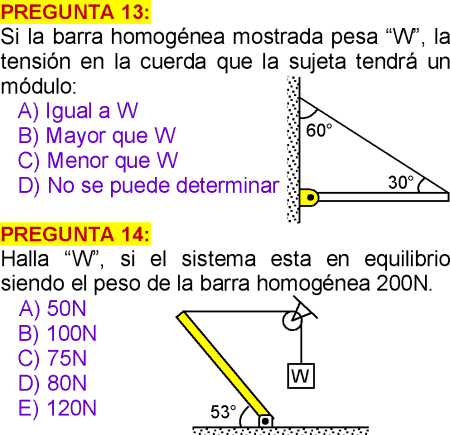
PREGUNTA 1
En la figura, la fuerza del hombre se aplica perpendicularmente al mango del martillo. Si el clavo dista 4 cm del punto de apoyo, ¿cuál es la fuerza que se ejerce sobre él?
A) 8 N
B) 39 N
C) 52 N
D) 26 N
E) 13 N
Resolución
Rpta. : "C"
PREGUNTA 2
En la figura se muestra un sistema en equilibrio. La barra de longitud L tiene un peso de magnitud P y el bloque que cuelga a 3L/4 de la articulación A, tiene un peso de magnitud P/2 . Calcule en N, la magnitud de la fuerza que actúa sobre la barra en el punto A.
A) P√43/2
B) P√43/3
C) P√43/5
D) P√43/4
E) P√43/6
Resolución
Rpta. : "D"
PREGUNTA 3
En el sistema físico en equilibrio de la figura, se calcula que la tensión en la cuerda AC es: (considerar la barra homogénea AB ingrávida).
A) 1,0 kgf
B) 10,0 kgf
C) 12,5 kgf
D) 22,5 kgf
E) 25,0 kgf
Resolución
Rpta. : "C"
¿Qué es el momento de una fuerza ?
Es aquella magnitud física vectorial que mide el efecto o posible efecto de rotación de una fuerza sobre un cuerpo en torno a un punto llamado centro de rotación o centro de momentos.
La unidad del momento de una fuerza es: newton-metro (N·m)
Si la línea de acción de la fuerza pasa por el centro de rotación, esta fuerza no produce efectos de rotación.
Entonces, para que se produzca efectos de rotación la línea de acción de la fuerza no debe pasar por el centro de rotación.
El momento de fuerza se evalúa como:
MoF=F.d
Donde:
MoF: módulo del momento de la fuerza “F” respecto de “O”
O : centro de momentos o rotación.
F : módulo de la fuerza aplicada (en “N”)
d : brazo de la fuerza (en “m”), es la distancia del centro de rotación a la línea de acción de la fuerza.
El MOMENTO DE UNA FUERZA , es una magnitud vectorial; por tanto, se representa con un vector perpendicular al plano de rotación.
Para ello se emplea la regla de la mano derecha.
Por convención se emplea:
☛ Si el efecto de rotación es en sentido antihorario el momento será positivo (+).
☛ Si el efecto de rotación es en sentido horario el momento será negativo (–).
Toda fuerza cuya línea de acción pasa por el centro de rotación, no produce efecto de rotación, su momento es nulo.
MOMENTO RESULTANTE
El momento resultante es la suma de todos los momentos producidos por cada una de las fuerzas que actúan sobre un cuerpo, considerando su respectivo efecto de rotación.
El momento resultante, físicamente nos expresa la medida del efecto neto de rotación que experimenta un cuerpo. Es decir, nos indica hacia donde esta rotando el cuerpo o sistema.
¿Qué es la segunda condición de equilibrio?
Un cuerpo se encuentra en equilibrio de rotación si y solo si el momento resultante sobre él con respecto a cualquier punto es nulo .
Al emplear la segunda condición de equilibrio, el centro de rotación se elije de manera arbitraria y convenientemente en cada problema.
EQUILIBRIO MECÁNICO
un cuerpo se encontrará en equilibrio mecánico, si y sólo sí, sobre el cuerpo o sistema se cumple simultáneamente el equilibrio de traslación y el equilibrio de rotación
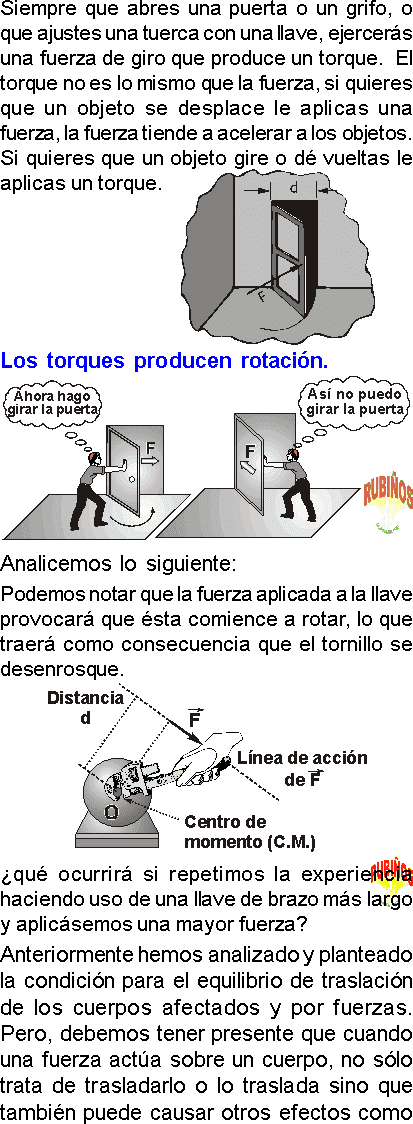
Siempre que abres una puerta o un grifo, o que ajustes una tuerca con una llave, ejercerás una fuerza de giro que produce un torque.
El torque no es lo mismo que la fuerza, si quieres que un objeto se desplace le aplicas una fuerza, la fuerza tiende a acelerar a los objetos.
Si quieres que un objeto gire o dé vueltas le aplicas un torque.
OBSERVACIONES IMPORTANTES :
Para resolver problemas aplicando la segunda condición de equilibrio, se debe tomar en cuenta lo siguiente:
☛ Hacer el D.C.L.
☛ Ubique el punto de giro (O) y desde este punto halle la distancia a cada fuerza que no pasa por este punto.
☛ Iguale los momentos horarios a los antihorarios para garantizar que la suma de momentos sea cero.
☛ Cuando se dice que un cuerpo está en equilibrio se puede usar la primera y/o segunda condición de equilibrio.
☛ Cuando el cuerpo es pequeño (partícula, pesa, bloque, cajón) se emplea solamente la primera condición .
☛ Si el cuerpo es grande (barra, palanca, escalera, viga, ...) en primer lugar se usa la segunda condición de equilibrio y si fuera necesario se usará posteriormente la primera condición .
☛ El momento en forma general, se calcula, ya sea prolongando la línea de acción de la fuerza, o descomponiendo la fuerza.
LOS TORQUES PRODUCEN ROTACIÓN
Anteriormente hemos analizado y planteado la condición para el equilibrio de traslación de los cuerpos afectados y por fuerzas.
Pero, debemos tener presente que cuando una fuerza actúa sobre un cuerpo, no sólo trata de trasladarlo o lo traslada sino que también puede causar otros efectos como deformación y rotación.
El efecto de traslación y deformación de un cuerpo debido a una fuerza ya ha sido estudiado anteriormente, en esta parte analizaremos el efecto de rotación causada por dicha fuerza y las condiciones para el equilibrio de rotación.
Cuando una fuerza actúa sobre un cuerpo, ésta puede o no causar giro, respecto de un punto o eje, esto depende de cómo y dónde actúe la fuerza.
Para caracterizar el efecto de giro producido por una fuerza, sobre un cuerpo, respecto de un punto o eje, utilizamos una magnitud vectorial llamada momento de una fuerza
MOMENTO DE FUERZA O TORQUE
Es una magnitud vectorial, donde su módulo indica el grado de giro que produce una fuerza a un cuerpo alrededor de un punto denominado: centro de momentos o centro de giro.
La dirección del vector momento es perpendicular al plano formado por el centro de giro y la línea de acción de la fuerza y su sentido se determina mediante la regla de la mano derecha.
La dirección de un momento está en el eje de rotación y se determina por la regla de la mano derecha.
CONVENCIÓN DE SIGNOS
Si el cuerpo gira o intenta girar en sentido horario, debido a una fuerza "F", se dice que el momento producido por dicha fuerza es negativo. Si el cuerpo o sistema gira o intenta girar en sentido antihorario.
Debido a una fuerza "F", se dice que el momento producido por dicha fuerza es: positivo.
CASO PARTICULAR :
Cuando una fuerza actúa directamente en el centro de momentos o su línea de acción pasa por dicho punto, el momento producido por la fuerza es cero.
APLICACIONES:
Al aplicarse la fuerza al martillo apoyado éste sobre un punto O ; se produce un efecto de rotación (momento) que hace girar al martillo-clavo con respecto a dicho punto.
Al encontrarse demasiado duro el contacto del perno, es muy difícil extraerlo con una llave por mas grandiosa que sea la fuerza; por tal motivo se suele aumentar el brazo de palanca con ayuda de una barra.
La obtención de un momento de giro enorme con la ayuda de una palanca grande, condujo a Arquímedes a afirmar: “Dadme un punto de apoyo y moveré la Tierra”. Sin embargo lo que no tuvo en cuenta Arquímedes fue que la Tierra no está sola, sino que pertenece a todo un sistema ( el sistema solar, y éste a la vía láctea y éste al universo).
TEOREMA DE VARIGNON
Establece que la suma algebraica de los momentos producidos por un grupo de fuerzas con respecto a un punto cualquiera es igual al momento producido por la fuerza resultante respecto a dicho punto.
SEGUNDA CONDICIÓN DE EQUILIBRIO
" Si un cuerpo se encuentra en equilibrio, se cumple, que la suma de momentos de las fuerzas que actúan sobre él, con respecto a un mismo punto es igual a cero " ; es decir cuando un cuerpo sometido a varias fuerzas, no gira, se encuentra en equilibrio de rotación y se cumple que el momento resultante respecto del centro de giro, es nulo.
De esto podemos deducir que: Si el momento resultante, respecto del centro de giro, es cero, la suma de módulos de los momentos de fuerza horarios y de los momentos de fuerza antihorarios son iguales.
"Aquí no se considera el signo de los momentos"
Podemos observar que en ambos casos el cuerpo no experimenta cambios en su estado mecánico de rotación (reposo o movimiento con rotación uniforme)
EQUILIBRIO MECÁNICO
Es aquel estado mecánico en el cual se encuentra un cuerpo, presentando equilibrio de rotación y traslación.
Para que un cuerpo se encuentre en equilibrio , es necesario que cumpla con las 2 condiciones de equilibrio.
CUPLA O PAR DE FUERZAS
Es un sistema de 2 fuerzas paralelas; iguales en módulo y dirigidas en sentido contrario, cuando una cupla actúa sobre un cuerpo trata de proporcionarle cierto movimiento giratorio.
Se creerá que la suma de los momentos de las dos fuerzas respecto a un punto dado es cero; sin embargo, no lo es.
Aunque las fuerzas F no producen la traslación del sólido sobre el cual actúan, tienden a hacerlo girar.
EJEMPLOS :
☛ Para introducir el sacacorchos hay que aplicar un par de fuerzas para hacerlo girar e introducirlo en el corcho.
☛ Para hacer girar el volante de un auto , se aplica un par de fuerzas.
EQUILIBRIO ESTÁTICO DE UNA PARTÍCULA
Una partícula se encuentra en equilibrio relativo si la suma de todas las fuerzas que actúan sobre ella es cero; esto es: sumatoria de fuerzas es nula
Si el objeto se trata de una partícula, ésta es la única condición que debe satisfacerse para el equilibrio.
Esto significa que si la fuerza neta sobre la partícula es cero
La partícula permanece en reposo relativo (si originalmente estaba en reposo) o se mueve con velocidad constante (si originalmente estaba en movimiento).
EQUILIBRIO ESTÁTICO DE UN CUERPO RÍGIDO
Cuando las fuerzas están actuando sobre un cuerpo rígido, es necesario considerar el equilibrio en relación tanto a la traslación como a la rotación.
Por lo tanto, se requieren las condiciones siguientes:
I) La suma de todas las fuerzas debe ser cero (equilibrio de traslación)
II) La suma de todos los momentos de las fuerza con respecto a cualquier punto debe ser cero (equilibrio rotacional):
Las dos condiciones deben cumplirse simultáneamente para que el cuerpo se encuentre en equilibrio; si una falla, no hay equilibrio estático.
EQUILIBRIO Y REPOSO
Terminaremos este capítulo con una revisión de los conceptos de reposo y equilibrio.
☛ Una partícula se encuentra en reposo con relación a un observador inercial cuando su velocidad, medida por este observador es cero.
☛ Una partícula se encuentra en equilibrio con respecto a un observador inercial cuando su aceleración es cero.
Una partícula puede estar en reposo con relación a un observador inercial pero no estar en equilibrio.
EJEMPLO :
Cuando tiramos verticalmente hacia arriba la piedra, está momentáneamente en reposo cuando alcanza su altura máxima.
Si embargo no esta en equilibrio.
☛ Igualmente una partícula puede estar en equilibrio y no estar en reposo relativo a un observador inercial.
EJEMPLO :
En partícula libre, como no actúan fuerzas sobre ella, no hay aceleración y la partícula se encuentra en equilibrio.
La situación más común que se encuentra es aquella de una partícula que esta tanto en reposo como equilibrio al mismo tiempo.
Por dicha razón muchas personas consideran erróneamente los dos conceptos como sinónimos.
Por supuesto, una partícula en equilibrio puede estar siempre en reposo en algún sistema inercial de referencia.