MÉTODO DEL POLÍGONO EJERCICIOS RESUELTOS PDF
¿Qué es el método del polígono en vectores?
Este método es una generalización del método del paralelogramo, el cual resulta un caso particular.
Se emplea, sobre todo, cuando se desean sumar varios vectores a la vez.
En el extremo del primer vector se sitúa el punto de aplicación del segundo, sobre el extremo del segundo vector se coloca el punto de aplicación del tercero y así hasta terminar de dibujar todos los vectores.
El vector resultante es el que se obtiene al unir el punto de aplicación del primero con el extremo del último.
¡Para hallar el módulo R, debemos valernos de la geometría del polígono!
• Si los vectores forman un polígono cerrado, la resultante será nula.
• Para el caso en que el polígono resulte ser un triángulo, se cumple la ley de senos para los módulos de los vectores.
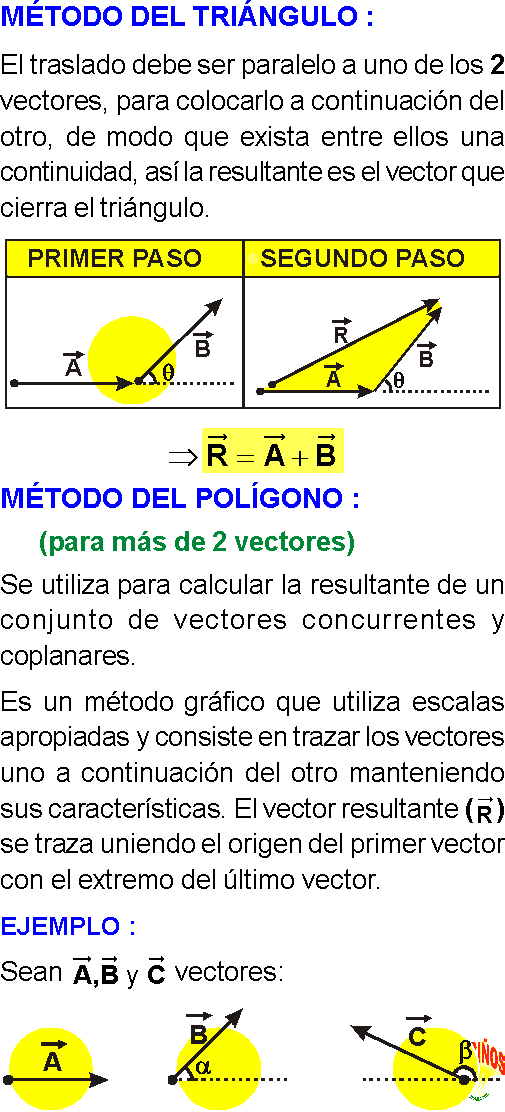
REGLA DEL TRIÁNGULO
El traslado debe ser paralelo a uno de los 2 vectores, para colocarlo a continuación del otro, de modo que exista entre ellos una continuidad, así la resultante es el vector que cierra el triángulo.
REGLA DEL POLÍGONO : (para más de 2 vectores)
Se utiliza para calcular la resultante de un conjunto de vectores concurrentes y coplanares.
Es un método gráfico que utiliza escalas apropiadas y consiste en trazar los vectores uno a continuación del otro manteniendo sus características.
El vector resultante se traza uniendo el origen del primer vector con el extremo del último vector.
Recuerda que todos los vectores no colineales ni paralelos no pueden sumarse directamente, puesto que la suma aritmética o algebraica es diferente a la suma vectorial en el caso de estos vectores.
Recuerda que el vector suma, o resultante vectorial, de 2 o más vectores no colineales ni paralelos, se determina ubicando los vectores uno a continuación de otro, determinando estos una poligonal abierta, que será cerrada por el vector resultante.
CASO ESPECIAL
Cuando el polígono presenta los vectores sucesivos, es decir no observamos intersección de cabezas de flecha, no existirá resultante
PARA VECTORES COLINEALES
Dos vectores tienen su Máxima Resultante cuando son paralelos y colineales y tienen su Mínima Resultante cuando son opuestos.
Lo anterior, también se cumple para más de 2 vectores colineales.